Review
Logistic regression
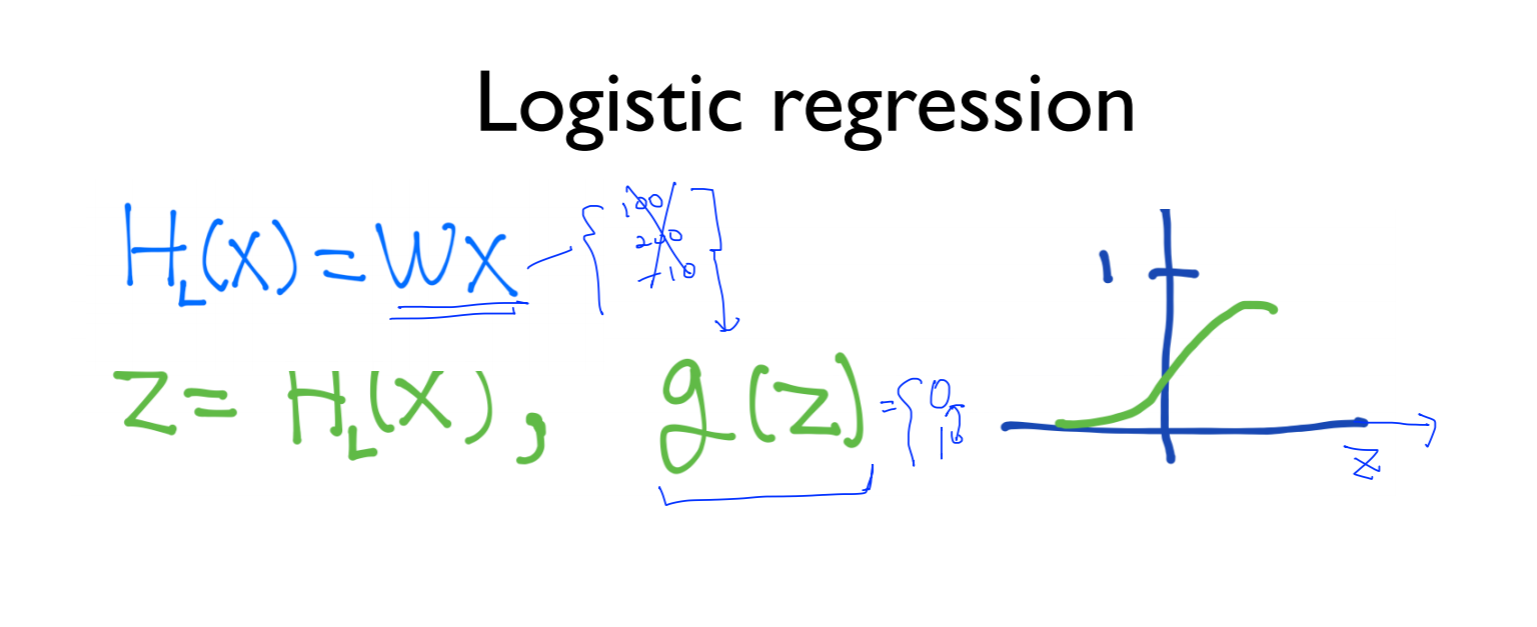
H(x)의 함수는 100, 200, -10 과 같이 큰 값의 결과를 얻어내기 때문에 z라는 압축된 수로 나타내길 원함
따라서 아무리 큰 값이더라도 0-1사이의 값으로 나타낼 수 있음
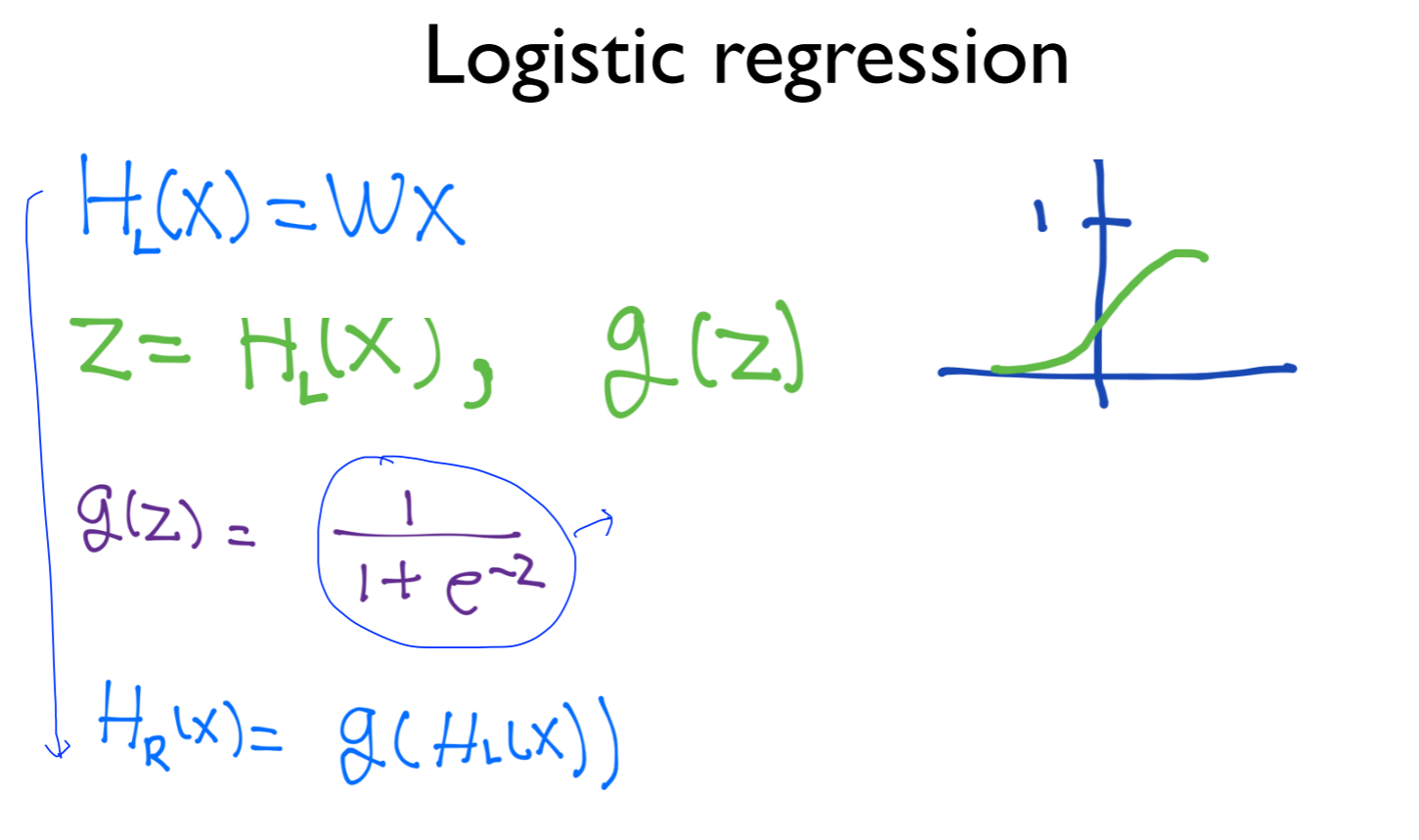
g(z)의 식은 다음과 같이 나타낼 수 있으며, 이 식을 sigmoid 또는 logistic function 이라고 부름
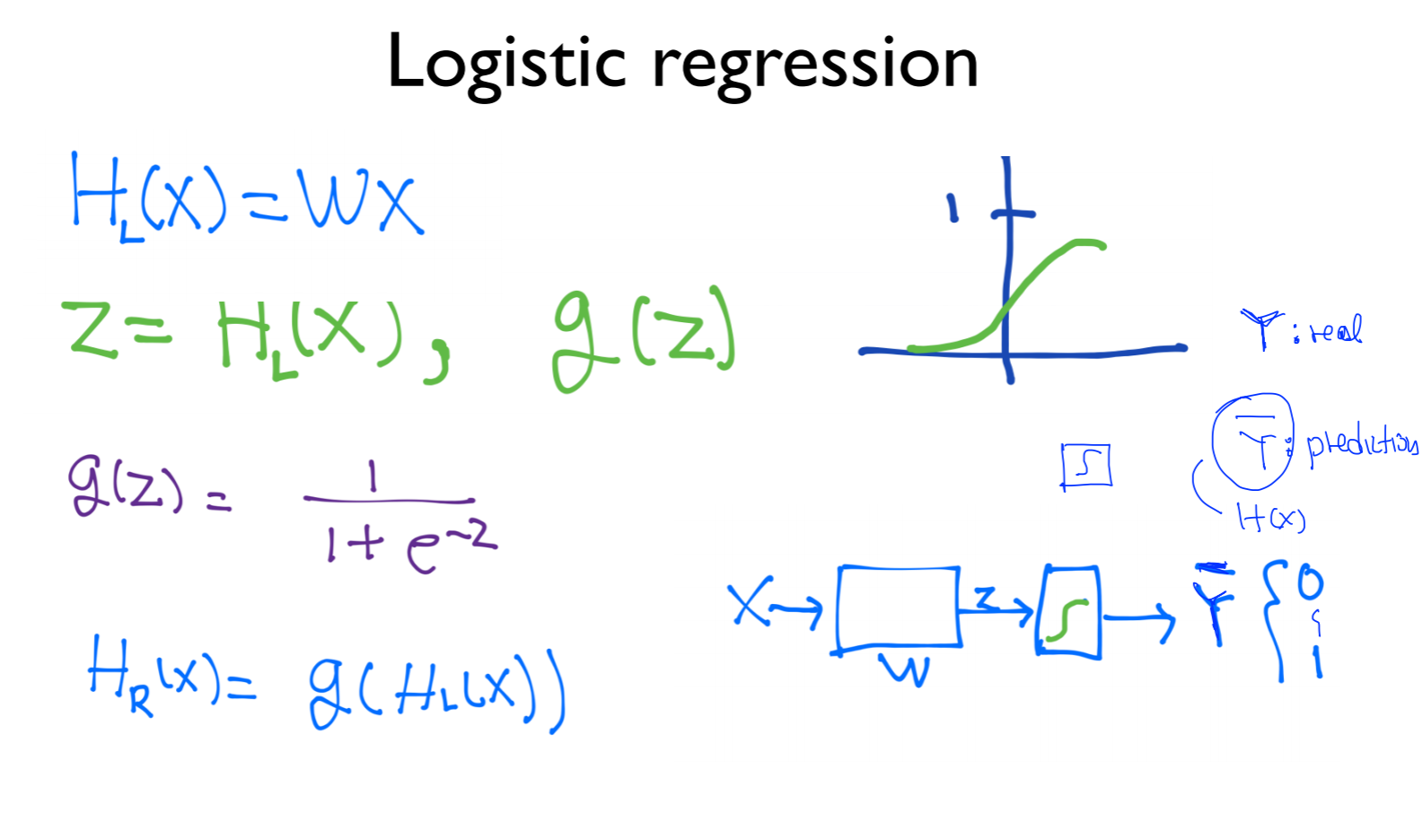
식을 그림으로 나타내면 위의 그림의 아래에 있는 그림으로 나타낼 수 있음
네모에 s 모양이 있는 것은 sigmoid 함수를 지나친다는 의미
Y: real
(Y) ̅: prediction (Y의 헷(?)) (= H(x))
의미함
logistic regression을 학습한다는 의미는 두가지의 분류를 구분하는 것을 의미함
위의 아이디어를 그대로 가져와서 multinomial classification을 할 수가 있음
Multinomial classification

x1: 공부한 시간
x2: 수업을 참여한 횟수
Y: 그에 따른 grade
각 A, B, C를 그래프로 그리면 오른쪽과 같이 나타낼 수 있음
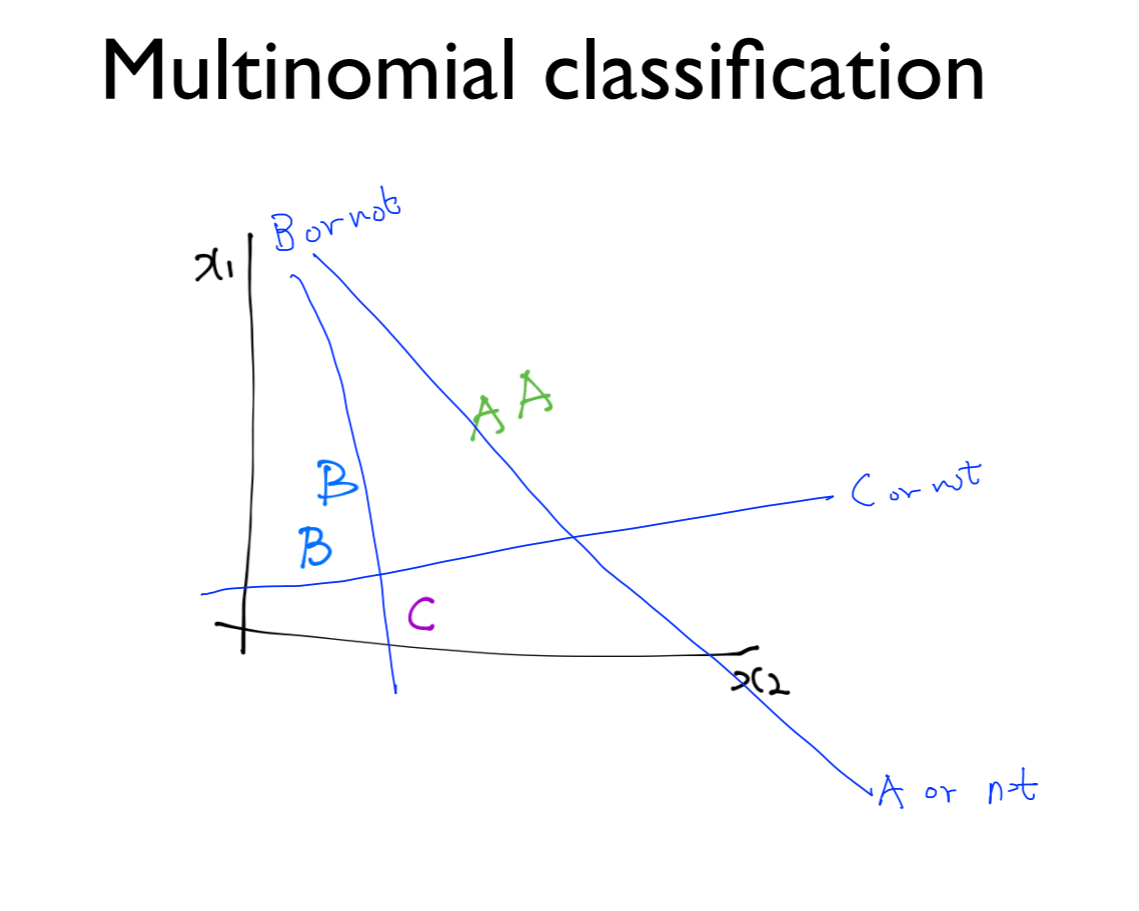
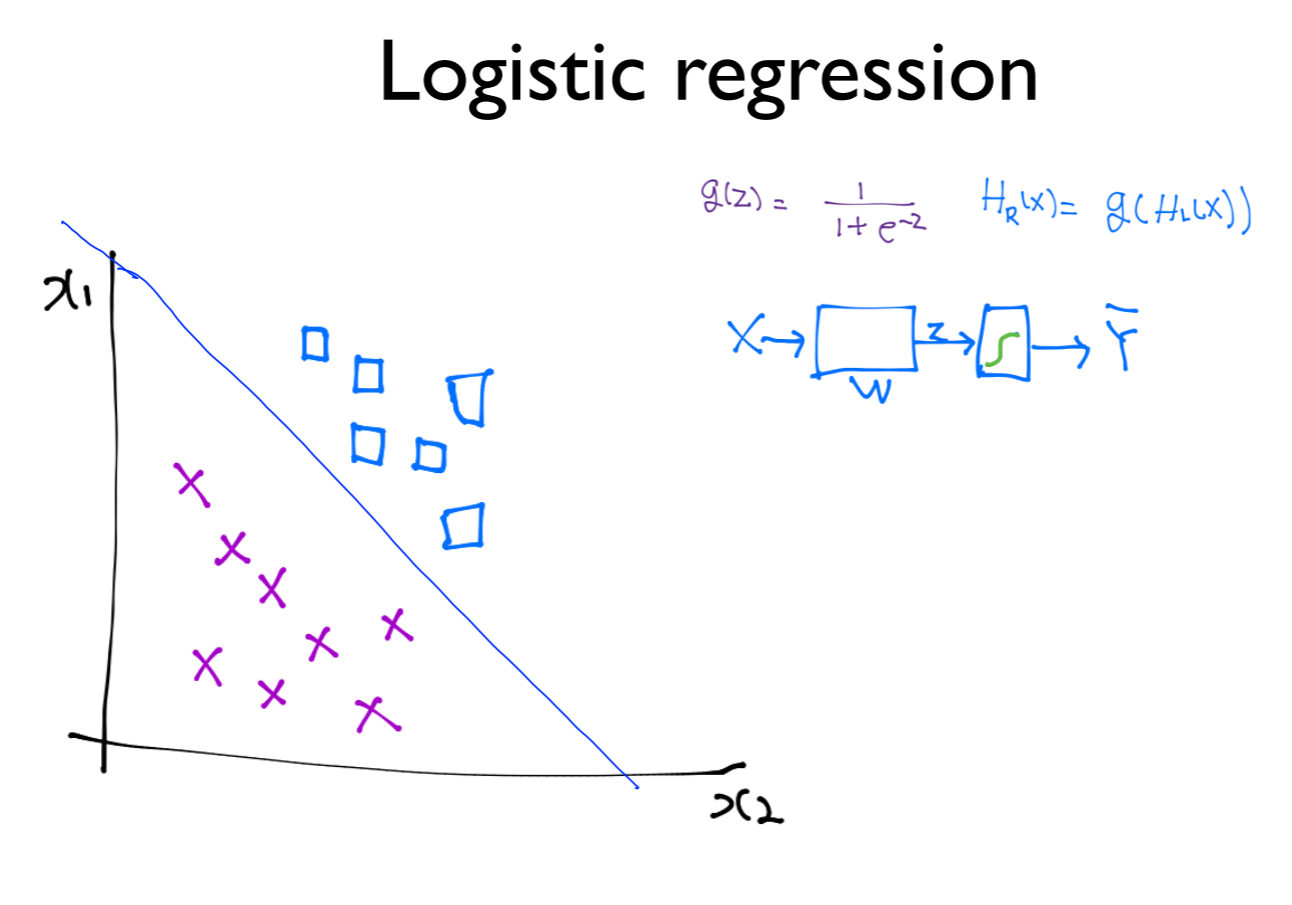
binary classification을 이용해서 구할 수 있음
하나는 C or not
또 하나는 B or not
또 다른 하나는 A or not
즉, 세 개의 각각 다른 binary classification으로 구현이 가능함

A인지 아닌지, B인지 아닌지, C인지 아닌지에 대한 예측함수를 파란색 그림과 같이 나타낼 수 있음
세 개의 독립된 classification을 구현할 수 있음
Hypothesis matrix

독립적으로 계산하면 위와 같이 나타낼 수 있지만,
각각이 독립이기 때문에 복잡함

그래서 연두색으로 써져있는 weight들을 쭉 밑으로 나열함
이것이 matrix multiplication 임
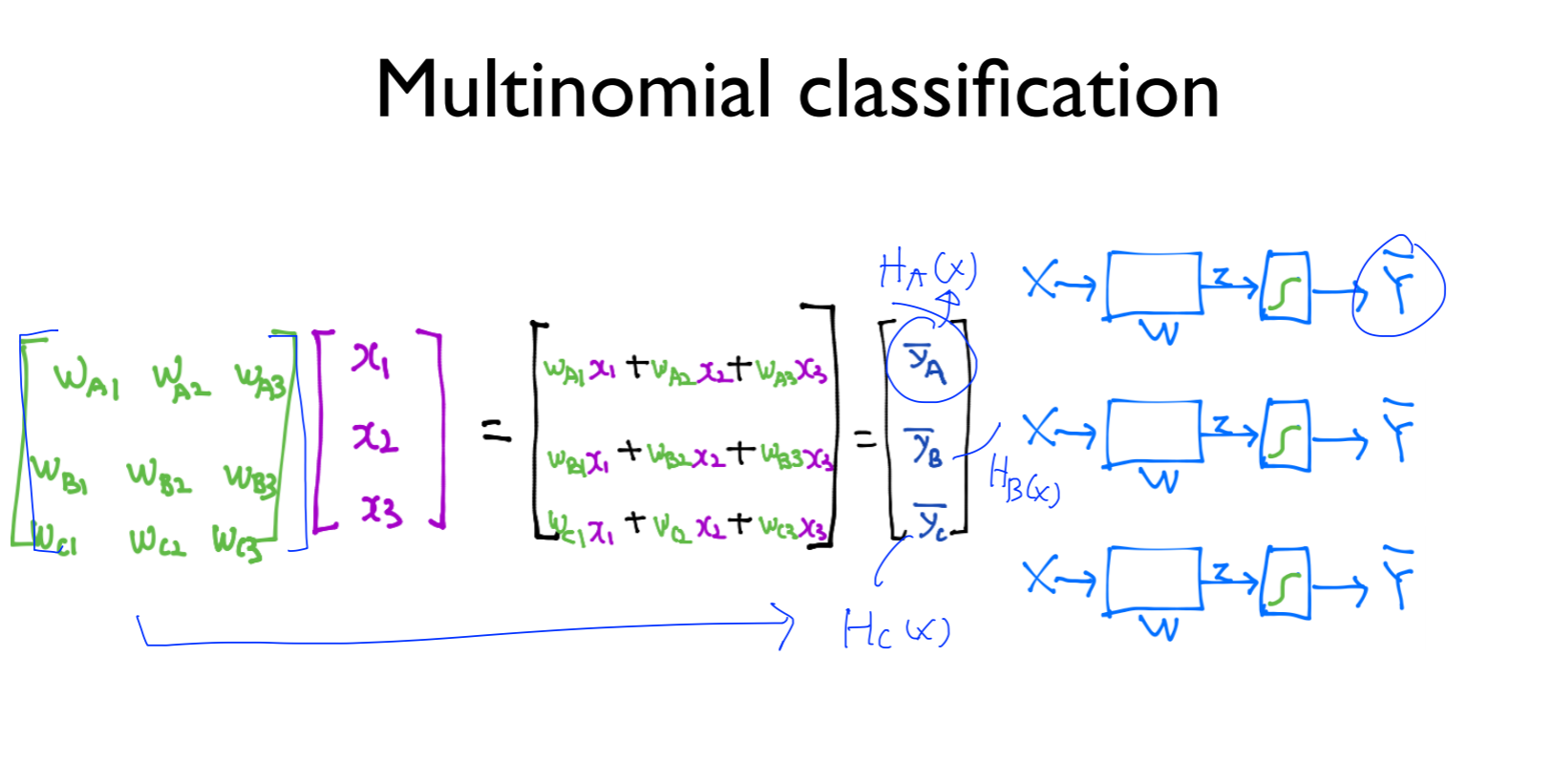
따라서 쭉 weight들을 작성하게 되면 matrix가 되고 이에 대한 matrix multiplication을 계산하면 각각의 독립된 (Y_A ) ̅, (Y_B ) ̅, (Y_C ) ̅ 를 얻을 수 있음. 이것은 각각 H_A(x), H_B(x), H_C(x) 임
where is sigmoid?
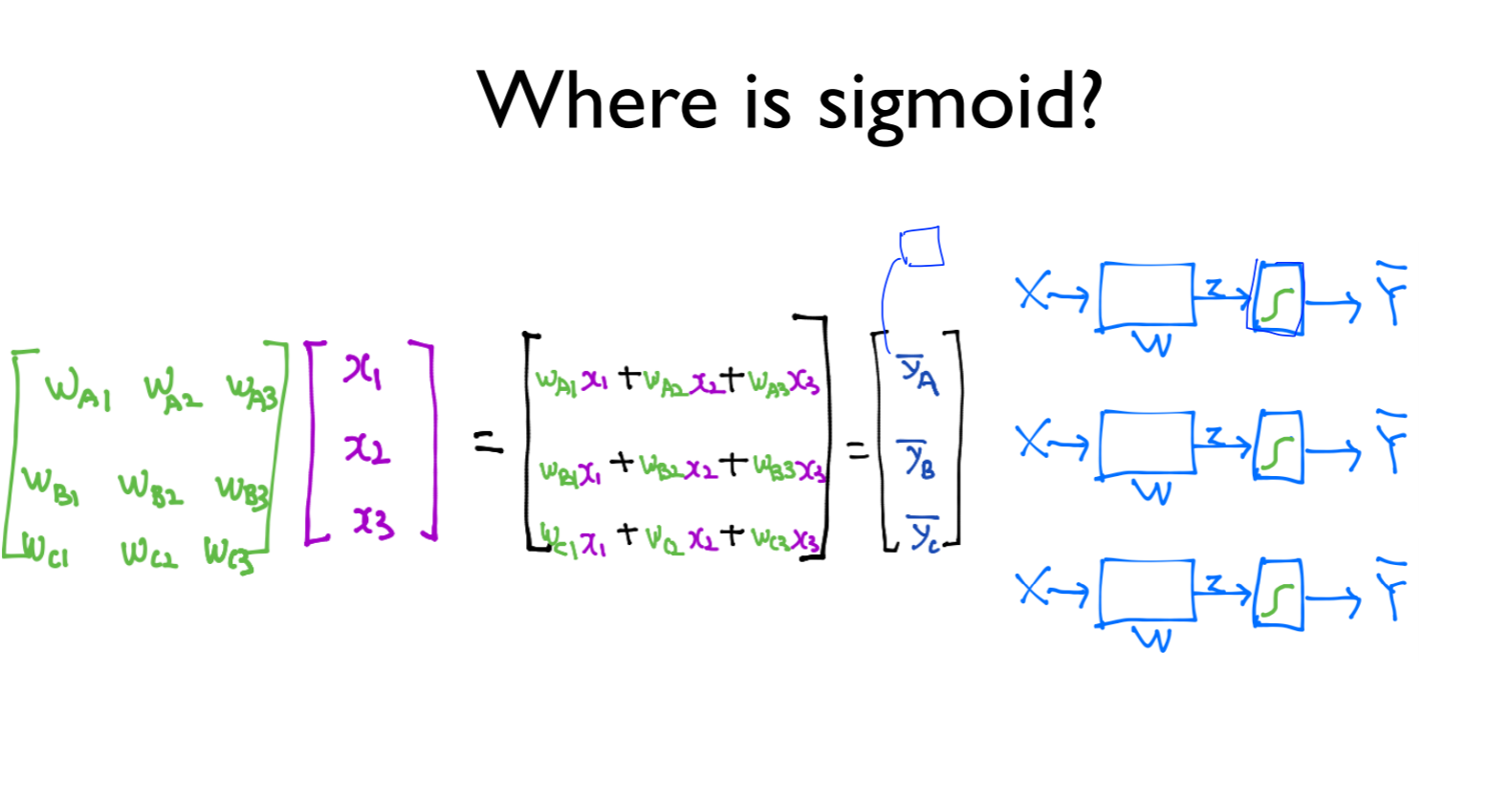
실수로 나오기 때문에 각각의 sigmoid를 처리해야함
이 내용은 다음 포스팅 참고
