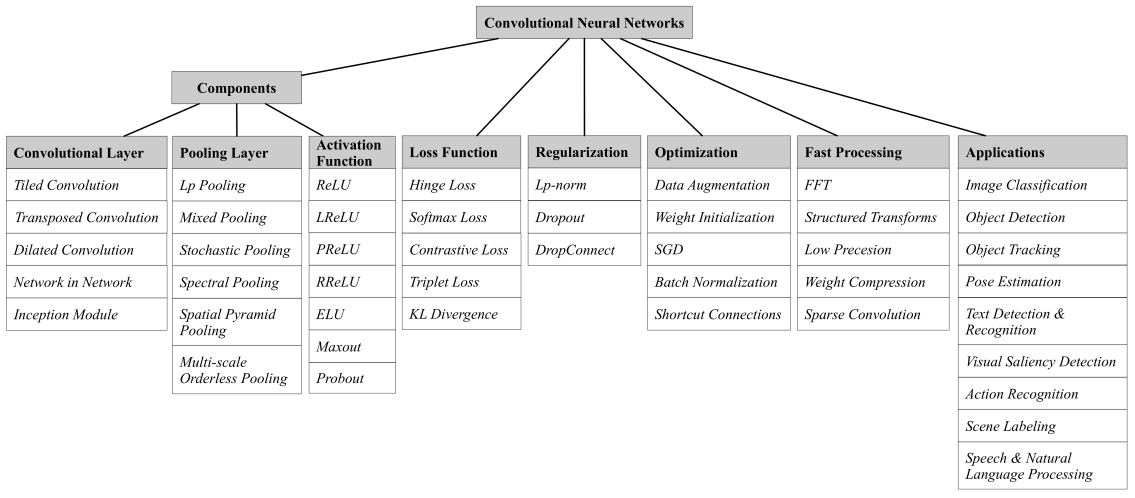
3.1. Convolution Layers
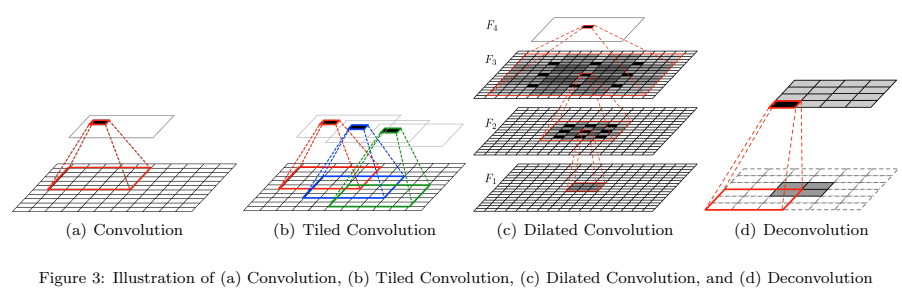
3.1.1 Tiled Convolution
Tiled CNN은 인접한 단위로 pooling함으로써 complex invariances을 학습하여, 인접한 은hidden units가 동일한 weights를 공유할 필요가 없음. 또한 learned parameter가 적다는 CNN의 장점이 있음
3.1.2 Transposed Convolution
이 논문에서는 'Deconvolution'이라는 용어를 사용하고 있는데, 기존의 convolution과 비교하여, Deconvolution은 single activation을 multiple output activation과 연관시킴. (d)는 unit stride와 zero padding을 사용한 4x4 input에 대한 3x3 operation을 보여줌.
Deconvolution은 먼저 padding으로 stride 값의 factor로 input을 upsampling 한 다음, upsampling된 input에 convolution 연산을 수행함
3.1.3 Dilated Convolution
Dilated Convolution은 최근 개발된 CNN으로, Conovlotional layer에 하나의 hyper-parameter를 더 도입함. Dilated Convolution은 필터 내부에 zero padding을 추가해서 강제로 receptive field를 늘리는 방법으로, (c)에서 검은 색 부분에만 weight가 있고, 나머지 부분은 0으로 채우짐. 이렇게 사용하는 이유는 해상도의 손실 없이 receptive field의 크기를 확장할 수 있기 때문에, 연산량 관점에서는 탁월한 효과를 얻을 수 있음
3.1.4 Network in Network
multilayer perceptron convolution (mplconv) layer에서, 전통적인 convolutional layer 다음에 1x1 convolutions을 배치함. 1x1 convolution은 ReLU에 의해 이어지는 cross-channel parametric pooling과 동일함. 따라서 mlpconv layer는 일반 convolutional layer의 계단식 cross-channel parametric pooling으로 간주할 수 있음.
결국, 최종 layer의 feature map을 공간적으로 평균화하는 global average pooling을 적용하고, output vector를 softmax layer로 직접적으로 공금함
Global average pooling은 Fully-connected layer와 비교하여, 더 적은 parameters를 갖기 때문에, overfitting의 위험성과 연산 부하를 감소시키는 효과가 있음
3.1.5 Inception Module
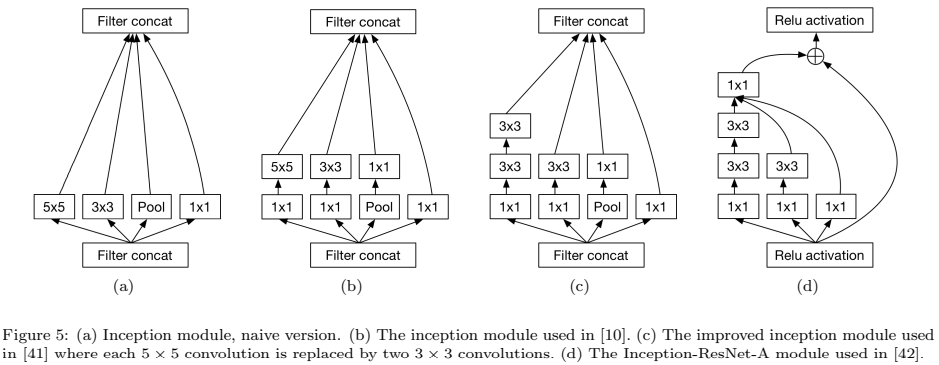Inception module은 하나의 pooling 연산과 세 가지 유형의 convolution 연산(그림 5(b))으로 구성되며, 1×1 convolution은 3×3 및 5×5 convolution 앞에 배치되어 계산 복잡성을 증가시키지 않고 CNN의 깊이와 폭을 증가시킴. Inception module을 통해 network parameter는 500만 개로 대폭 줄일 수 있음
ResNet에서 영감을 받은 최신 Inception-V4는 Inception architecture와 shortcut connection을 결합(그림 5(d))하여, shortcut connection이 네트워크의 훈련을 크게 가속화할 수 있다는 것을 발견함
3.2 Pooling Layer
3.2.1 Lp Pooling
Pooling은 Convolutional layers간의 연결 수(the number of connections)를 감소시킴으로써 연산량을 줄임
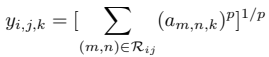
3.2.2 Mixed Pooling
복잡한 셀들에서 모델링된 생물학적으로 영감을 받은 pooling 프로세스로, Max pooling보다 더 나은 일반화를 제공함
max pooling과 average pooling의 결합으로 만든 mixed pooling method
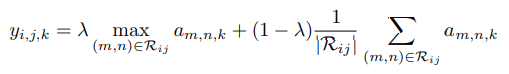여기서 는 average pooling과 max pooling을 선택하는 0 또는 1의 임의의 값으로, forward propagation 과정동안 는 기록되며, backpropagation 연산동안 사용됨
3.2.3 Stochastic Pooling
max pooling처럼 각 pooling 영역 내 최대 값을 선택하는 대신, stochastic pooling은 다항 분포에 따라 무작위로 activation을 선택하고, 이를 통해 non-maximal feature map의 activation이 사용되는 것 또한 가능하게 함
max pooling과 비교하여 stochastic pooling은 확률적인 성분에 의해서 overfitting을 피할 수 있음
3.2.4 Spectral Pooling
max pooling과 비교하여, spectral pooling의 linear low-pass fitering 연산은 동일한 출력 치수에 대한 더 많은 정보를 보존할 수 있다.
또한, 다른 pooling method에서 나타나는 output map dimensionality에서 급격하게 감소하지 않음. 게다가, spectral pooling의 과정은 메트릭스 절단(matrix truncation)에 의해 달성되며, 이는 convolution kernels에 FFT를 사용하는 CNN에서 적은 계산 비용으로도 구현될 수 있음
3.2.5 Spatial Pyramid Pooling
SPP(Spatial Pyramid Pooling)의 주요 장점은 input size에 상관없이 fixed-length representation을 생성할 수 있다는 것임. SPP는 이미지 크기에 비례하는 크기의 local spatial bins에 input feature map을 pooling하여 많은 fixted number of bins를 만듦.
이는 입력 크기에 따라 slinding windows의 수가 달라지는 이전 deep networks의 슬라이딩 윈도우 풀링과는 다름. 그들은 마지막 pooling layer를 SPP로 대체함으로써 다양한 크기의 이미지를 처리할 수 있는 새로운 SPP-net을 제안gka
3.2.6 Multi-scale Orderless Pooling
CNN의 discriminative power를 저하시키지 않고 invariance을 개선하기 위해 Multi-scale orderless pooling(MOP)을 사용함. 여러 scales의 전체 이미지와 로컬 patches 모두에 대해 deep activation features를 추출함. 전체 이미지의 activation는 global spatial layout 정보를 캡처하는 것을 목표로 하는 이전 CNN의 activation과 동일함. loacl patches의 activation는 invariance를 개선시키고, 이미지의 local, fine-grained detailes를 더 capture하는 것을 목표로 하는 VLAD 인코딩에 의해 종합됨
3.3 Activation Function
적절한 activation function은 특정 작업에 대한 CNN의 성능을 크게 향상시킴
3.3.1 ReLU
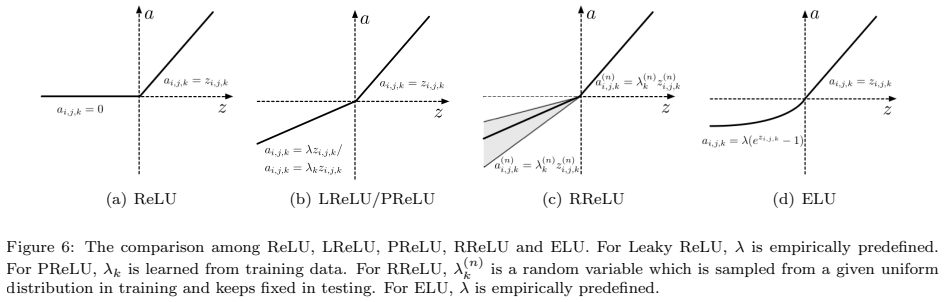
ReLU는 가장 주목할 만한 non-saturated activation의 하나로, 음수를 0으로 하고, 양의 부분을 유지하는 조각적 선형 함수(piecewise linear function)(그림 6(a)). ReLU의 간단한 최대(·) 연산은 sigmoid 또는 tahn activation function보다 훨씬 더 빠르게 계산할 수 있게 함. 또한 hidden unit에서 희소성을 유도하고 network가 sparse representations를 쉽게 얻을 수 있도록 함. 0에서 ReLU의 discontinuity는 역전파(backpropagation)의 성능을 저하시킬 수 있지만, 많은 연구는 ReLU가 sigmoid 및 tahn activation funtions보다 경험적으로 더 잘 작동한다는 것을 보여주었음
3.3.2 Leaky ReLU
ReLU의 잠재적인 단점은 unit이 활성화되지 않을 때마다 0의 기울기(gradient)를 갖는다는 것. 이는 gradient-based optimization이 weights를 조정하지 않기 때문에 초기에 활성화되지 않은 unit을 유발할 수 있음. 또한 constant zero gradients 때문에 training이 느려질 수 있음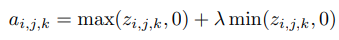
는 (0, 1) 범위의 predefined parameter. ReLU와 비교하여 Leaky ReLU는 음수를 상수 0으로 매핑하지 않고 압축하여 unit이 활성화되지 않았을 때 small, non-zero gradient를 허용함
3.3.3 Parametric ReLU
Leaky ReLU에 사전 정의된 parameter(λ)를 사용하는 대신 Parametric Rectified Linear Unit(PReLU) 정확성을 향상시키기 위해 Rectifiers의 parameters를 순차적으로 학습함.
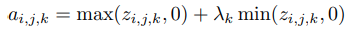는 k-th channel를 위해 학습된 parameter.
PReLU는 극히 적은 수의 extra parameters만을 도입하므로, 예를 들어 extra parameters의 수가 전체 network의 channel 수와 같기 때문에 overfitting 위험이 없으며 추가 연산 비용은 무시할 수 있음. 또한 backpropagation을 통해 다른 파라미터와 동시에 훈련할 수 있음
3.3.4 Randomized ReLU
Leaky ReLU의 또 다른 변형으로는 RReLU(Randomized Leaky Rectified Linear Unit). RReLU에서는 음수의 parameter가 training에서 균등 분포로부터 무작위 샘플링 됨(그림 6(c))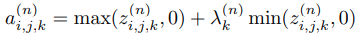
RReLU는 무작위 특성으로 인해 overfitting을 감소시킬 수 있음
3.3.5 ELU
ReLU, LReLU, PReLU 및 RReLU와 마찬가지로, ELU는 양수를 identity로 설정하여 gradient vanishing 문제를 방지함. ReLU와 달리 ELU는 빠른 학습에 도움이 되는 음수가 있음. 불포화 음수를 가지는 LReLU, PReLU 및 RReLU와 비교하여, ELU는 포화 함수를 음수로 사용함. 포화 함수(saturation function)은 비활성화 된 경우 units의 변화를 감소시키기 때문에 ELU를 noise에 더 robust하게 만듦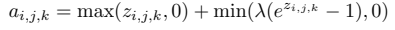
3.3.6 Maxout
Maxout은 각 공간 위치에서 여러 채널에 걸쳐 최대 반응을 취하는 대체 비선형 함수. ReLU는 사실 maxout의 특별한 경우이기 때문에, maxout은 ReLU의 이점을 모두 가지고 있음. 게다가 maxout은 Dropout과 함께 training 하기엔 매우 적합함
3.3.7 Probout
maxout에서의 최대 연산을 확률적 샘플링 절차로 대체함. Probout은 maxout units의 바람직한 특성을 보존하는 것과 invariance 특성을 개선하는 것 사이의 균형을 달성할 수 있음. 그러나 테스트 과정에서 확률 계산은 추가 확률 계산으로 인해 maxout보다 계산 비용이 많이 듬
3.4 Loss Function
3.4.1 Hinge Loss
SVM(Support Vector Machine) 같은 large margin classifier를 학습시킬 때 주로 사용함.
3.4.2 Softmax Loss
3.4.3 Contrastive Loss
3.4.4 Triplet Loss
3.4.5 Lullback-Leibler Divergence
3.5 Regularization
3.5.1 lp-norm Regularization
3.5.2 Dropout
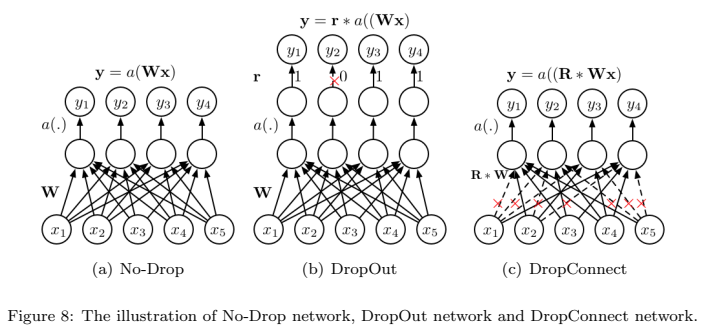
Dropout은 network가 neuron 중 하나 (혹은 neuron들의 small combination)이 너무 많이 의존하는 것을 방지하고, 특정 정보가 부재해도 정확해지도록 강제하는 역항르 함
Dropout을 개선하기 위해Gaussian 근사치를 sampling 하거나 binary belief network를 활용하여 각각 hidden variable의 dropout 가능성을 계산하는 adaptive dropout method를 제안함
3.5.3 DropConnection
DropConnection은 Dropout에서 한 단계 더 발전한 것으로, neurons의 출력을 0으로 random하게 하는 대신, DropConnection은 weight matrix 의 elements를 0으로 random하게 설정하는 것을 의미함
3.6 Optimization
3.6.1. Data Augmentation
Data augmentation은 data를 sampling, mirroring, roating, shifting, various photometric transformations을 통해 data가 가진 natures를 변경하지 않고 새로운 data로 변환하는 것을 의미함
3.6.2. Weight Initialization
training에서 빠른 수렴(convergence)를 달성하고 gradient vanishing을 방지하려면, 적절한 network initialization이 필요함
bias parameters가 0으로 초기할 수 있는 반면, weight parameters는 동일한 layer의 hidden units 사이에 대칭을 깨기 위해 신중히 초기화해야 함
3.6.3. Stochastic Gradient Descent
backpropagation algorithm은 parameters를 update하기 위해 gradient descent를 사용하는 standard training method임. 만흔 gradient descent optimization algorithm은 제안되었음
SGD의 각 parameter update는 single example과 반대로서 mini-batch에 대해 계산이 됨. 이렇게 하면 parameter update의 분산을 감소하고, 더 안정적으로 수렴하게 할 수 있음
그러나, mini-batch SGD는 좋은 수렴을 보장하지 않으며, 여전히 해결해야 할 몇 가지 문제들이 있음
적절한 learning rate를 선택하는 것이 어려움
초기 단계에서 안정적인 수렴을 주는 일정한 learning rate를 사용한 다음, 다음 수렴이 느려지면서 learning rate를 감소시키는 것이 일반적인 방법임
또한 SGD는 수렴을 초래하지 않을 수 있음. training 과정은 performance이 더 이상 개선되지 않으면 종료될 수 있음. over-training에 대한 일반적인 해결 방법은 training 중 validation set의 performance에 따라 optimization이 중지되는 것.
3.6.4. Batch Normalization
Normalization은 일반적으로 data preprocessing의 첫 번째 단계임. Global data normalization은 모든 data의 zero-mean, unit variance를 갖도록 변화시킴. 하지만 data가 deep network를 통해 흐를 수록, internal layer로의 입력의 분포가 변화되고, network의 학습 능력과 정확도를 잃게 됨.
BN(Batch Normalization)은 이러한 현상을 부분적으로 완화시킴.
training 전체 보다는 각각의 mini-batch를 연산한 후에 평균과 분산의 추정치가 연산되는 input layer에서 평균과 분산을 수정하는 normalization step을 통해 covariate shift 문제를 해결함
Global data normalization과 비교해서 BN은 많은 장점이 있음
먼저, internal covaiant shift를 감소시킴
둘째로, BN은 parameters의 초기값 또는 parameters의 scale에 대한 기울기 의존성을 감소시켜서, network를 통해 흐르는 gradient에 유익한 효과를 제공함. 이를 통해 발산(divergence)의 위험 없이 높은 learning rate를 사용할 수 있음.
또한, BN은 모델을 정규화(reqularize) 시키고, Dropout의 필요성을 감소시킴.
마지막으로, 포화 모델에 갇히지 않고, 포화 비선형 활성화 함수를 사용할 수 있음
3.6.5. Shortcut Connections
Deep CNNs는 정규화된 초기화와 BN에 의해 gradient vanishing 문제가 완화될 수 있음. 이러한 방법은 deep neural networks가 overfitting하는 것을 방지할 수 있지만, network를 optimizing하는 것을 어렵게 만들어서 얕은 네트워크보다 performance가 나쁘게 만들 수 있음.
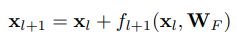
neroun-specifig gating을 위해 학습 가능한 weights를 가져오는 대신, ResNet의 shortcut connection은 gate가 되지 않고, 변환되지 않은 input이 바로 output으로 전파시켜서, 적은 parameter를 가져오도록 함
는 weight layer로, Convolution, BN, ReLU 또는 Pooling과 같이 연산희 복합 함수일 수 있음. residual block의 경우, 더 깊은 unit의 activation은 얕은 unit과 residual function의 activation의 합이라고 할 수 있음
이는 gradients가 직접적으로 얕은 unit에 전파되는 것을 의미하며, 이는 매우 깊은 network를 효과적으로 학습시킬 수 있고, original mapping function보다 deep ResNet을 더 최적화 시키기 쉽다는 것을 말함
이는 network가 깊어질수록 사라지는 일련의 metrix-vector products의 일박적인 feedforward networks와 대조적임
