[ICLR'25] MagicDec: Breaking the Latency-Throughput Tradeoff for Long Context Generation with Speculative Decoding

Hyunjoon Jeong·2025년 10월 11일

목록 보기

6/13

예전에 speculative decoding에 대한 글을 쓴 적이 있다. 아마 7월 쯤이였나? 그 때 조사하면서 알게 된 speculative decoding의 단점 중 하나가 batch size가 클 수록 효과가 떨어진다는 것이였다. 그러다가 이전 회사를 퇴사하고 지금 회사로 합류하면서, 팀장님이 이 논문을 추천해주셨다.

https://iclr.cc/virtual/2025/poster/30513

Speculative Decoding

LLM의 inference 단계는 두 가지로 나눌 수 있었다. 하나는 들어온 모든 input에 대해 KV 값을 생성하는 prefill 단계, 그리고 다른 하나는 이를 기반으로 토큰을 하나씩 생성하는 decoding 단계였다.

Speculative decoding은 LLM inference의 end-to-end latency에 가장 많은 시간을 차지하는 decoding 속도를 빠르게 하기 위해 고안 된 방법으로, 기존에 사용하려는 베이스 모델 앞에 작은 draft 모델을 두고, draft 모델이 토큰 후보를 생성하면 베이스 모델이 이를 검증하는 방식으로 decoding을 빠르게 수행하자는 것이 아이디어였다.

이전에 작성했던 speculative decoding은 아래 글에서 더 자세하게 작성했었다.

https://velog.io/@with1015/ICML23-Fast-Inference-from-Transformers-via-Speculative-Decoding

하지만 이 방식에는 batch size가 커질 수록 베이스 모델에서 발생하는 검증 비용이 증가하는 문제가 있었다. batch size가 커지게 되면 LLM은 memory-bound에서 compute-bound로 전환이 된다. 그렇기 때문에 draft 모델에서 생성 된 후보들을 검증하는 것에 많은 계산량을 소모해야 한다. 거기에 accept ratio까지 낮다면 잦은 reject으로 인해 더 많은 검증을 시행해야 한다.

Quantization, Pruning이나 KV cache eviction 같은 기법을 추가로 사용하면 큰 batch size에서도 throughput과 latency 개선이 가능하지만 문제는 LLM이 출력하는 결과물의 퀄리티가 떨어진다는 단점이 존재한다. speculative decoding이 주목을 받는 이유는 이러한 기법들에 비해 결과물의 퀄리티 감소 없이 decoding 단계에서의 latency가 감소하기 때문이다.

정확도 감소 없이 throughput과 latency를 개선하고, 큰 batch size와 긴 sequence에서도 먹히게 할 수 있을까?

Insights

MagicDec의 저자들은 3가지 insight를 기반으로 위와 같은 물음에 가능하다는 답변을 내렸다.

1. 긴 sequence + 큰 batch size 조합에서는 KV cache가 대부분의 병목을 차지한다.

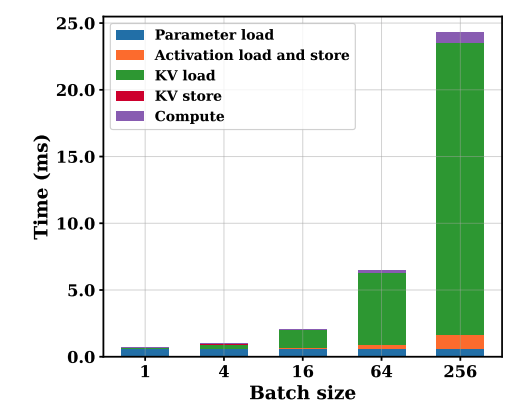
sequence length가 길고 그러한 sequence가 많이 모인 환경에서는 KV cache의 메모리 사용량이 모델 파라미터 보다 더 많은 공간을 차지하게 된다. 현대 GPU의 경우, 메모리 bandwidth에 비해 FLOPS가 크기 때문에 이러한 상황에서 LLM inference는 memory-bound 상태가 된다. 위 그래프는 LLaMA-3.1 8B 모델을 batch size를 늘려가면서 inference time breakdown을 시행한 결과이다. 저자들이 제시한 첫번째 insight에 따라 batch size가 커질수록 KV cache load/store에 많은 시간을 소모함을 알 수 있다.

2. Speculative decoding은 특정 임계 sequence 길이 이상에서는 KV cache 로딩이 대부분의 병목을 차지한다.

짧은 sequence의 경우, batch size를 늘리면 계산량에서 병목이 발생되어 검증 모델에서 이루어지는 inference가 비효율적이지만, 특정 임계 길이를 초과하면 KV cache의 로딩 비용이 대부분의 병목을 차지하게 된다. 이 시점 부터는 검증 계산의 오버헤드가 KV cache 로딩 비용에 비해 작아지게 되므로 speculative decoding이 효율적으로 동작하게 된다.

3. KV cache를 압축 시켰을 때 더 효율적인 inference가 가능하다.

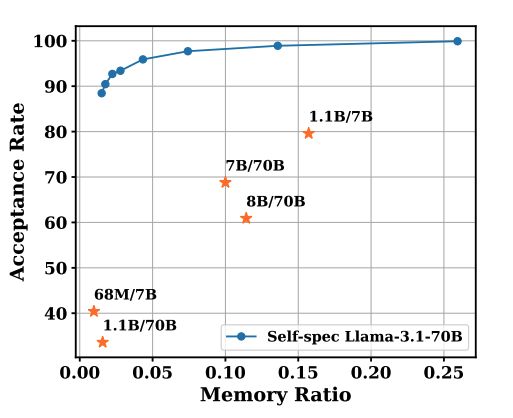
Speculative decoding의 성능을 결정하는 요소 중 하나는 acceptance rate이다. 이 값이 높을수록 draft 모델에서 만든 토큰 후보가 reject이 잘 이루어지지 않기 때문이다. 이 값을 향상 시키기 위해서 모델 파라미터를 압축 시키는 것에 비해 KV cache를 압축 시키는 것이 더 효과적이라고 주장한다.

위 그래프는 LLaMA-3.1 70B 모델에 대해 acceptance rate를 비교한 값이다. x축은 파라미터가 압축 된 draft 모델의 메모리 사용량이 베이스 모델 대비 어느 정도인지를 나타낸다. self-spec은 top-K 기반의 KV sparsification이 적용 된 것으로, KV cache가 압축 된 모델을 의미한다. 위 그래프 상으로 보았을 때, 동등한 메모리 제약에서 KV cache 압축은 90%에 준하거나 그 이상의 acceptance rate를 보여주었다.

Speculative Decoding의 성능 향상 조건

우선 speculative decoding에서 한 번의 검증 단계에서 발생 할 수 있는 기대 생성 토큰 수의 근사를 다음과 같이 정의 할 수 있다. ( $\alpha$ 는 acceptance rate, $\gamma$ 는 speculation length이다.)

E[generated\ tokens]=\frac{1-\alpha^{\gamma+1}}{1-\alpha}

그리고 speculative decoding 한 스텝에서 소요 되는 시간은 draft 모델이 decoding을 하는데 걸리는 시간과 베이스 모델이 검증하는 시간의 합을 이용하여 다음과 같이 구할 수 있다. ( $B$ 는 batch size, $S$ 는 sequence 길이를 나타낸다.)

T_{total} = \gamma \times T_{draft}(B, S) + T_{eval}(B, S, \gamma)

위 두 수식을 조합하면 다음과 같이 토큰당 평균 inference latency를 정의 할 수 있다.

T_{avg} = \frac{T_{total}}{E[generated\ tokens]}

그리고 위 식으로부터 speculative decoding의 속도 향상 비율을 구할 수 있다. 여기서 $T_{base}$ 는 베이스 모델이 decoding을 수행하는데 걸리는 시간을 의미한다. ( $T_{eval}$ 과 헷갈리지 말도록 하자.)

\frac{T_{avg}}{T_{base}}=\frac{1}{E[generated\ tokens]} \times (\frac{\gamma T_{draft}}{T_{base}}+\frac{T_{eval}(\gamma)}{T_{base}})

그렇다면 $T_{base}$ 에 비해 $T_{avg}$ 가 작아져야 speculative decoding을 적용했을 때 효과가 있는 것이니까, 높은 속도 향상을 위한 조건을 3가지로 요약 할 수 있게 된다.

베이스 모델의 decoding 비용 대비 검증 시간의 비율이 작아야 한다. 즉, $\frac{T_{eval}(\gamma)}{T_{base}}$ 값이 1에 근접해야 좋다.
베이스 모델의 decoding 비용 대비 draft 시간의 비율이 작을 수록 좋다. 즉, $\frac{ T_{draft}}{T_{base}}$ 값이 0에 근접해야 좋다.
$E[generated\ tokens]$ 은 클수록 좋다.

Sequence 길이와 Batch Size에 따른 성능 향상

앞에서 언급하였듯이 MagicDec에서는 짧은 sequence 길이를 사용 할 때, batch size가 커지게 되면 compute-bound로 전환이 된다. 그 이유는 LLM의 linear layer가 원인인데, batch size가 커질수록 arithmetic intensity가 증가하기 때문이다. 이로 인해 speculative decoding 입장에서는 후보 토큰의 병렬 검증을 위한 계산 리소스가 줄어들게 되고 결국 검증 비용이 높아지게 되는 것이다.

반면 중간이나 긴 sequence는 memory-bound로 전환이 된다. batch size가 커지면 KV cache의 로딩 비용이 대부분을 차지하게 되고, 이로 인해 검증 비용과 decoding 비용이 거의 비슷해진다. (앞서 언급한 1번 조건인 $\frac{T_{eval}(\gamma)}{T_{base}}$ 값이 1에 근접하는 상황이 만들어진다.)

특히 최신 GPU는 FLOPS에 비해 메모리 bandwidth가 낮은 편이기 때문에 batch size 크기가 증가해도 계산 시간보다 KV cache 로딩에 더 많은 시간을 사용하게 된다. 그래서 검증 연산의 비용이 증가하긴 하지만 KV cache가 일으키는 병목으로 인해 상쇄가 가능하다.

위와 같은 bottleneck shift를 기반으로 $S_{inflection}$ (임계 sequence 길이) 정의가 가능하다. 이 길이를 넘기는 sequence를 추론하는 speculative decoding은 batch size가 커져도 속도 향상이 더 커지는 경향을 볼 수 있다.

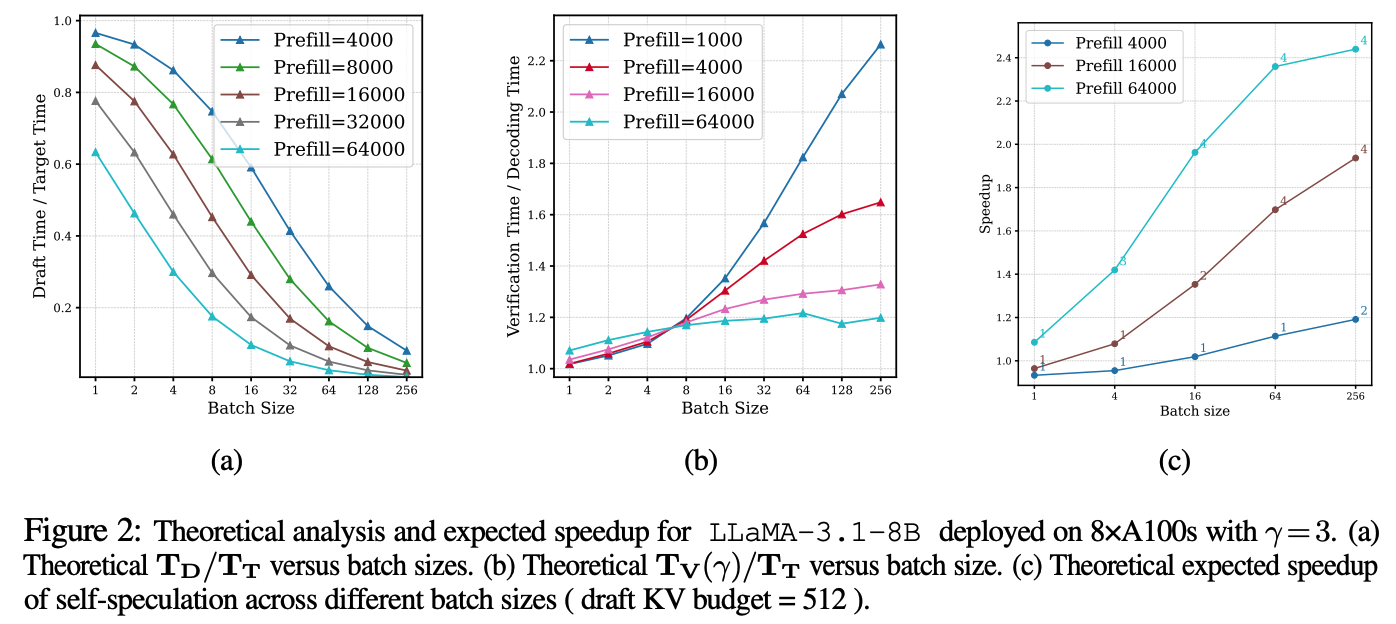
위 그래프, 특히 (c) 그래프에서 볼 수 있듯이 LLaMA-3.1 8B의 경우, $S \ge 4000$ 부터 batch size가 클수록 속도 향상이 증가하는 것을 볼 수 있다. 이 $S_{inflection}$ 값은 모델 아키텍쳐나 하드웨어 구성, 또는 draft 방식에 따라 값이 달라지게 된다. 예를 들어 높은 FLOPS에 비해 낮은 메모리 bandwidth를 가지는 경우 더 작은 $S_{inflection}$ 값을 가지게 된다. 또한 LLaMA-3.1 8B는 GQA (Grouped Query Attention)을 사용하는데, 이로 인해 KV memory footprint가 크기 때문에 동일 조건에서 더 큰 $S_{inflection}$ 값을 가진다.

정리하자면 sequence 길이 $S$ 와 $S_{inflection}$ 관계는 다음과 같다.

(1) $S \lt S_{inflection}$

batch size가 커질수록 compute-bound가 됨
계산 자원이 포화 상태가 되기 때문에 검증 비용이 크게 증가함

(2) $S \ge S_{inflection}$

KV cache 로딩이 주요 병목이 되면서 memory-bound가 됨
베이스 모델 디코딩 시간에 비해 검증 비용이 작아짐
draft 모델의 디코딩 시간 또한 베이스 모델에 비해 작아짐

KV Cache Compression

MagicDec에서는 draft 모델을 베이스 모델을 경량화 시켜서 사용하는 것에 비해 KV cache를 압축하여 draft 모델로 사용하는 것이 더 효율적이라고 주장한다. 그 이유로 두 가지를 제시했다.

1. KV cache 크기는 모델 파라미터 메모리보다 크다.

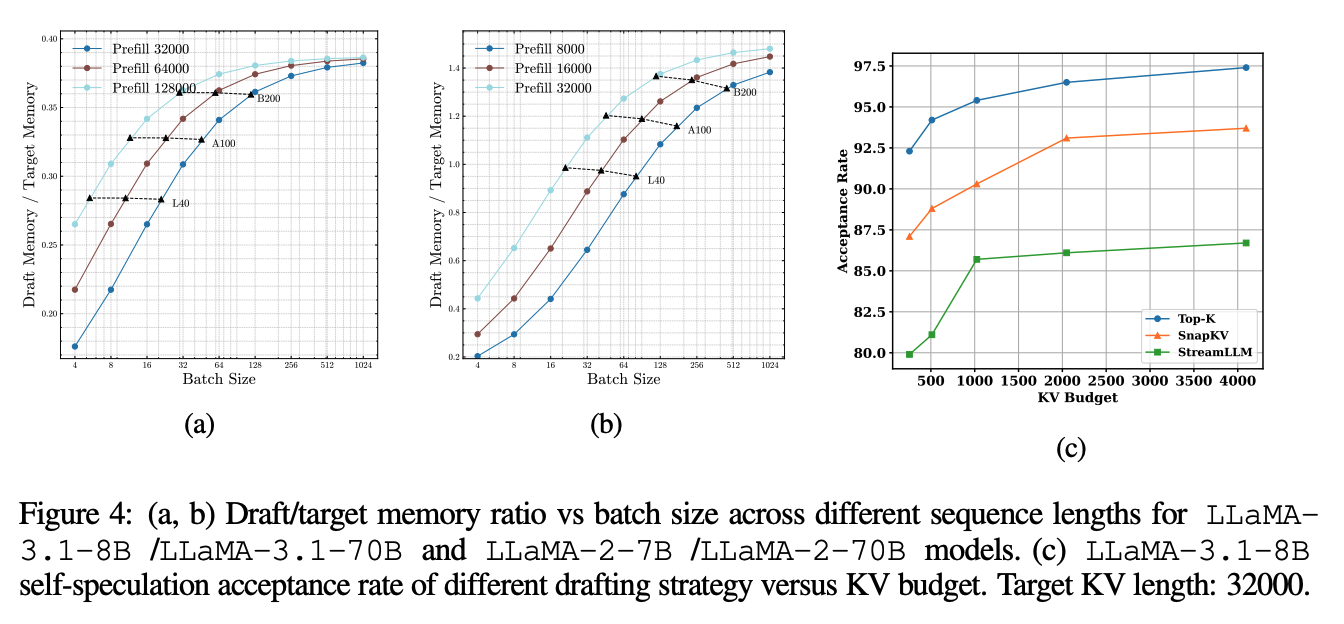
위 그래프 (a)와 (b)는 각각 LLaMA-3.1 70B의 draft 모델로 8B를 사용하거나, LLaMA-2 7B를 사용한 그래프이다. batch size가 커질수록 베이스 모델에 비해 draft 모델의 메모리 footprint가 38~140%까지 팽창하는 것을 볼 수 있다.

이는 일반적으로 모델의 dimension에 비해 KV cache의 dimension이 더 크기 때문이고, 이로 인해 작은 draft 모델만으로는 부족하다는 것을 증명한다. 그렇기 때문에 앞서 언급한 KV cache를 압축 시켜서 이를 기반으로 draft를 시키는 것이 더 효율적이라고 주장한다.

2. KV cache 압축 모델이 더 높은 acceptance rate를 달성했다.

두 번째로는 KV cache를 압축 시켜서 draft 시킨 것이 모델을 경량화 하여 사용한 것보다 acceptance rate가 더 높게 발생했다는 것이다. 앞서 수식에서 증명하였듯이 acceptance ratio가 커지면 기대 할 수 있는 토큰의 양이 많아지고, 이로 인해 베이스 모델에서 검증이 덜 발생하게 된다. 이에 대한 내용은 뒤에 실험 부분에 더 보충이 되어 있다.

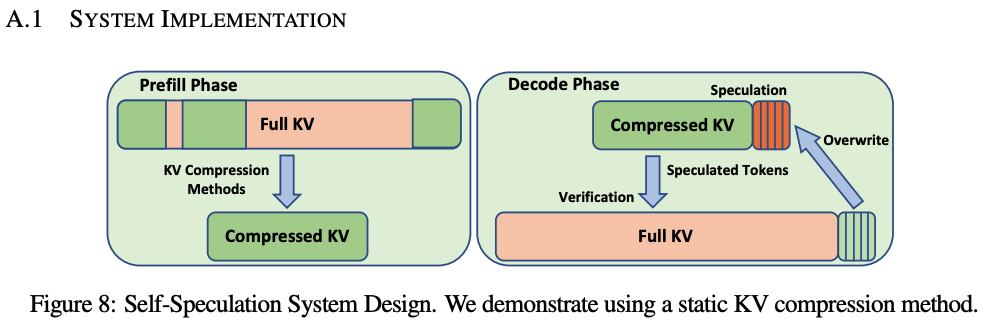
MagicDec

MagicDec의 디자인은 위 그림과 같다. KV cache는 static 방식으로 압축이 되고, 이는 LLM의 prefill 단계에서 생성이 되고, draft 과정에서 사용 된다. 위 그림을 기반으로 GPT-Fast라는 inference backend 위에 구현을 했고, attention은 FlashInfer를 사용했다고 한다.

KV cache 압축을 적용한 Speculative decoding 성능 향상 수식 증명

MagicDec에서 KV cache 압축을 이용한 draft 방식을 효율적으로 사용하기 위해서는 고려해야 할 3가지가 있다. 이를 종합적으로 고려하여 draft cost와 acceptance rate 사이에서 발생하는 trade-off의 최적값을 찾을 수 있다.

draft 모델의 크기
draft 모델의 KV cache 크기 및 KV budget
KV cache 압축 알고리즘

이 3가지 요소를 적용하기 전에, 이전에 증명한 speculative decoding 성능 향상 수식으로부터 KV cache 압축을 적용 했을 때의 일반적인 성능 향상 수식을 이끌어내야 한다. MagicDec에서 보여준 방식은 sparse KV selection 알고리즘을 이용한 KV cache 압축이다. 물론 다른 방식을 적용하여 확장도 가능하다고 한다.

sparse KV selection 알고리즘을 적용하였을 때, draft 모델에서 발생하는 비용은 draft 모델의 decoding에 발생하는 비용과 KV 선택 비용의 합으로 이루어진다. KV budget을 $K$ 라고 정의 하면, 다음과 같이 정의 할 수 있다.

T_{D, select}(B, S) = T_{draft}(B, K) + T_{select}(B, S, K)

이를 이전에 유도 했던 speculative decoding 성능 향상 수식에 draft decoding 자리에 그대로 대입하면 최적화 목표 식을 다음과 같이 유도 할 수 있다.

\min [\frac{T_{avg}}{T_{base}}] = \min [\frac{1}{E[generated\ tokens]} \times (\frac{\gamma \times (T_{draft}(B, K) + T_{select}(B, S, K))}{T_{base}}+\frac{T_{eval}(\gamma)}{T_{base}})]

결국 위 수식으로부터 보여야 할 것은, $T_{base}$ 나 $T_{eval}$ 과 관련 된 값들은 베이스 모델의 값이기 때문에 고정이 되므로, $T_{draft}$ 를 나타내는 draft 모델의 크기, $K$ 값을 나타내는 KV budget, 그리고 $T_{select}$ 를 나타내는 KV cache 압축 알고리즘이다.

Draft 모델 크기 선택

KV cache 압축을 하더라도 draft 모델 자체의 성능은 여전히 중요하다. 만약 KV cache 크기가 작은 경우에는 모델 파라미터를 로드 하는 비용이 draft 비용에 큰 비중을 차지한다.

batch size가 작은 경우, 보통 KV cache를 압축한 모델이 베이스 모델 대비 draft decoding 비용이 낮다. 이 경우, self-speculation보다 더 좋은 성능을 가질 수 있다.
sequence 길이까지 작은 경우, 모델 파라미터 로드로 인해 draft 성능이 낮아진다. 또한 acceptance rate 조건이 낮아지기 때문에 더 가벼운 draft 모델을 사용 할 수 있다.
일정 batch size 크기가 넘어가면 self-speculation이 더 높은 acceptance rate를 주기 때문에 다른 방식에 비해 더 효율적으로 동작하게 된다.

KV Budget 값 선택

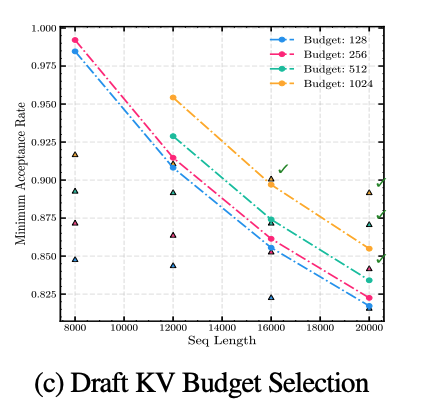
최적의 KV cache 크기는 batch size와 LLM에서 사용하는 sequence 길이에 따라 달라진다. 그래서 우선 최적 KV cache 압축 알고리즘을 결정하기 전에 KV cache 메모리로 사용 할 수 있는 시스템의 메모리 budget부터 결정해야 한다.

위 그래프는 self-speculation에서 static KV cache 선택 알고리즘을 사용 할 때, batch size와 sequence 길이에 따라 발생하는 최소 acceptance rate를 보여준다. KV budget과 draft 모델이 다르면 이러한 draft 비용 대비 acceptance rate 그래프는 당연히 다른 양상을 보이게 된다.

또한 MagicDec은 동일한 batch 안에서도 sequence마다 다른 draft KV cache를 적용 시킬 수 있다고 한다.

KV select strategy

마지막으로 고려해야 할 것은 KV를 선택하는 알고리즘 중 어떤 것을 사용할 것인가에 대한 점이다. 이 때 생각해야 하는 것은 KV 선택을 위한 비용인 $T_{selelct}$ 이다. 논문에서는 그 예시로 top-K attention을 들었는데, 이 방식은 들어가는 KV budget도 적지만 높은 acceptance rate를 보여준다고 한다. 하지만 이 방식의 단점이 $T_{selelct}$ 가 높아서 실제로 draft 방식으로 쓰기에는 부적절하다.

보통 KV select 알고리즘은 static 방식과 dynamic 방식으로 정리 된다. 각각의 특성은 아래와 같다.

Static KV selection
사전에 sparse KV cache를 만들어서 탐색으로 인한 오버헤드를 제거한다.
대신 acceptance rate가 상대적으로 낮다.
Dynamic KV selection
sequence마다 KV cache를 검색하여 top-K의 근접 항목을 찾는다.
acceptance rate가 높지만 탐색 오버헤드가 매우 크다.

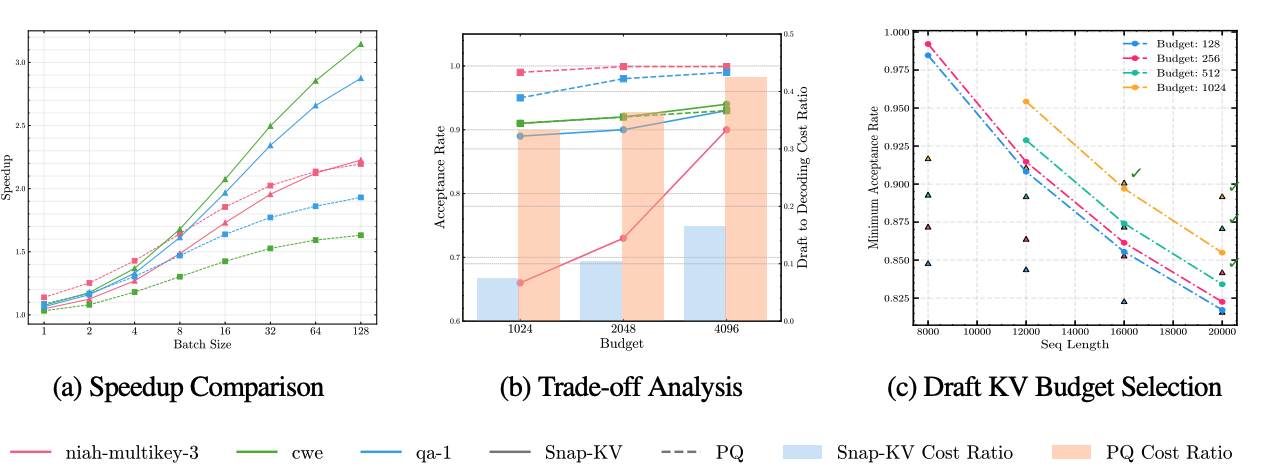
두 방식 모두 장단점이 존재하기 때문에, 적절한 방식을 선택하기 위해서 LLaMA-3.1 8B 모델에서 self-speculation 실험을 진행하였다. (b) 그래프를 살펴보면, static 방식인 Snap-KV와 dynamic 방식인 PQCache를 3가지 워크로드에서 각각 비교하였다.

두 방식이 만약 acceptance rate가 동일하다면 static 방식이 더 우세하였다. 반면 acceptance rate가 1에 가까워질수록 dynamic 방식이 더 긴 speculation length를 사용 할 수 있다. 하지만 batch size가 커질 수록 KV 탐색 비용도 커지고, 이 오버헤드가 대부분의 실행 시간을 차지하기 때문에 높은 batch size에서는 static 알고리즘이 더 효율적이다.

실험 결과

MagicDec이 높은 batch size와 긴 sequence 길이에서도 speculative decoding으로 latency 개선이 가능하다는 것을 보이기 위해서, 실험에서는 LLaMA-3.1 8B와 PG-19라는 데이터셋을 사용하여 실험을 진행했다.

draft 방식은 StreamingLLM이라는 sparse KV cache를 이용하였고 이는 static한 KV 선택 방식에 속한다. 그리고 KV budget을 조정해가면서 draft 비용과 acceptance rate 사이의 trade-off까지 분석했다고 한다.

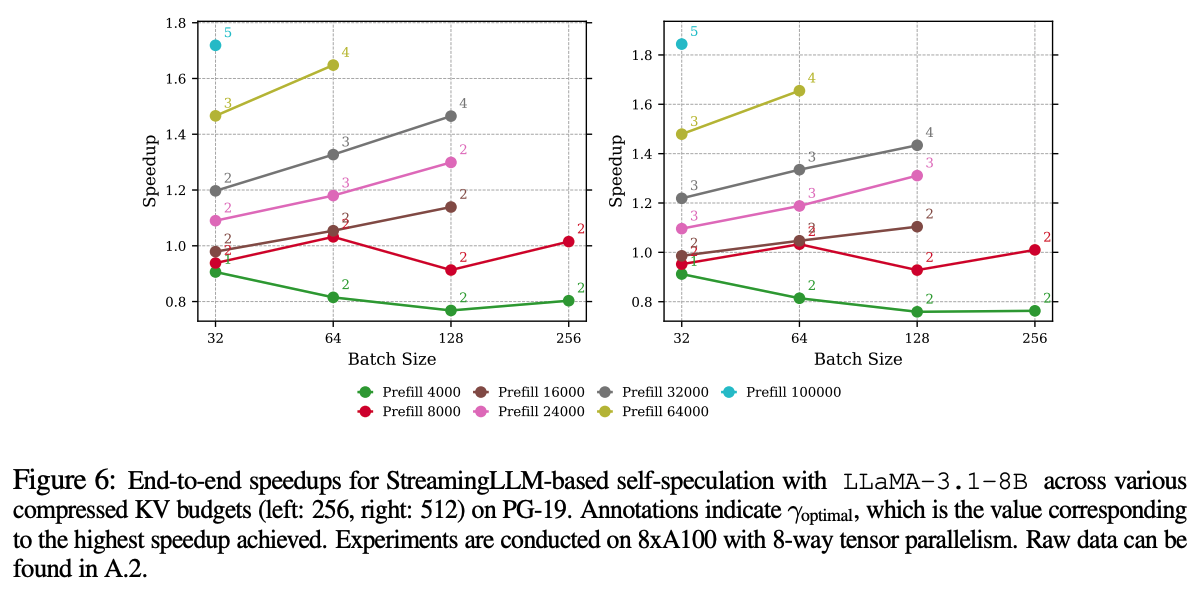
위 그래프는 다양한 batch size와 sequence 길이에 대한 최적의 speculation length에서의 속도 향상을 나타낸 그래프이다. 왼쪽은 KV budget을 256을 사용했고, 오른쪽은 512를 사용했다. 높은 batch size에서 10000 이상의 긴 sequence들은 성능 향상이 일어났지만, 그 이하의 길이에서는 오히려 성능이 낮아졌다.

추가로 이 실험에서는 draft 모델의 KV budget에 따른 성능을 볼 수 있다. batch size가 커질수록 그리고 sequence 길이가 클 수록 더 큰 KV budget에서 더 높은 속도 향상을 보여준다.

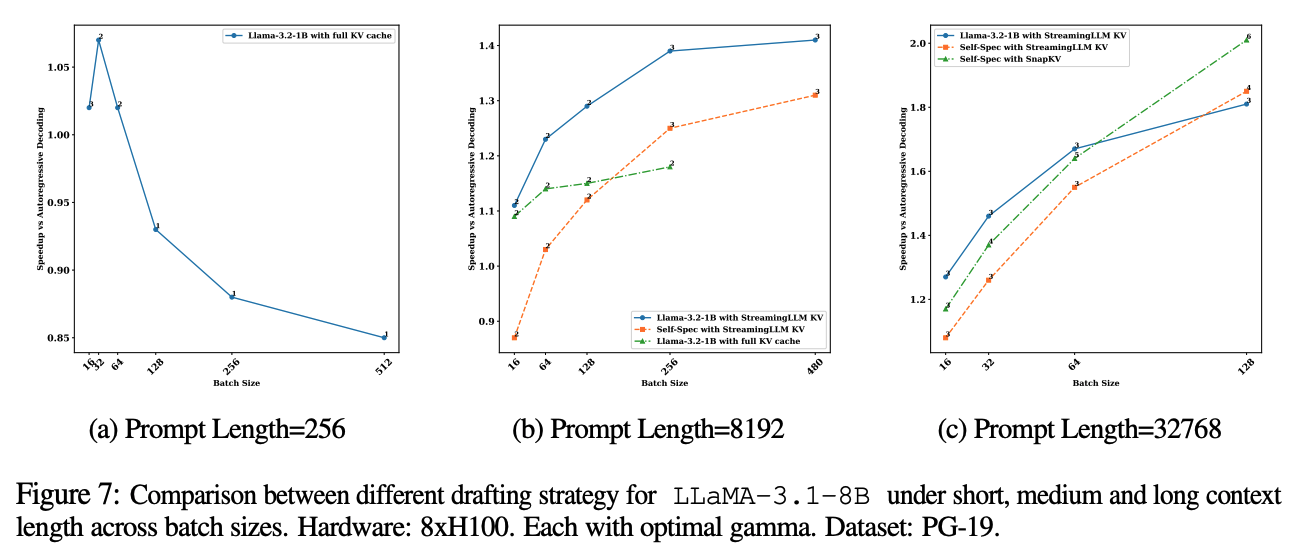
위 그래프 중 (b)와 (c)는 StreamingLLM 기반과 SnapKV 기반의 static KV cache 압축 방식을 비교했다. StreamingLLM에 비해 SnapKV가 더 뛰어난 성능을 보였다. 두 방법 모두 KV cache 탐색으로 인한 오버헤드는 없지만 SnapKV의 acceptance rate 증가율이 KV budget에 따라 빠르게 증가하기 때문이였다.

다양한 길이의 프롬프트에서 실험을 수행한 결과, sequence 길이가 짧고 batch size가 작을 때는 작은 draft 모델에 KV cache 압축이 효율적이다. 그러나 sequence와 batch size 둘 다 큰 경우에는 self-speculation이 더 좋은 성능을 보여준다. 이는 KV cache가 높은 batch size와 긴 sequence 조건에서는 병목을 일으키고 모델 파라미터 로딩이 미치는 영향이 상대적으로 작아지기 때문이다.

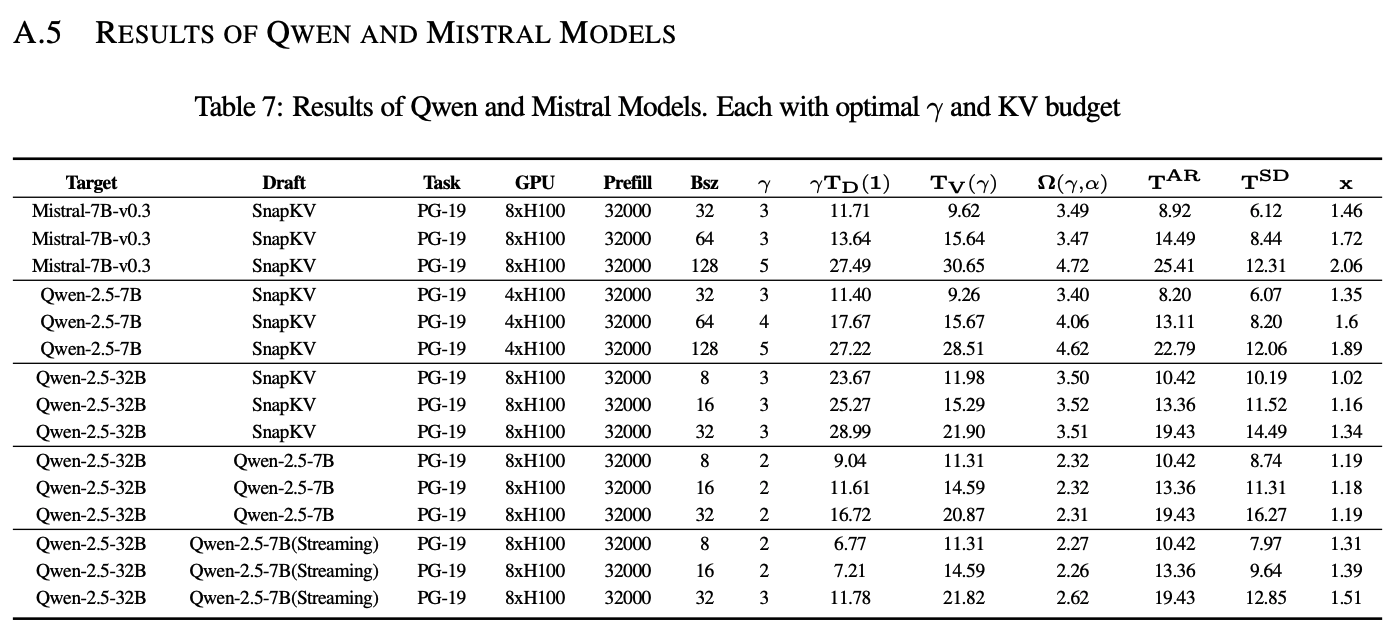
끝으로 부록에는 Qwen 2.5와 Mistral을 이용하여 모델마다 FLOPS와 Memory 비율과 acceptance rate 변화에 대한 실험 내용이 있었다. 데이터셋은 동일하게 PG-19를 사용하였는데, 전체적인 경향성은 LLaMA-3.1 8B 실험과 동일하게 나왔다고 한다.

결론 및 고찰

결론적으로 이전에 통념과는 다르게 speculative decoding이 높은 batch size와 긴 sequence에서도 KV cache 압축 기반의 draft 방식을 통해 먹힌다는 것을 증명한 내용이였다.

이직을 하면서 아마 내 주요 업무가 speculative decoding이 될 것 같다. 이전에 가장 근본이 되는 논문을 읽어서 speculative decoding에 대한 지식은 어느정도 있었지만, KV cache 압축 기법 같은 방식을 사용하면서 모르는 내용들이 좀 더 많았다. 특히 논문에서 압축을 적용 했을 때 acceptance rate가 증가하는 원인이 조금 이해가 되지 않는 면도 있었다. 이 부분을 조금 명쾌하게 알려줬으면 했는데, 이를 실험으로만 증명하고, 이에 관련된 수식 같은게 없어서 조금 아쉬운 논문이였다.

Hyunjoon Jeong

ML System 개발자 입니다.

이전 포스트

Qwen 3 Technical Report

다음 포스트