[ICML'24] MEDUSA: Simple LLM inference acceleration framework with multiple decoding heads

Hyunjoon Jeong·2025년 10월 19일

목록 보기

7/13

요즘 회사에서 Speculative decoding 관련 업무를 맡게 되면서 원래 자주 읽던 ML system 논문보다 fine-tuning 관련한 논문을 좀 더 많이 보게 되는 것 같다. 특히 speculative decoding의 경우, 조건에 따라 디코딩 단계에서 많은 latency를 줄일 수 있는데, 시스템적인 해결책만으로 풀 수 있는 문제는 아닌 것으로 보인다. 오늘 준비한 Medusa는 speculative decoding을 위해 추가적인 decoding layer를 도입해서 몇가지 결점을 해결한 논문이다.

https://dl.acm.org/doi/abs/10.5555/3692070.3692273

Speculative Decoding

Speculative decoding의 기본적인 원리에 대한 글은 아래에 작성한 이전 글을 통해 확인 할 수 있다.

https://velog.io/@with1015/ICML23-Fast-Inference-from-Transformers-via-Speculative-Decoding

Speculative decoding의 문제점 중 잘 알려진 것 중에 하나는, 적절한 draft 모델을 정하는 것이 어렵과 분산 시스템에서 활용하기 어렵다는 점이다. 이전 글에서 언급하였듯, draft 모델은 base가 되는 모델의 토큰 생성 분포를 어느정도 유사하게 따라 갈 수 있어야 acceptance rate가 잘 나오고, 이것이 speculative decoding의 속도와 직결 된다.

이러한 문제를 해결하기 위해서, Medusa는 decoding 단계에서 여러개의 decoding head를 붙여서 병렬로 후보 token을 동시에 검증 할 수 있도록 개선하고자 하였다.

Medusa

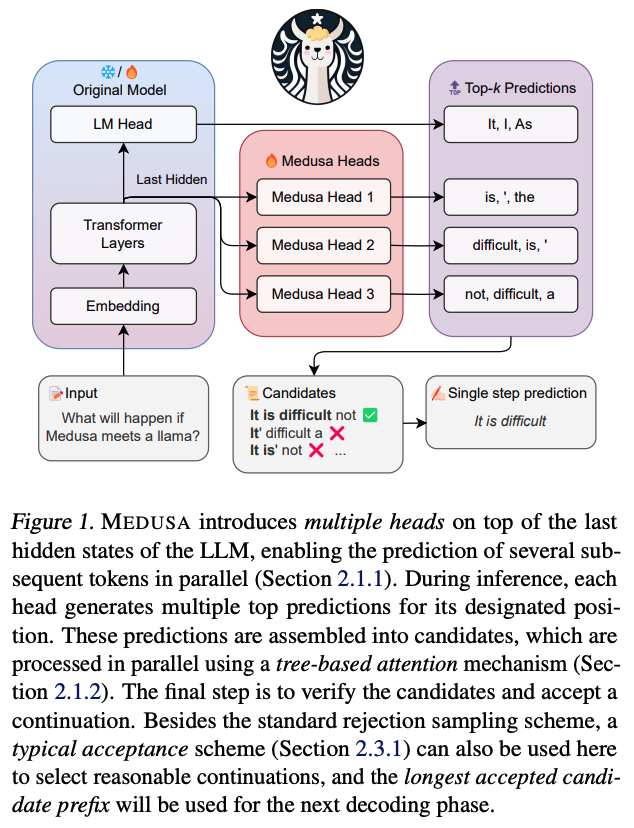
우선 Medusa는 이전의 speculative decoding처럼 [후보 토큰 생성 -> 후보 토큰 처리 -> 후보 토큰 수락] 3가지 단계로 decoding을 수행한다. Medusa에서는 우선 후보 토큰 생성을 위해서 Medusa head를 이용하고, 후보 토큰 처리를 위해 tree attention을 사용한다. 그리고 마지막 단계인 후보 토큰 수락 단계에서는 reject sampling이나 typical acceptance 방식을 이용한다.

Medusa heads

이전의 speculative decoding은 draft 모델 확보를 위해서 별도의 모델을 fine-tuing하는 방식을 사용 했는데, 그런 경우에는 학습을 위한 자원이 별도로 필요하다. GPU는 조상님이 내려주는게 아니기도 하거니와, 독립적으로 학습이 되는 경우, draft 모델이 생성한 결과의 acceptance rate가 떨어질 수 있다.

Medusa는 이러한 문제를 해결하기 위해, 원본이 되는 base 모델에 마지막 hidden state 위에 추가로 decoding head를 붙였다. 이를 Medusa head라고 한다. 원본 모델의 $t$ 시점에서 마지막 hidden state를 $h_t$ 라고 하고, 여기에 $K$ 개 만큼의 decoding head를 추가하면 각 head는 다음과 같이 토큰을 예측한다.

$k<K$ 번째 head는 $(t+k+1)$ 번째 토큰을 예측한다.
원본 모델의 head는 $(t+1)$ 번째 토큰을 예측한다.

Medusa head는 초기 파라미터를 원본 언어 모델의 head와 동일하게 맞추거나, 0으로 초기화 시킨다. 이렇게 하는 이유는, Medusa head가 초기 예측에서 원본 모델과 동일하게 일치 할 수 있도록 정렬 시키기 위해서라고 한다. 그리고 Medusa head의 구현은 residual connection을 가진 단일 FFN layer로 구성을 한다. activation function은 LLaMA 계열에서 사용 되는 SiLU를 사용한다.

Medusa head는 Medusa의 버전에 따라 다르게 학습이 된다. Medusa-1에서는 backbone이 되는 모델을 고정 시킨 상태에서 Medusa head만 학습 시킨다. 반면 Medusa-2에서는 joint training을 통해 backbone 모델과 동시에 학습 시킨다.

Tree attention

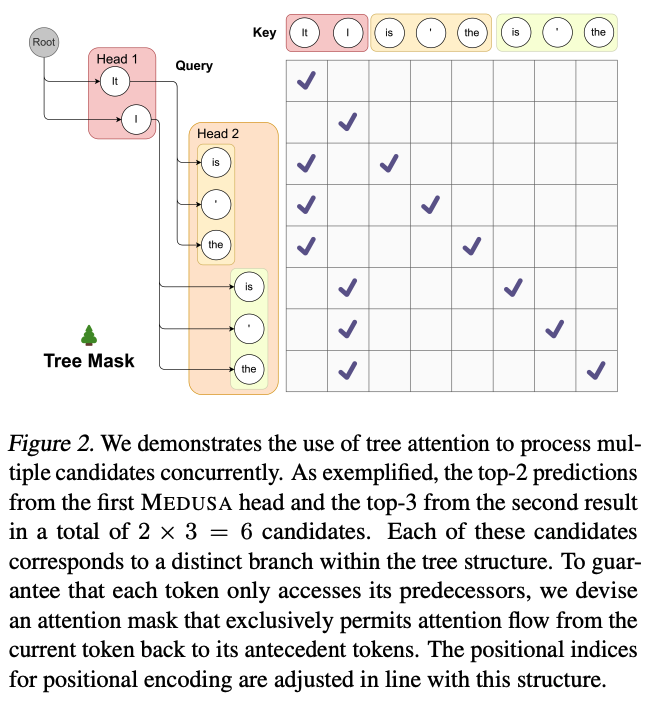
Medusa head를 이용하면 $K+1$ 개 만큼의 토큰에 대한 확률 분포를 얻게 된다. 이는 $K+1$ 길이의 후보 sequence가 된다. Medusa는 이러한 후보 sequence를 여러개 만들고, 동시에 활용하여 acceptance lenghth를 증가 시킨다. 보통 이런 후보가 많아지면 계산량도 증가하게 되는데, 이를 절감시키기 위해 tree attention을 사용한다.

tree attention은 이전의 causal attention과 다른데, 이는 같은 연속되는 sequence 내 토큰만 historical data로 사용 된다. Medusa는 top-down 방식으로, Medusa head에서 생성한 draft 구조를 기반으로 트리를 생성한다.

$k$ 번째 head에서는 상위 $s_k$ 개의 예측 결과를 사용하여 후보를 만들어낸다. ( $s_k$ 는 하이퍼파라미터이다.) 이 후보들은 상위 $k-1$ 에서 예측한 값들과 Cartesian product를 이용하여 구성이 된다. 위 그림을 예시로 설명하자면, $s_1=2, s_2=3$ 이 된다. 첫번째 head의 각 예측값들은 두번째 head의 예측값들과 결합이 될 수 있다. 그렇기 때문에 2레벨까지 내려 왔을 때, 생성 된 후보 토큰들의 개수는 $2\times 3=6$ 개가 생성이 된다.

새롭게 생성 되는 전체 토큰 수를 수식으로 만들면 다음과 같이 된다.

Generated\ Tokens = \displaystyle \sum_{k=1}^{K} \prod_{i=1}^k s_i

Medusa Training Strategy

앞서 잠깐 언급했듯이, Medusa는 2가지 학습 방법이 존재한다. 기본적으로는 모델을 고정 시킨 상태에서 Medusa head만 fine-tuning 할 수 있지만, backbone 모델과 함께 학습하는 경우가 정확도 향상에 더 좋았다고 한다.

Medusa-1 : Frozen backbone

backbone 모델이 고정이 된 경우, Medusa head의 예측과 정답 사이의 cross-entrophy loss를 이용한다. 예를 들어, 어떤 시점 $t+k+1$ 에서 정답 토큰인 $y_{t+k+1}$ 이 주어졌을 때, $k$ 번째 head의 loss값은 다음 수식처럼 정의 된다.

L_k = -\log{p_t^k(y_{t+k+1})}

$p_t^k(y)$ 는 $k$ 번째 head가 예측한 토큰 $y$ 의 확률이다. $k$ 가 커지면 $L_k$ 값이 더 커지는 경향이 있으며, 이는 $k$ 가 클수록 예측이 더 불확실하기 때문이다. 따라서 서로 다른 head 사이에서 발생하는 loss에 균형을 주기 위해서 $\lambda_k=0.8^k$ 값에 해당하는 가중치를 추가한다. 그렇게 되면 수식은 다음처럼 바뀐다.

L_{MEDUSA-1} = \displaystyle \sum_{k=1}^{K}-\lambda_k\log{p_t^k(y_{t+k+1})}

backbone 모델은 단순히 hidden state를 제공하는 역할만 하기 때문에 quantization과 같은 방식으로 메모리 사용량을 줄일 수 있다. 그리고 Medusa head만 학습하는 방식이기 때문에, A100 1대에서 Vicuna 7B 모델을 학습한다고 가정 했을 때, 60k ShareGPT 데이터셋 학습에서 5시간 밖에 걸리지 않았다고 한다.

Medusa-2 : Joint training

Medusa head의 정확도 향상을 위해서 backbone과 동시에 학습을 할 수 있는데, 이 경우 backbone 모델의 다음 토큰 예측 성능과 output의 퀄리티가 떨어질 수 있다. 그렇기 때문에 다음 3가지 방식을 추가하여 학습을 한다.

1. Combined loss

backbone 모델의 다음 토큰 예측 능력을 유지시키기 위해, Medusa의 loss에 backbone 모델의 cross-entrophy loss를 추가해주는 방식이다.

backbone model의 loss는 $k$ 값이 0일 때와 같기 때문에 다음과 같이 계산이 된다.

L_{LM}=-\log p_t^0(y_{t+1})

그리고, 이를 Medusa의 loss에 추가하면 아래와 같이 수식에 추가 할 수 있게 된다.

L_{MEDUSA-2}=L_{LM}+\lambda_0L_{MEDUSA-1}

2. Differential learning rate

backbone 모델은 이미 학습이 어느정도 된 상태이기 때문에 Medusa head만 더 빠르게 converge 할 수 있도록 서로 다른 learning rate를 적용하는 방식이다.

3. Head warm-up

학습 초기에 Medusa head의 loss가 너무 커서 큰 값의 gradient가 발생하는 경우가 있다. 이런 경우, backbone 모델의 파라미터를 왜곡시켜 정상적으로 학습이 불가능한 결과가 발생한다. 이를 방지하기 위해 다음과 같이 2단계의 학습 프로세스를 적용시켜야 한다.

1) backbone 모델을 고정한 후, Medusa head만 학습
2) backbone 모델과 Medusa head를 같이 학습 하되, backbone 모델의 $\lambda_0$ 값을 서서히 증가 시키는 warm-up 사용

Typical Acceptance

기존의 speculative decoding에서는 원본 모델의 분포와 일치하는 출력 토큰을 얻기 위해 reject sampling 방식을 사용한다. 예를 들어 draft 모델과 원본 모델이 완전히 동일하다고 가정 했을 때, greedy decoding을 사용하면 draft의 모든 출력이 항상 accept 되기 때문에 효율이 올라간다. 하지만 reject sampling은 draft 모델과 원본 모델을 독립적으로 sampling 하기 때문에 reject가 발생 할 수 있다.

또한 temperature 파라미터가 문제가 될 수 있는데, temperature가 높을 수록 원본 모델이 draft 모델의 출력 토큰을 accept 할 가능성이 높아진다. 그렇기 때문에 draft와 원본 모델이 정확하게 일치하지 않아도 acceptance rate를 향상 시킬 수 있다는 것을 발견했다.

Typical acceptance는 원본 모델이 생성할 가능성이 너무 낮지 않은 후보를 선택하는 전략을 사용한다. 이를 위해, 원본 모델의 예측 확률을 기준으로, 그 분포에 기반한 acceptance threshold를 정하게 된다.

예를 들어, 다음과 같은 context가 있다고 가정한다.

x_1, x_2, ... , x_n

이 때, Medusa head와 원본 모델의 head는 다음과 같은 후보 sequence를 만들 수 있다.

(x_{n+1}, x_{n+2}, ... , x_{n+K+1})

Typical acceptance는 각 토큰 $x_{n+k}$ 에 대해, 다음 조건이 만족 되었을 때, 해당 후보 토큰을 accept 하게 된다.

p_{original}(x_{n+k}|x_1, ... , x_{n+k-1}) > \min(\epsilon, \delta e^{-H(p_{original}(.|x_1, ... , x_{n+k-1}))})

여기서 각 파라미터는 다음을 의미한다.

$H(.)$ : 분포의 entropy 함수
$\epsilon$ : hard threshold
$\delta$ : entropy-dependent threshold

위 조건은 상대적으로 확률이 높은 토큰은 의미 있는 토큰일 가능성이 높다는 것과, 분포의 엔트로피가 높을 때는 여러 개의 합리적인 다음 토큰이 존재 할 수 있다는 아이디어를 변형한 결과라고 한다.

decoding 과정에서, 모든 token 후보는 위 조건으로 평가가 되고, 각 후보의 prefix 중 조건을 만족하는 가장 긴 부분을 accept하게 된다. 매 단계마다 최소 1개의 토큰은 생성이 되어야 하기 때문에, 첫 토큰은 greedy decoding으로 무조건 수락 되고, 그 이후 토큰에 대해서만 typical acceptance를 적용하게 된다.

LLM temperature 값에 따라 typical acceptance는 다음과 같은 결과가 발생한다.

temperature = 0이면, 가장 높은 확률의 토큰만 선택이 되기 때문에 greedy decoding과 동일하게 동작한다.
temperature > 0이면, greedy decoding 결과는 항상 조건을 만족하기 때문에 최대 속도 향상을 얻는다.
temperature가 증가 할수록 일반적으로 더 긴 sequence가 accept이 되는 경향이 있다.

내용이 조금 어려운데, 요약하자면 이렇다.

이전에 reject sampling은 매 토큰마다 확률비를 계산해야 하는 오버헤드가 있었고, acceptance rate가 낮기 때문에 속도가 느리다. 그래서 typical acceptance는 모델이 보기에 전체 확률 분포에서 확률이 너무 높거나 낮은 토큰은 outlier로써 버리고, 그 중간에 속하는 토큰만 취하는 전략이다.

Self-Distillation

일반적으로 Huggingface에 유명한 모델들을 보면, 모델만 공개하고 학습 데이터를 공개하지 않았거나, 모델이 RLHF를 통해 사람의 피드백을 거쳐 기존의 학습 데이터와 출력 분포가 다른 경우가 많다. 이를 위해서 Medusa는 모델이 자신이 직접 Medusa head를 위한 학습 데이터를 생성하게 하고, 이를 모델의 실제 출력 분포와 일치 시키는 방식을 제공하고 있다.

데이터셋 생성

우선 seed가 될 데이터셋 하나를 골라야 한다. 이는 타겟이 되는 모델과 유사한 도메인이여야 한다. 예를 들어 chat model의 경우, ShareGPT를 사용해야 한다. 데이터셋이 정해졌다면, 다음 방식을 사용하여 생성한다.

seed dataset의 프롬프트를 추출하여 모델에게 응답을 생성하도록 한다.
multi-turn 샘플이 필요한 경우, seed dataset의 프롬프트를 순차적으로 입력하여 대화 내용을 얻는다.
만약 대화의 양쪽 역할을 모두 학습한 모델인 경우, 모델을 self-talk 시키는 방식으로 대화 내용을 얻는다.

Medusa-1 학습

Medusa-1의 경우, 위와 같이 생성 된 데이터셋을 사용해도 Medusa head 학습에 충분하다.

Medusa-2 학습

하지만 Medusa-2는 경우가 좀 다른데, 단순하게 위와 같이 생성 된 데이터셋을 사용하면 반대로 생성되는 출력의 품질이 떨어지는 현상이 발견된다. 이는 backbone 모델만 학습을 해도 동일한 현상이 발생하는데, 이를 통해 저자들은 backbone 모델을 학습 할 때, 정답 토큰이 아니라 원본 모델의 확률 예측을 라벨로 사용해야 한다는 점을 유도해냈다.

이 방식은 기존에 knowledge distillation과 유사한데, 구체적인 수식은 다음과 같다.

L_{LM-distill} = KL(p_{original, t}^{0} || p_t^0)

여기서 $p_{original, t}^{0}$ 는 원본 모델의 t번째 위치에서의 확률 분포이고, $p_t^0$ 는 학습중인 모델의 예측 확률 분포이다. 이를 KL divergence를 이용하여 원본 모델의 출력을 학습 모델이 모방하도록 유도한다.

추가로, knowledge distillation은 teacher와 student 모델 2개를 유지해야 하기 때문에 메모리 사용량이 높다. Medusa는 LoRA처럼 paramter-efficient adapter를 이용하여 fine-tuning을 한다. 원본 모델은 adapter가 꺼진 상태의 모델이고, 학습 모델은 adapter가 켜진 상태의 모델이 된다. 이 방식으로 학습 시 두 모델을 동시에 로드 할 필요가 없기 때문에 메모리의 추가 사용 없이 distillation이 가능하다.

주의해야 할 사항은, self-distillation을 사용 할 때, quantization이 되지 않은 LoRA를 사용해야 한다. 그렇지 않으면 teacher에 해당하는 모델이 quantization 된 형태가 되기 때문에 생성되는 품질이 낮아질 수 있다.

Optimized Tree Construction

이전에 tree attention을 구성하는 방법으로 Cartesian product를 사용했었다. 하지만 tree 구조도 무한정 팽창 할 수 없기 때문에, 전체 노드 수가 어떤 budget을 가지고 있다면 항상 최적인 방식은 아니다.

각 Medusa head가 만드는 top 예측값들로 구성되는 토큰 후보는 accuracy가 서로 다를 수 있다. 그래서 accuracy 추정치를 활용하여 tree를 더 효율적으로 구성 할 수 있다. calibration 데이터셋을 사용하면 각 head의 상위 예측값에 대한 정확도 계산을 근사 할 수 있다.

$a_k^i$ 를 $k$ 번째 head의 $i$ 번째 상위 예측값의 정확도라고 가정한다. 이러한 정확도들이 서로 독립적이라고 가정하면, 다른 head들의 상위 예측값인 $[i_1, i_2, ... , i_k]$ 로 구성 된 후보 sequence의 전체 정확도는 다음과 같이 근사 할 수 있다.

\prod_{j=1}^{k}a_j^{i_j}

이는 바꿔 말하면 각 head의 예측 정확도들을 곱하면 후보 sequece들의 전체 신뢰도를 추정 할 수 있다는 말이 된다. 그래서 후보 sequence의 expected acceptance length는 다음과 같이 계산이 된다.

\sum_{[i_1, i_2, ... , i_k] \in I} \prod_{j=1}^{k}a_j^{i_j}

정리하자면, tree에 노드를 하나씩 추가하면서 tree attention을 구축한다고 가정해보자. 이 때, 새로 추가되는 노드가 기대값에 기여하는 정도가 그 노드의 정확도에 해당된다. 따라서 greedy 알고리즘을 이용하여 최적 tree를 다음과 같이 구성 할 수 있다.

현재 tree에서 연결 될 수 있는 노드 중에 가장 높은 정확도를 가진 노드를 선택해서 추가한다.
tree의 전체 노드 수가 원하는 budget에 도달 할 때까지 이를 반복한다.

실험 결과

실험에서 Medusa-1과 Medusa-2의 평가를 위해 Vicuna 및 Zephyr 모델을 사용하였다. Vicuna는 LLaMA를 베이스로 만든 모델인데, 33B의 경우 fine-tuning 데이터셋에 접근 할 수 없는 모델이다. Zephyr 모델은 RLHF 방식을 거친 모델로, self-distillation 평가에 적합하다.

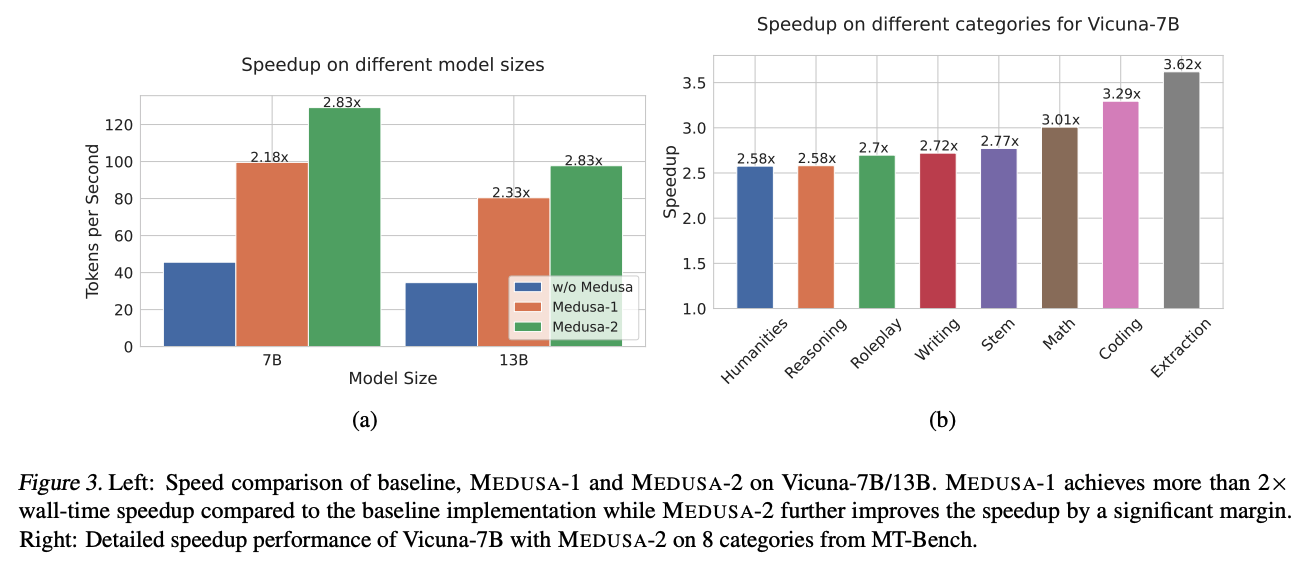
위 그래프는 Vicuna 모델에서 베이스라인을 huggingface를 사용하여 Medusa의 토큰 처리 속도 향상을 나타낸 그래프이다. Medusa-2는 다양한 카테고리에서도 속도 향상이 이루어졌다.

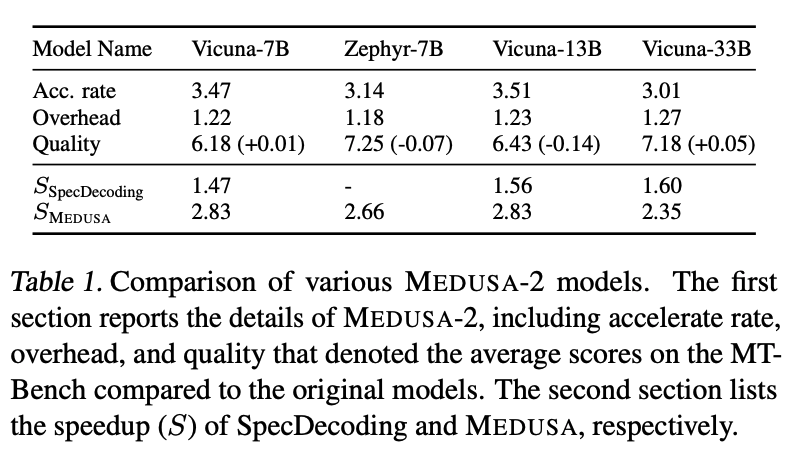
위 표는 self-distillation을 사용 했을 때, Medusa-2 모델의 속도 향상 비율, 추론 시 발생하는 오버헤드, 그리고 MT-bench 평가 점수를 비교한 결과이다. 모든 모델에서 Medusa의 속도는 향상이 되었고, Vicuna 33B의 경우 출력 품질 또한 원본 모델과 거의 동일하게 유지가 되었다.

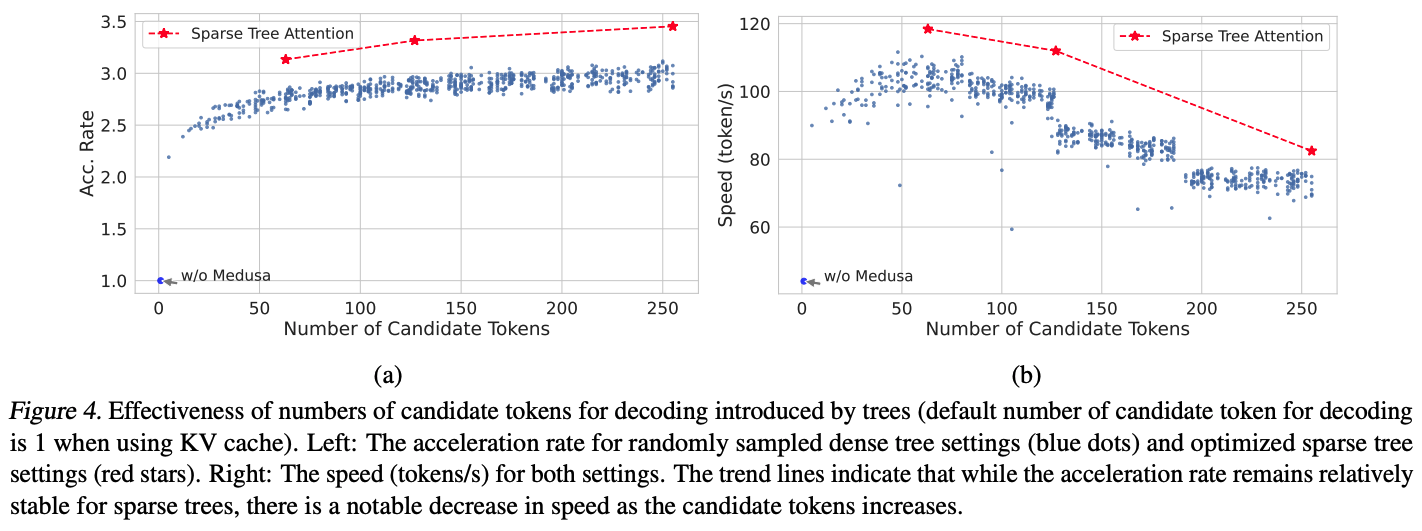
위 그래프는 tree attention에 대한 실험이다. 빨간 선은 최적화 된 sparse tree 구성이고, 파란 선은 무작위로 샘플링 된 dense tree 구성을 의미한다. (a) 그래프에서 sparse tree는 노드 수가 64개 밖에 되지 않음에도 256개의 노드를 가지는 dense tree보다 더 높은 성능 향상을 보여준다. (b) 그래프에서는 실제 토큰 생성 속도가 감소하는데, 이는 tree가 복잡해지면서 발생하는 계산량 증가로 인한 오버헤드가 원인이 된다.

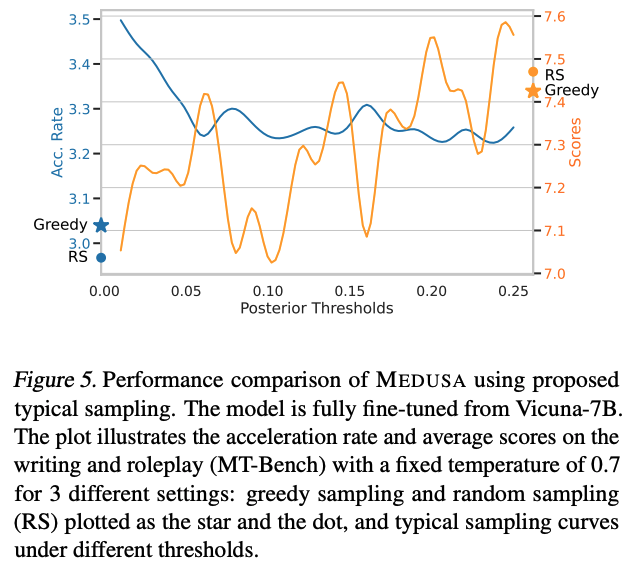
위 그래프는 typical acceptance의 threshold 값에 따른 모델 성능 비교를 보여준다. $\epsilon$ 값을 0.01에서 시작하여, 0.25까지 0.01 단위로 증가시켰을 때, 다음과 같은 trade-off를 발견했다고 한다.

$\epsilon$ 값이 커질수록 생성 되는 품질은 향상 되지만 속도 향상률은 떨어진다.
temperature 값을 높게 사용 하는 경우, 랜덤 샘플링이 greedy보다 더 좋은 성능을 보여준다.
typical sampling은 $\epsilon$ 값이 커질수록 랜덤 샘플링과 유사한 수준의 성능을 보여준다.

마지막으로 위 표는 Vicuna 7B 모델에서 서로 다른 fine-tuning 방식에 대한 성능 차이를 보여준다. Medusa-1처럼 head만 fine-tuning 하는 경우, 생성 품질 저하 없이 2.18배 속도 향상을 보여준다. Medusa-2의 경우, 동일 품질을 유지하면서 2.83배까지 속도 향상이 이루어졌다. 하지만 Medusa head와 모델을 직접 한 번에 fine-tuning 하는 경우, 오히려 생성 품질은 저하 되었다. 이를 통해 head warm-up을 통해 2단계를 거친 fine-tuning이 필요하다는 것을 입증하였다.

결론 및 고찰

Medusa는 결론적으로 단순한 head 역할의 레이어를 추가하여 fine-tuning 하는 방식으로 speculative decoding이 가지는 draft 모델 확보의 어려움을 해결하려고 했다. 또한 이를 통해 순차적으로 decoding을 하는 방식 대신 여러개의 토큰을 병렬로 생성 할 수 있도록 구성하였다.

이 논문을 읽으면서, 비교적 단순한 방식으로 speculative decoding을 개선하려고 시도한 것은 알겠지만, 아무래도 학습이 가미 된 방식이다보니 내가 직접 사용하고 이해하기에는 어려운 방식이였다. (역시 ML 시스템은 학습 없이 가야한다고 생각한다.) 또한 논문이 붙은 시점은 24년도 ICML이지만, arXiv에는 오래 전부터 있었던 논문이다보니 vLLM과 비교한 지표가 없어서 아쉬운 면도 있었다.

Hyunjoon Jeong

ML System 개발자 입니다.

이전 포스트

[ICLR'25] MagicDec: Breaking the Latency-Throughput Tradeoff for Long Context Generation with Speculative Decoding

다음 포스트