[NeurlPS'25] MoESD: Unveil Speculative Decoding's Potential for Accelerating Sparse MoE

Hyunjoon Jeong·2025년 10월 24일

목록 보기

9/13

사내에서 speculative decoding을 연구하면서, 문득 생각보다 MoE를 타겟으로 하는 논문을 본적이 없는 것 같았다. 그나마 최근에 봤던 Eagle 논문에서 Mixtral을 이용했었는데, 성능 자체는 1.5배 더 좋아졌다고 하지만 expert의 활성화 문제로 인해서 이는 dense-only LLM에 비해 낮은 성능 이득을 본 것이라고 적혀 있었다. 그래서 최근 논문 중에 MoE를 타겟으로 하는 NeurlPS 논문 하나를 찾게 되었다.

https://neurips.cc/virtual/2025/poster/119061

MoE와 Speculative Decoding

이전에 MoE 연구에서 speculative decoding을 사용하지 않았던 이유 중 하나로, MoE 모델을 이용하여 draft 모델이 생성한 토큰을 검증 할 때, expert가 과하게 활성화 되는 문제가 있었다. 이전에 Eagle에서 Mixtral 8x7B를 이용하여 실험을 했을 때, 이와 같은 문제가 있었다. 또한 Cascade라는 논문에서 동일한 문제가 발견이 되기도 했고, 어떤 경우에는 1.5배 느려지는 문제도 발생했었다.

Roofline Model

MoE에서의 speculative decoding에 대해 설명하기 전, 논문에서는 LLM 워크로드를 사용 할 때 발생하는 latency는 어떻게 결정되는가에 대해 설명한다. GPU에서 LLM에 사용 되는 CUDA 커널들을 실행 할 때, GPU 연산과 파라미터 값들의 메모리 이동이 파이프라인화가 되어 적절히 overlap 시키는 방향으로 실행이 된다. 이 때, 연산이 더 오래 걸리느냐, 아니면 메모리 이동이 더 오래 걸리느냐에 따라 병목이 발생하는 지점이 달라지면서 전체 처리 시간을 결정하게 된다.

이에 따라 roofline model로 두 요소들 사이의 관계를 정의 할 수 있다. 우선 하드웨어가 가지는 ridge point를 RP라고 부르고, 소프트웨어가 가지는 arithmetic intensity를 AI라고 부르기로 한다. 그래서 두 요소를 수식으로 정리하면 다음과 같이 정의가 된다.

RP = \frac{Peak\ computation\ power\ (FLOPs)}{Peak\ memory\ bandwidth\ (bytes/sec)}

AI = \frac{Computation\ operation\ (times)}{Memory\ access\ volume\ (bytes)}

이를 통해 RP값과 AI값의 상관 관계를 만들 수 있고, 상관 관계에 따라 LLM 워크로드가 computation-bound인지, 아니면 memory-bound인지를 결정 할 수 있게 된다.

AI < RP : memory-bound 상태로, 계산량을 늘려도 전체 처리 시간이 증가하지 않는다.
AI > RP : compute-bound 상태로, 계산량이 늘어나면 처리 시간이 늘어난다.

Target Efficiency

MoESD 논문에서는 워크로드가 가지는 부하나 모델 구조와 같은 시스템적인 요인이 speculative decoding에 얼마나 영향을 미치는지를 정의한 요소를 target efficiency라는 이름으로 사용한다. 이를 정의하기 위해, 먼저 speculative decoding의 처리 시간을 수식화 하면 다음과 같다.

우선 speculative decoding은 다음 3가지 단계를 거쳐서 이루어지는데, 이를 $R$ 번 반복하여 길이 $S$ 만큼의 sequence를 뽑아낸다.

draft 모델이 speculation 전략에 따라 $\gamma$ 개의 토큰을 제시한다.
target 모델이 생성 된 토큰을 검증한다.
rejection sampling을 통해 draft 모델과 target 모델의 logit을 비교하여 잘못 예측 된 토큰을 폐기한다.

batch size $b$ , 토큰 수 $s$ 만큼을 각각 draft 모델과 target 모델에서 forward pass를 할 때 발생하는 시간을 $T_D(b, s)$ $T_T(b,s)$ 라고 표현한다면, speculative decoding을 사용하여 $B$ batch size 만큼 요청을 처리 할 때 발생하는 전체 시간은 다음과 같이 작성한다.

T_{SD} = R \times (T_{propose} + T_{verify} + T_{reject}) = R \times [\gamma T_D(B, 1) + T_T(B, \gamma)+T_{reject}]

위 수식을 조금 해석해보자면, 위에 언급 된 대로 speculative decoding은 draft 모델이 토큰을 일정량만큼 제안하는 propose 단계, 검증하는 verify 단계, 그리고 잘못 예측 된 토큰을 제거하는 reject 단계를 $R$ 번 거친다. propose 단계는 토큰을 1개씩 $\gamma$ 번 draft 모델을 통과해야 한다. 그리고 target 모델은 draft에서 생성 된 $\gamma$ 개의 토큰을 검증해야 한다.

Speculative decoding의 수식을 일반적인 auto-regressive의 디코딩 시간인 $T_{AR}$ 에 대응시키면 속도 향상 비율을 얻어 낼 수 있다.

Speedup = \frac{T_{AR}}{T_{SD}} = \frac{S \times T_T(B, 1)}{R \times [\gamma T_D(B, 1) + T_T(B, \gamma)+T_{reject}]}

auto-regressive의 경우에는 $S$ seqeunce 길이만큼 토큰을 1개씩 target 모델에서 만들기 때문에 $S$ 값과 $T_T(B, 1)$ 의 곱으로 나타낼 수 있다. 위 수식을 한 번 더 다음과 같이 정리 할 수 있다.

Speedup = \frac{S}{R} \times \frac{1}{\gamma\times\frac{T_D(B,1)}{T_T(B,1)}+\frac{T_T(B,\gamma)}{T_T(B,1)}+\frac{T_{reject}}{T_T(B,1)}}

이렇게 정리 할 경우, 분모가 3개의 항으로 바뀌게 된다. 각 항의 특징은 다음과 같이 분석이 된다.

$\frac{T_D(B,1)}{T_T(B,1)}$ : draft 모델과 target 모델의 forward 시간 비율로, 두 모델의 상대적인 크기를 반영한다. 일반적으로 0.1 이하 값으로 유지가 되어야 효율적인 speculation decoding을 할 수 있다.
$\frac{T_T(B,\gamma)}{T_T(B,1)}$ : 여러 토큰을 한 번에 처리하는 target 모델의 forward 시간 비율이다. 세 항 중에 가장 값이 큰 항으로, 실질적으로 이 항이 전체 속도 향상에 큰 영향을 준다.
$\frac{T_{reject}}{T_T(B,1)}$ : reject sampling 시간 비율로, 모델의 추론 시간이 아니라 단순 샘플링 연산이다. acceptance rate가 작을 수록 이 값이 매우 작아진다.

MoESD에서 정의하려는 target efficiency는 이 중 2번째 항의 역수로 정의한다.

Target\ Efficiency = \frac{T_T(B,1)}{T_T(B,\gamma)}

이 값이 2번째 항의 역수이기 때문에, target efficiency가 커진다는 것은 속도 향상 비율이 증가하여 실질적으로 speculative decoding이 효과를 보게 된다는 것을 의미한다. 이를 통해 MoESD에서는 acceptance rate를 증가시킬 수 있는 알고리즘적인 최적화와 모델 구조, 워크로드의 특성을 나타내는 시스템적인 최적화를 분리하여 분석을 한다.

Target efficiency의 값이 작아지는 주된 원인은 2가지다.

Compute-bound로 전환 : batch size $B$ 가 작아지면 시스템은 memory-bound 상태가 된다. 그렇기 때문에 target efficiency가 1에 수렴하게 된다.
추가 메모리 로드 : 작은 batch size에서는 더 많은 expert가 활성화 되어 로드되어야 한다. 그렇기 때문에 시스템은 memory-bound 상태로 남게 된다.

Toekn generation ratio

위 수식에서 한가지 더 특이한 항이 있다. 가장 앞에 붙는 sequeunce 길이 $S$ 값을 $R$ round 값으로 나누는 항이 있는데, 저 항은 speculative decoding의 한 번의 라운드가 평균적으로 얼마나 많은 토큰을 실제로 생성할 수 있는가를 의미한다. 이 값을 다음과 같은 다른 수식으로 바꿀 수 있다.

\frac{S}{R} = \sigma \times (\gamma + 1)

$\gamma$ 값은 speculative decoding을 할 때 draft 모델이 한 번에 생성하는 후보 토큰의 수인데, 이 값을 $\sigma$ 값과 결합하여 라운드 당 발생 토큰 수를 계산 할 수 있다. 이 때, $\sigma$ 를 draft 모델이 제안한 토큰이 모두 accept 되었을 때를 가정한 최대 생성량 대비 실제 생성 된 비율을 의미한다. 이 값은 다음과 같이 정의가 된다.

\sigma = \frac{expected\ generated\ tokens}{maximal\ possible\ accpted\ tokens} = \frac{\frac{1-\alpha^{\gamma+1}}{1-\alpha}}{\gamma + 1}

위 식에서 $\alpha$ 는 acceptance rate로, speculative decoding에서 일반적으로 사용 되는 target 모델이 draft 모델의 새로운 토큰을 받아들일 확률을 의미한다. 참고로 speculative decoding은 target 모델이 검증을 하는 과정에서 자연스럽게 다음에 나올 토큰 확률도 계산을 하게 된다. 이는 target 모델 또한 LLM이기 때문에 발생하는 자연스러운 과정인데, 그렇기 때문에 최대 accept 된 토큰 수에 관련 된 항에 1이 추가 되는 이유이다.

Batch size와 MoE Speculative Decoding

일반적으로 speculative decoding은 작은 batch size를 가질 때 유효하다. 비록 이 가정 자체는 MagicDec에서 어느정도 무너진 가정이긴 하지만, MoE 모델로 봤을 때는 작은 batch size를 사용하더라도 speculative decoding이 비효율적으로 작용한다. MoESD는 중간 정도의 batch size 구간에서 MoE를 target 모델로 사용했을 때, speculative decoding 사용이 가능함을 보인다. 특히 MoE의 sparsity가 높을수록 그 이점이 커지는 것을 보여준다.

우선 다음과 같이 MoE 모델에서 expert가 활성화 되는 수의 기댓값을 계산 할 수 있다. 베르누이 확률변수 $X_i$ 를 expert $i$ 가 활성화 됐을 때를 1, 비활성화 됐을 때를 0 값으로 잡고, 각각의 expert들이 independet identical distribution (i.i.d)라고 가정한다. 그러면 활성화 되는 expert의 기대 수인 $N$ 을 다음과 같이 나타낼 수 있다.

N = \sum_i E[X_i] = \sum_i P(X_i) = E \cdot P(X)

가장 오른쪽에 정리 된 항을 통해 정리하게 되면, $E$ 는 전체 expert의 수, 그리고 $P(X)$ 는 임의의 expert가 활성화 될 확률이고, 그 둘의 곱으로 나타낼 수 있다. 전체 expert 수는 쉽게 알 수 있는 반면, $P(X)$ 값은 추가적인 수식을 계산해야 한다. $t$ 개의 토큰이 MoE의 라우터 게이트를 통과 할 때, $K$ 를 토큰 당 활성화 되는 expert의 수라고 하면, 다음과 같이 표현이 된다.

P(X) = 1 - P(None\ of\ the\ t\ tokens\ activates\ the\ expert) = 1 - \bigg(\frac{E-K}{E}\bigg)^t

전체 확률에서 expert가 어떤 토큰에도 선택 되지 않을 확률을 계산해서 빼는 수식으로, 이는 전체 expert 수에서 토큰 당 활성화 되는 expert의 수를 이용하여 구할 수 있다. 그리고 이를 $t$ 개의 토큰이 수행하기 때문에 $t$ 값 만큼 확률을 중첩하여 거듭제곱을 시켜준다.

위 식을 정리해서 $t$ 개의 토큰이 들어올 때, 활성화가 되는 expert의 수의 기대값을 다음과 같이 정의 할 수 있다.

N(t) = E\cdot\bigg[1-\bigg(\frac{E-K}{E}\bigg)^t \bigg]

위 식은 모든 expert들의 load balancing이 균등하게 이루어질 때를 가정한다. 그렇기 때문에 MoE의 학습이 잘 이루어졌다는 가정을 해야 한다. 어차피 load balancing이 무너지면 expert parallelism의 효율이 떨어지기 때문에, 정상적인 상황이라면 위 식이 잘 먹히게 된다.

Expert가 거의 모두 활성화 되는 토큰 수

MoESD에서 제일 중요한 부분을 선택하라면 이 부분을 알아야 할 것이다. 위 수식을 따르면, $t$ 값이 커지만 대괄호 내부 항이 1에 수렴하기 때문에 활성화 되는 expert의 수는 전체 expert 수에 가까워지게 된다. 실제 워크로드에서는 $N(t)$ 는 discrete한 유한값이기 때문에 MoESD는 전체 expert 중에서 95% 이상 활성화가 되면 거의 모두 활성화가 되었다고 정의 ( $\tau = 0.95$ ) 한다.

만약 MoE가 sparsity를 가져서, $K=\rho E$ ( $\rho$ 는 sparsity값)으로 정의하면, 모든 expert가 활성화 되기 위한 토큰 수의 threshold를 다음과 같이 구할 수 있다.

N(t_{threshold}) = E \cdot [1-(1-\rho)^{t_{threshold}}] \geq \tau \cdot E

이를 $t_{threshold}$ 를 표현하도록 정리하면 다음과 같이 된다.

t_{threshold} = \lceil \log_{1-\rho}(1-\tau) \rceil

batch size $B$ 가 $t_{threshold}$ 를 넘게 되면 expert 활성화가 포화 상태에 도달하게 된다. 그 경우, MoE는 더 많은 expert 로드를 위해 추가적인 메모리를 요구하게 된다. 그러면서 시스템이 memory-bound로 남게 된다. 만약 batch size를 지속적으로 증가 시키는 경우, 시스템은 compute-bound로 전환이 되면서 speculative decoding으로 인한 MoE 가속이 불가능해진다.

MoE의 sparsity는 compute-bound 전환을 지연시킨다.

$t$ 개의 토큰이 MoE에 들어왔을 때, 활성화 되는 expert의 수를 $N(t)$ 로 정의하였다. 각 토큰은 $K$ 개 만큼의 expert를 활성화 하고, 이에 따라 각 expert가 평균적으로 처리해야 하는 토큰 수 $t_{exp}$ 는 다음과 같다.

t_{exp}(t,\ \rho) = \frac{t\cdot K}{N} = \frac{t\cdot (\rho E)}{E\cdot (1-(1-\rho)^t)} = \frac{\rho t}{1-(1-\rho)^t}

위 식에서 MoE의 sparsity를 나타내는 $\rho$ 값이 작아질수록 expert 하나가 처리해야 하는 토큰의 수는 감소하게 된다. 그렇기 때문에 각 parameter 로드 당 throuhgput이 감소하게 되면서 시스템은 memory-bound 방향으로 움직이게 된다.

그 결과, GPU의 arithmetic unit의 활용률이 낮아지게 되면서 speculative decoding의 검증 단계는 여분의 연산 자원을 활용하여 추가 latency 없이 병렬 검증이 가능해진다. 만약 $\rho=1$ 인 경우는 dense 모델이 되는 경우로, FFN이 최대 arithmetic intensity를 찍게 되는 경우다. 이렇게 되는 경우, 토큰 수가 증가할수록 시스템은 빠르게 compute-bound로 전환이 된다.

MoESD에서 한 가지 중요한 가정이 있는데, 위에 적힌 모든 수식이 먹히는건 MoE의 FFN이 모델 전체에서 차지하는 비중이 충분히 큰 경우이다. 만약 attention이 극단적으로 큰 경우, MoE의 sparsity는 시스템의 성능에 영향을 주지 못하게 된다.

Speculative Decoding의 속도 향상을 위한 모델링

앞에 내용을 정리하자면, speculative decoding을 이용하여 모델을 가속 시킬 때의 핵심은 모델의 forward pass에 걸리는 시간을 수식화하여 분석하는 것이다. 이에 따라 MoE 모델에서 forward pass를 할 때 실행 시간에 미치는 주요 원인은 3가지로 정리 할 수 있다.

Roofline 모델 효과
활성화 되는 expert의 수
각 expert마다 처리해야 하는 작업량

여기에 추가로 MoESD에서는 GPU의 실행은 동적이기 때문에 몇가지 보정을 위한 파라미터를 추가하였다. 추가 파라미터들은 GPU에서 측정 된 결과에 따라 자동으로 보정이 된다고 한다.

Roofline 모델 효과

Roofline 모델의 효과는 입력으로 들어가는 토큰 개수 $t$ 값에 따라 실행 시간이 증가하는 현상으로 나타난다. 증가율은 초기에는 완만하면서 가속이 되다가 안정화가 된다.

토큰 수가 작을 때

토큰의 수가 작으면 모델 파라미터를 GPU SM 코어에 로드하는 시간, 즉 메모리 접근이 연산 시간보다 길어진다. 그렇기 때문에 memory-bound 현상이 일어난다. 결과적으로 파라미터의 크기가 주어지면 메모리 접근 시간은 일정하게 유지 된다.

토큰 수가 커지는 경우

토큰 수 $t$ 값이 커지면 연산 시간이 모델 파라미터 로드 시간을 초과하게 된다. GPU의 arithmetic unit은 고정이 되어 있기 때문에 연산량에 linear하게 비례하게 된다. 즉, memory-bound에서 compute-bound로 전환 된다.

이러한 경향을 수식으로 나타내면 다음과 같다.

G(t;\ \lambda RP,\ s) = \begin{cases} s\cdot t,\ t \leq \lambda RP \\ s\cdot \lambda RP[1+\ln(s)\cdot (t-\lambda RP)],\ t>\lambda RP \end{cases}

여기서 $\lambda RP$ 는 memory-bound와 compute-bound의 전환 지점을 나타내고, $s$ 는 실행 시간의 증가율을 나타낸다. $RP$ 는 앞서 언급한 하드웨어의 ridge point를 의미한다. $\lambda$ 는 1보다 작은 상수 값으로, 실제 GPU 메모리가 가지는 bandwidth의 활용 효율의 한계를 반영한다.

활성화 되는 expert의 수

활성화 되는 expert의 수가 많아지면 메모리 접근량이 증가하여 처리 시간이 늘어난다. 이는 앞서 정리한 $N(t)$ 수식으로 표현 할 수 있으며, 이는 모델 구조와 워크로드가 활성화 되는 expert 수에 영향을 미친다는 것을 알 수 있다.

각 expert마다 처리해야 하는 작업량

MoE가 라우터를 거치고 나면 각 expert는 처리해야 하는 토큰을 전체 토큰으로부터 할당 받게 된다. 이에 따라 각 expert는 전체 토큰 $t$ 가 아니라 일부 토큰인 $t_{exp}(t, \rho)$ 를 처리해야 한다. 그렇기 때문에 MoE 모델의 roofline은 $G(t)$ 대신 $G(t_{exp})$ 를 사용해야 하고, 이는 MoE의 희소성에 영향을 받게 된다. 즉, MoE의 희소성이 높아지면 입력 토큰 수가 늘어날 때, memory-bound에서 compute-bound로의 전환이 늦어진다.

전체 모델 표현 및 파라미터 보정

MoE의 경우 위 3가지 사항이 모두 작용한다. 이를 결합시킨 후, 4개의 추가 파라미터를 이용한다. 각 파라미터에 대한 설명은 다음과 같다.

$bias$ : 고정된 파라미터를 로드하는데 걸리는 시간
$k_1 \cdot G(t)$ : 토큰 수 증가에 따른 실행 시간 증가
$k_2 \cdot N$ : N개의 활성화 된 epxert를 로드하는데 필요한 시간
$k_3 \cdot G(T_{exp})$ : 각 expert 마다 워크로드 증가에 따른 실행 시간 증가

위 최적화 파라미터와 함게 위와 같은 알고리즘으로 speculative decoding으로 인한 속도 향상의 전체 모델링을 얻을 수 있다.

Theoretical Findings

위의 이론적인 분석을 통해 speculative decoding이 MoE에 적용이 되었을 때, 중간 규모의 batch size에서 효과가 있음을 발견해냈다. MoESD의 저자들은 이러한 크기의 batch size가 대규모의 트래픽이 들어오는 환경보다는 개인형 서비스에서 유리하다고 주장한다. 특히 SLO 제약을 받는 LLM 서비스인 경우, batch size가 지나치게 커지면 오히려 latency 제약에 걸리기 때문에 중간 크기의 batch size가 더 많이 사용됨을 어필했다. 마지막으로 speculative decoding이 적용 된 MoE가 기존의 latency와 throuhgput 사이의 trade-off를 완화 시키는 것을 발견해냈다. 즉, batch size가 증가함에 따라 latency와 throughput이 동시에 개선되는 구간이 존재함을 발견했다. 정리하자면, 중간 규모의 batch size에서 speculatvie decoding이 적용 된 MoE는 다음과 같은 현상이 발생한다.

모든 모델 파라미터가 메모리에 로드 되어야 한다. 즉, 작은 batch size처럼 선택적으로 동작하지 않는다.
하지만 GPU 연산 자원은 큰 batch size일 때와 달리 충분히 활용 되지 않는 상태이다.

Expert offloading

MoE 모델이 GPU 메모리를 초과하는 경우, FFN 파라미터를 CPU에 오프로딩 하는 경우가 존재 할 수 있다. 이 때, 모델 파라미터를 로드하는 bandwidth는 PCIe 수준까지 떨어지게 된다. 따라서 memory-bound 상태가 되면서 speculative decoding에 유리한 환경이 발생한다. 이 경우, 추가적인 계산이 처리 시간을 증가시키지 않게 된다. 다만 expert를 prefetching 하거나, caching하는 방식의 기법은 중간 크기의 batch size에서 거의 모든 expert가 활성화가 되기 때문에 효율이 떨어진다.

Expert parallelism

expert가 여러 GPU에 분산 되어 배포 되는 경우에는 활성화 되는 expert의 수나, expert 당 처리 토큰 수에 영향을 주지 않기 때문에 이전 분석 결과 그대로 적용이 가능하다. 또한 MoE 구조에서 FFN 외의 요소들도 병렬화가 되기 때문에 expert의 FFN이 전체 처리 시간에 대부분을 그대로 차지하게 된다. 거기에 expert parallism에서 발생하는 네트워크 I/O bound를 감안하면 expert parallelism을 적용하더라도 memory-bound 상태라는 것을 알 수 있다. 오히려 작은 batch size에서 speculative decoding이 가지는 비효율성이 사라질 수도 있는데, 이는 다수의 GPU가 추가 memory bandwidth를 줄 수도 있기 때문이다.

실험 결과

실험을 위해서 MoESD는 Qwen2와 Mixtral을 사용했다. Mixtral의 경우, Eagle 논문의 방식으로 학습 된 speculation head를 사용하였다. 반면 Qwen2는 57B-A14B-instrcut 모델을 target 모델로 사용하고, 0.5B-instruct 모델을 draft로 사용하였다. 그리고 expert sparsity에 따른 변화를 실험하기 위해서는 OPT-30B와 350M을 각각 target-draft로 사용하였다.

serving framework로는 vLLM을 사용하였으며, 데이터셋은 HumanEval과 MT-bench를 사용하였다. 두 데이터셋 모두 최대 sequence 길이는 400 토큰까지 존재한다.

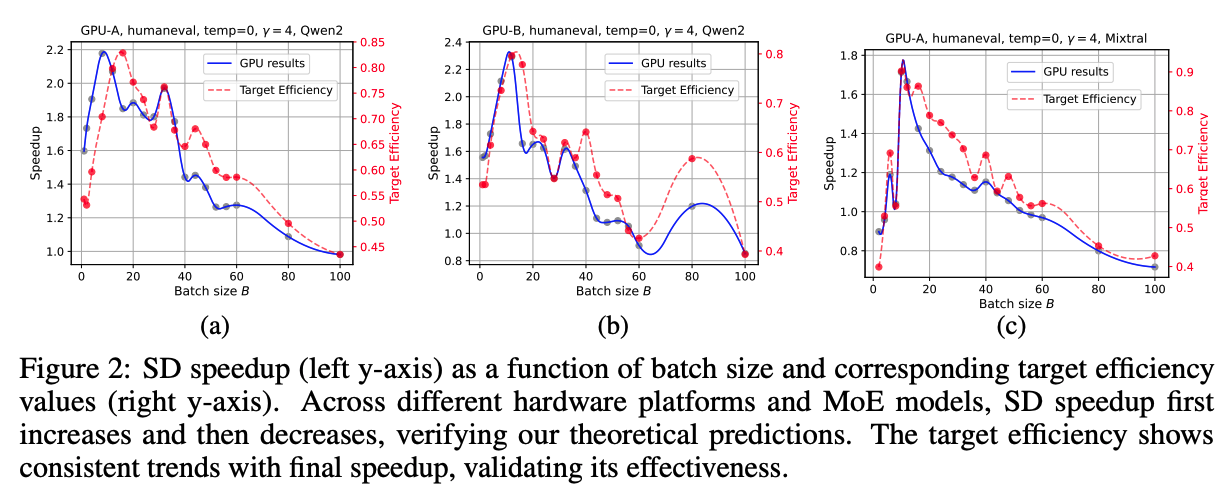
위 그래프는 여러 설정에서의 MoE 모델의 end-to-end 속도 향상률을 나타낸다. batch size가 커질수록 속도 향상은 처음에는 expert의 파라미터 로딩이 포화 상태가 되면서 증가한다. 이 후, compute-bound 구간에 도달하여 다시 감소한다.

추가로 target efficiency의 유효성도 볼 수 있다. target efficiency 또한 speculative decoding으로 인한 속도 향상률과 일관된 추세로 움직이는 것을 볼 수 있다. batch size에 따른 acceptance rate는 작은 범위에서만 변동했으며, 이는 속도 향상률이 급변하는 이유를 설명할 수 있는 정도는 아니라고 보고 있다.

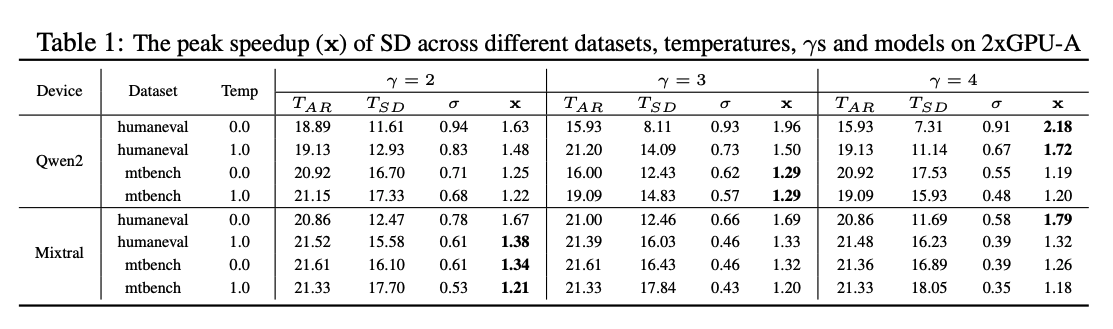
위 표는 batch size 마다 최대 속도 향상 값을 $x$ 로 표기하였다. Qwen-2와 Mixtral 모두 코드 생성이나 낮은 temperature에서 더 큰 속도 향상을 보였는데, 이는 target 모델이 더 예측 가능한 패턴을 선호하기 때문이다. 이 표를 fig 2 그래프와 함께 보면 다음 2가지를 확인 할 수 있다.

더 높은 ridge point를 가진 GPU일수록 더 큰 속도 향상을 보인다. 이는 검증 단계에서 더 많은 연산 유닛을 사용 할 수 있기 때문이다.
GPU의 수를 확장하면 절대적인 실행 시간( $T_{AR},\ T_{SD}$ )은 줄어들지만, speculative decoding 속도 향상 비율은 약간 감소한다. 이는 큰 target 모델이 GPU parallelism의 이점을 얻지만, 작은 draft 모델은 단일 GPU를 사용하기 때문에 상대적으로 forward pass 비용이 커지기 때문이다.

위 그래프는 target efficiency를 기준으로 MoE 모델과 dense 모델을 비교한 결과이다. dense 모델의 경우, batch size를 키울 수록 지속적으로 target efficiency가 감소하는 반면, MoE는 증가 이후에 감소하는 경향이 발생했다.

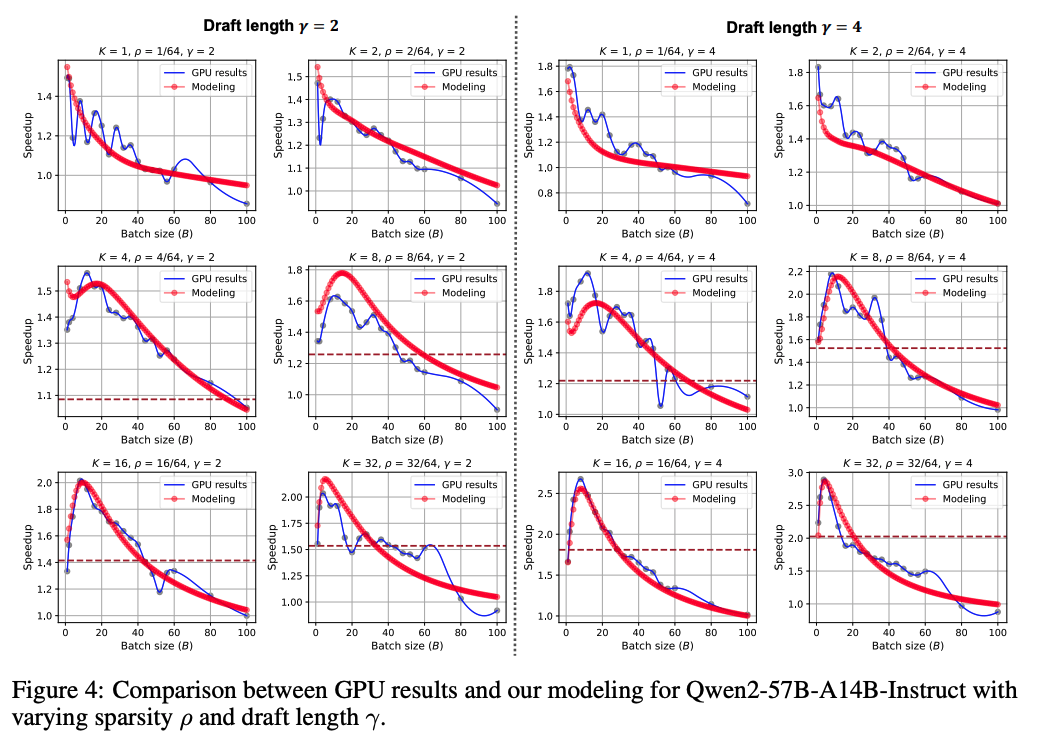
위 그래프는 MoE의 sparsity가 sepculative decoding 가속에 영향을 미치는지 평가하기 위한 그래프이다. Qwen-2 MoE 모델에서 토큰 당 활성화 되는 expert 수인 $K$ 값을 변화 시켰다. 이를 직접 변경하는 경우, 학습 없이 target 모델의 성능과 speculative decoding의 정확도 값인 $\sigma$ 에 영향을 준다. 그렇기 때문에 속도 향상 수치를 보정하기 위해 다음과 같은 비율을 추가하였다고 한다.

Calibrated\ speedup = raw\ speedup \times \frac{\sigma_{K=8}}{\sigma_{K}}

그 결과, 위 그래프로부터 3가지 발견을 하였다.

모델링의 결과가 sparsity( $\rho$ )와 draft 길이( $\gamma$ )가 달라져도 일관된 경향을 보인다.
$K$ 값이 작은 매우 sparse한 MoE의 경우, 속도 향상이 계속 감소 되는 추세를 보인다. 극단적으로 sparse한 경우, FFN 비율이 비정상적으로 낮은 경우가 된다. 그래서 FFN의 memory-bound 특성이 유의미하게 드러나지 않기 때문이다.
정상적인 범위에서 MoE이 더 sparse 할수록, memory-bound에서 compute-bound로 전환 되는 시점이 지연된다.

위 그래프에서 sparsity를 나타내는 $\rho$ 값이 작을수록 최대 속도 향상이 나타나는 batch size가 더 커진다. 또한 속도 향상이 특정한 감소 임계값 이상 (갈색 점선)을 유지하는 batch size 구간이 더 넓어진다.

결론 및 고찰

MoESD의 내용을 요약하자면, 결국 MoE의 expert가 가지는 특성에서 기인하는 memory-bound와 compute-bound를 이용하면 중간 크기의 batch size 정도에서는 speculative decoding이 먹힌다는 내용이였다. 다만 이 논문의 약점은 KV cache의 크기가 모델의 파라미터 크기에 비해 상대적으로 작은 경우를 전제로 하고 있다. KV cache가 문제가 되는 상황은 MagicDec에서 분석이 되었는데, 내가 기억하기로는 MagicDec의 타겟이 MoE는 아니여서 이러한 점이 개선이 필요할 것으로 보인다.

아직까지 회사에서 팀 내에 MoE를 많이 분석한 기록이 없다. 그래서 다른 팀원분이랑 다음주부터 MoE를 좀 더 프로파일링 해봐야 이 논문의 모델링 방식이 KV cache가 큰 상황에서도 먹히는지 확인해야 할 것 같다.

Hyunjoon Jeong

ML System 개발자 입니다.

이전 포스트

[ICML'24] EAGLE: Speculative Sampling Requires Rethinking Feature Uncertainty

다음 포스트