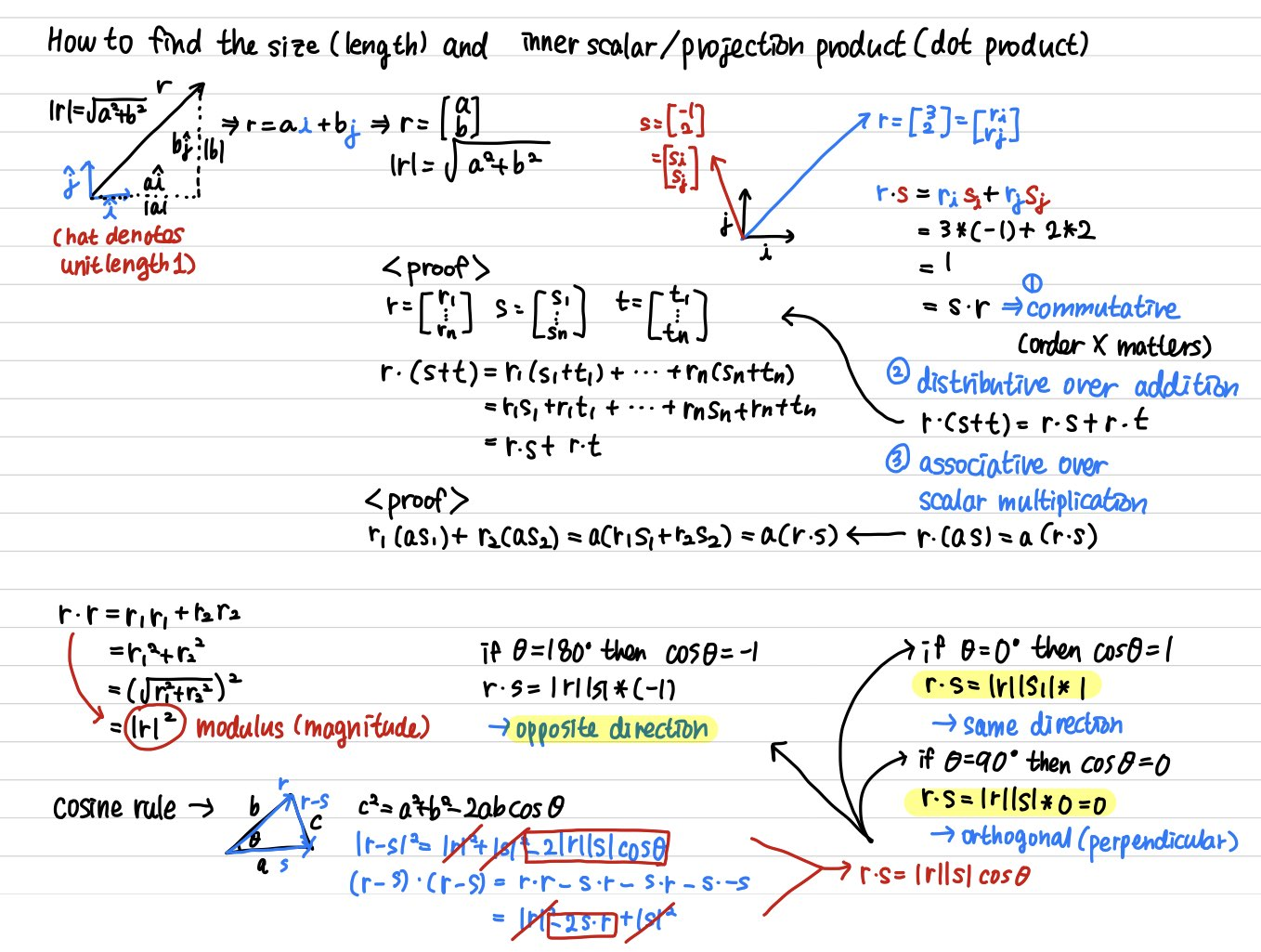
2주차에서는 벡터에 대한 각종 연산, 기저변환(change of basis), 선형독립(linear independence) 등에 관한 내용을 다룬다.
DISCLAIMER: 아래 내용은 오로지 Coursera 강의를 토대로 제가 이해한 대로 정리한 것이기 때문에 부정확하거나 설명이 그닥 친절하지 않은 부분이 있을 수도 있습니다.
벡터의 크기(size/length)
벡터의 크기를 구하는 방법을 알아보자. 벡터 r = [ a b ] r = \begin{bmatrix} a \\ b \end{bmatrix} r = [ a b ] i i i j j j 기저벡터(basis vector) 를 이용하여 r = a i + b j r=ai+bj r = a i + b j 단위벡터(unit vector) 인 경우, 벡터의 크기는 우리에게 친숙한 피타고라스의 정리를 활용하여 ∣ r ∣ = a 2 + b 2 |r|=\sqrt{a^2+b^2} ∣ r ∣ = a 2 + b 2
여담으로 학부에서 공부했을 때는 삿갓 모양의 기호인 hat(^)을 머리 위에 쓴 벡터도 있고 없는 벡터도 있어서 혼란스러웠는데, 해당 강의에서는 hat을 쓴 벡터(e.g., i ^ \hat i i ^ j ^ \hat j j ^
벡터의 내적(dot product)
벡터의 내적(dot product)을 구하려면 벡터에서 대응되는 각 성분끼리 곱한 다음 더해주면 된다.r = r i + r j r=r_i+r_j r = r i + r j s = s i + s j s=s_i+s_j s = s i + s j r r r s s s
r ⋅ s = r i s i + r j s j r \cdot s=r_i s_i+r_j s_j r ⋅ s = r i s i + r j s j
r = [ 3 2 ] r = \begin{bmatrix} 3 \\ 2 \end{bmatrix} r = [ 3 2 ] s = [ − 1 2 ] s = \begin{bmatrix} -1 \\ 2 \end{bmatrix} s = [ − 1 2 ] r ⋅ s = 3 × ( − 1 ) + 2 × 2 = 1 r \cdot s=3\times(-1)+2\times2=1 r ⋅ s = 3 × ( − 1 ) + 2 × 2 = 1
교환법칙(commutative law) : r ⋅ s = s ⋅ r r \cdot s=s \cdot r r ⋅ s = s ⋅ r 덧셈에 대한 분배법칙(distributive law) : r ⋅ ( s + t ) = r ⋅ s + r ⋅ t r \cdot (s+t)=r \cdot s+r \cdot t r ⋅ ( s + t ) = r ⋅ s + r ⋅ t
증명 r = [ r 1 ⋮ r n ] r= \begin{bmatrix} r_1 \\ \vdots \\ r_n\end{bmatrix} r = ⎣ ⎢ ⎢ ⎡ r 1 ⋮ r n ⎦ ⎥ ⎥ ⎤ s = [ s 1 ⋮ s n ] s = \begin{bmatrix} s_1 \\ \vdots \\ s_n\end{bmatrix} s = ⎣ ⎢ ⎢ ⎡ s 1 ⋮ s n ⎦ ⎥ ⎥ ⎤ t = [ t 1 ⋮ t n ] t= \begin{bmatrix} t_1 \\ \vdots \\ t_n\end{bmatrix} t = ⎣ ⎢ ⎢ ⎡ t 1 ⋮ t n ⎦ ⎥ ⎥ ⎤ r ⋅ ( s + t ) = r 1 ( s 1 + t 1 ) + r 2 ( s 2 + t 2 ) + ⋯ + r n − 1 ( s n − 1 + t n − 1 ) + r n ( s n + t n ) = r 1 s 1 + r 1 t 1 + r 2 s 2 + r 2 t 2 + ⋯ + r n − 1 s n − 1 + r n − 1 t n − 1 + r n s n + r n + t n = r ⋅ s + r ⋅ t \begin{aligned} r \cdot (s+t) &= r_1(s_1+t_1)+ r_2(s_2+t_2) + \dots + r_{n-1}(s_{n-1}+t_{n-1}) + r_n(s_n+t_n) \\ &= r_1s_1+r_1t_1+r_2s_2+r_2t_2+\dots+r_{n-1}s_{n-1}+r_{n-1}t_{n-1}+r_ns_n+r_n+t_n \\ &= r \cdot s+r \cdot t\end{aligned} r ⋅ ( s + t ) = r 1 ( s 1 + t 1 ) + r 2 ( s 2 + t 2 ) + ⋯ + r n − 1 ( s n − 1 + t n − 1 ) + r n ( s n + t n ) = r 1 s 1 + r 1 t 1 + r 2 s 2 + r 2 t 2 + ⋯ + r n − 1 s n − 1 + r n − 1 t n − 1 + r n s n + r n + t n = r ⋅ s + r ⋅ t 곱셈에 대한 결합법칙(associative law) : r ⋅ ( a s ) = a ( r ⋅ s ) r \cdot(as)=a(r \cdot s) r ⋅ ( a s ) = a ( r ⋅ s )
증명 r = [ r 1 r 2 ] , s = [ s 1 s 2 ] r= \begin{bmatrix} r_1 \\ r_2\end{bmatrix}, s= \begin{bmatrix} s_1 \\ s_2\end{bmatrix} r = [ r 1 r 2 ] , s = [ s 1 s 2 ] r ⋅ ( a s ) = r 1 ( a s 1 ) + r 1 ( a s 2 ) = a ( r 1 s 1 + r 2 s 2 ) = a ( r ⋅ s ) \begin{aligned} r \cdot(as) &= r_1(as_1)+r_1(as_2) \\ &= a(r_1s_1+r_2s_2) \\ &= a(r \cdot s) \end{aligned} r ⋅ ( a s ) = r 1 ( a s 1 ) + r 1 ( a s 2 ) = a ( r 1 s 1 + r 2 s 2 ) = a ( r ⋅ s )
동일한 벡터에 대한 내적은 해당 벡터 크기의 제곱과 값이 같다.
r ⋅ r = ∣ r ∣ 2 r \cdot r = |r|^2 r ⋅ r = ∣ r ∣ 2
r ⋅ r = r 1 r 1 + r 2 r 2 = r 1 2 + r 2 2 = ( r 1 2 + r 2 2 ) 2 = ∣ r ∣ 2 \begin{aligned} r \cdot r &= r_1r_1+r_2r_2 \\ &= r_1^2+r_2^2 \\ &= (\sqrt{r_1^2+r_2^2})^2 \\ &= |r|^2 \end{aligned} r ⋅ r = r 1 r 1 + r 2 r 2 = r 1 2 + r 2 2 = ( r 1 2 + r 2 2 ) 2 = ∣ r ∣ 2
Cosine Rule : c 2 = a 2 + b 2 − 2 a b cos θ c^2=a^2+b^2-2ab\cos\theta c 2 = a 2 + b 2 − 2 a b cos θ
a a a b b b c c c s s s r r r r − s r-s r − s
∣ r − s ∣ 2 = ∣ r ∣ 2 + ∣ s ∣ 2 − 2 ∣ r ∣ ∣ s ∣ cos θ |r-s|^2=|r|^2+|s|^2-2|r||s|\cos\theta ∣ r − s ∣ 2 = ∣ r ∣ 2 + ∣ s ∣ 2 − 2 ∣ r ∣ ∣ s ∣ cos θ
또한 위에서 알아본 것처럼 동일한 벡터에 대한 내적은 해당 벡터 크기의 제곱과 같다는 것과 벡터의 덧셈에 대한 분배법칙을 활용하여 다음과 같이도 표현할 수 있다.
( r − s ) ⋅ ( r − s ) = r ⋅ r − s ⋅ r − r ⋅ r + s ⋅ s = ∣ r ∣ 2 − 2 s ⋅ r + ∣ s ∣ 2 \begin{aligned} (r-s)\cdot(r-s) &= r \cdot r - s \cdot r - r \cdot r + s \cdot s \\ &= |r|^2-2s \cdot r+|s|^2 \end{aligned} ( r − s ) ⋅ ( r − s ) = r ⋅ r − s ⋅ r − r ⋅ r + s ⋅ s = ∣ r ∣ 2 − 2 s ⋅ r + ∣ s ∣ 2
∣ r − s ∣ 2 = ( r − s ) ⋅ ( r − s ) |r-s|^2=(r-s)\cdot(r-s) ∣ r − s ∣ 2 = ( r − s ) ⋅ ( r − s ) − 2 ∣ r ∣ ∣ s ∣ cos θ = − 2 s ⋅ r -2|r||s|\cos\theta=-2s \cdot r − 2 ∣ r ∣ ∣ s ∣ cos θ = − 2 s ⋅ r
r ⋅ s = ∣ r ∣ ∣ s ∣ cos θ r \cdot s=|r||s|\cos\theta r ⋅ s = ∣ r ∣ ∣ s ∣ cos θ
이렇게 나온 공식을 활용하면 내적을 통해 두 벡터 사이에 있는 각(θ \theta θ
두 벡터가 같은 방향이면(θ = 0 ° \theta=0\degree θ = 0 ° cos θ = 1 \cos\theta=1 cos θ = 1 r ⋅ s = ∣ r ∣ ∣ s ∣ r \cdot s=|r||s| r ⋅ s = ∣ r ∣ ∣ s ∣
두 벡터가 서로 직각(orthogonal )으로 만난다면(θ = 90 ° \theta=90\degree θ = 9 0 ° cos θ = 0 \cos\theta=0 cos θ = 0 r ⋅ s = 0 r \cdot s=0 r ⋅ s = 0
두 벡터가 서로 반대 방향이면(θ = 180 ° \theta=180\degree θ = 1 8 0 ° cos θ = − 1 \cos\theta=-1 cos θ = − 1 r ⋅ s = − ∣ r ∣ ∣ s ∣ r \cdot s=-|r||s| r ⋅ s = − ∣ r ∣ ∣ s ∣
삼각함수 복습하기
삼각함수를 워낙 오랜만에 접해서 그런지 값이 바로바로 생각 안 나는 바람에 조금 애를 먹었다.
θ \theta θ 0 ° 0\degree 0 ° 30 ° 30\degree 3 0 ° 45 ° 45\degree 4 5 ° 60 ° 60\degree 6 0 ° 90 ° 90\degree 9 0 ° sin \sin sin 0 0 0 1 2 \frac{1}{2} 2 1 2 2 \frac{\sqrt{2}}{2} 2 2 3 2 \frac{\sqrt{3}}{2} 2 3 1 1 1 cos \cos cos 1 1 1 3 2 \frac{\sqrt{3}}{2} 2 3 2 2 \frac{\sqrt{2}}{2} 2 2 1 2 \frac{1}{2} 2 1 0 0 0 tan \tan tan 0 0 0 1 3 \frac{1}{\sqrt{3}} 3 1 1 1 1 3 \sqrt{3} 3 ∞ \infty ∞
필요할 때 참고해서 보면 될 것 같다.
필기 첨부
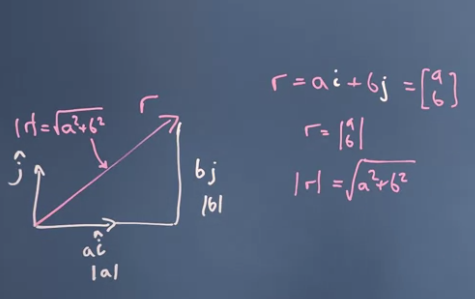
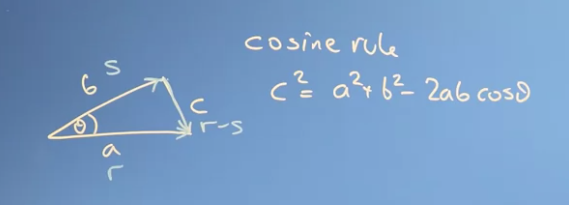삼각형의 각 변 , , 를 각각 , , 라는 벡터로 표현해서 코사인 공식에 대입하면 다음과 같다.
