Linear Algebra - 2주차 2/2

2주차에서는 벡터에 대한 각종 연산, 기저변환(change of basis), 선형독립(linear independence) 등에 관한 내용을 다룬다.

DISCLAIMER: 아래 내용은 오로지 Coursera 강의를 토대로 제가 이해한 대로 정리한 것이기 때문에 부정확하거나 설명이 그닥 친절하지 않은 부분이 있을 수도 있습니다.

---

사영벡터(projection)

사영(projection)은 쉽게 이해하자면 벡터의 그림자 같은 것이라고 생각하면 된다고 한다. 사실 학부 강의에서 배웠을 때에는 projection이라는 게 어떠한 의미를 지니는지 충분히 이해하지 못한 채 공식을 외우는 데만 신경을 썼다. 그래서 시험이나 과제에서 응용 문제가 나오면 잘 풀지 못했다.
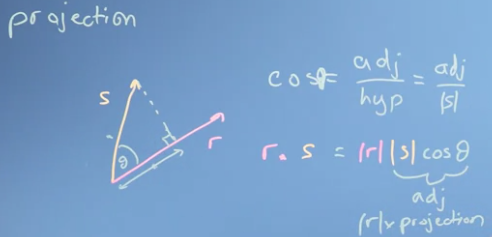벡터 $s$를 벡터 $r$에 수직으로 내리면 직각삼각형이 생긴다. 이렇게 생긴 삼각형에 대해서 우리가 고등학교 때 배운 코사인 공식을 대입해보자.

$\cos\theta=\frac{adj}{hyp}=\frac{adj}{|s|}$ (cf. $adj$: adjacent, $hyp$: hypotenuse)

즉 $adj=|s|\cos\theta$로 표현할 수 있다. 여기서 adjacent변의 길이는 곧 사영벡터의 크기와 같다.
그리고 $r$와 $s$의 내적은 $r \cdot s=|r||s|\cos\theta$이므로 여기에 공식을 대입하면 다음과 같은 결과가 나온다.

scalar projection: $|s|\cos\theta=\frac{r \cdot s}{|r|}$

그리고 사영벡터 자체를 구하려면 여기에 단위벡터(unit vector)인 $\frac{r}{|r|}$를 다음과 같이 곱해주기만 하면 된다. 즉 단위벡터는 벡터 $r$의 방향을 나타낸다고 생각하면 될 것 같다.

vector projection: $\frac{r \cdot s}{|r|}\frac{r}{|r|}=(\frac{r \cdot s}{r \cdot r})r$

이렇게 구한 사영벡터를 이용하여 우리는 기저변환이라는 것을 할 수 있다.

---

기저변환(change of basis)

기저벡터 $\hat{e_1}=\begin{bmatrix} 1 \\ 0\end{bmatrix}$, $\hat{e_2}=\begin{bmatrix} 0 \\ 1\end{bmatrix}$와 이 기저벡터들로 표현된 벡터 $r=3\hat{e_1}+4\hat{e_2}=\begin{bmatrix} 3 \\ 4\end{bmatrix}$가 있다.
여기에 새로운 기저벡터 $b_1=\begin{bmatrix} 2 \\ 1\end{bmatrix}$, $b_2=\begin{bmatrix} -2 \\ 4\end{bmatrix}$를 추가해보자. 여기서 기저변환(change of basis)을 통해 벡터 $r$를 새로운 기저벡터 $b_1$, $b_2$에 대하여 표현되도록 바꿀 수 있다.
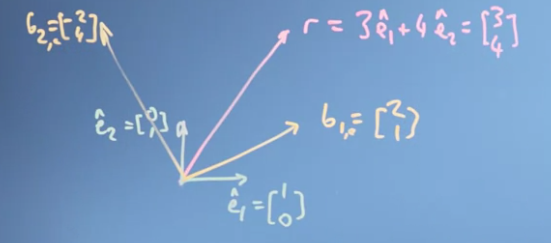우선 $b_1$, $b_2$에 벡터 $r$를 사영시킨 scalar projection 값을 구한다. $b_1$에 $r$를 사영시킨 scalar projection 값은 다음과 같다.

$\frac{r \cdot b_1}{{|b_1|}^2}=\frac{3\times2+4\times1}{2^2+1^2}=\frac{10}{5}=2$

$b_1$에 $r$을 사영시킨 사영벡터는 $2b_1$이 된다.

마찬가지로 $b_2$에 $r$를 사영시킨 scalar projection 값을 구해보자.

$\frac{r \cdot b_2}{{|b_2|}^2}=\frac{3\times(-2)+4\times4}{(-2)^2+4^2}=\frac{10}{20}=\frac{1}{2}$

$b_2$에 $r$를 사영시킨 사영벡터는 $\frac{1}{2}b_2$가 된다.

따라서 벡터 $r$는 기저변환을 통해 $r=2b_1+\frac{1}{2}b_2$로 표현할 수 있다. 여기에 $b_1$, $b_2$의 값을 대입하면 기존에 $e$에 대해 표현한 벡터 $r$값인 $r=\begin{bmatrix} 3 \\ 4\end{bmatrix}$이 나오는 것을 확인할 수 있다.

---

기저(basis)와 선형독립(linear independence)

기저(basis)란, 벡터 공간에서 다음과 같은 성질을 가지는 n개의 벡터의 집합이다.

• 벡터들은 서로 선형독립적(linearly independent)하다. 즉, 서로 선형조합(linear combination)이 아니어야 한다. (대충 다른 벡터들을 조합해서 나머지 한 벡터를 만들 수 없어야 한다는 뜻)

  • 두 개의 벡터 $b_1$, $b_2$가 있을 때 $a_1b_1+a_2b_2\neq0$이어야 linearly independant하다.
  • 마찬가지로 세 개의 벡터 $b_1$, $b_2$, $b_3$가 있을 때 $b_3 \neq a_1b_1+a_2b_2$이어야 linearly independant하다.

• 벡터들은 공간을 span해야 한다. 공간이 n차원일 때, 서로 선형독립인 n개의 벡터가 존재해야 한다. 만약에 3차원 공간에서 2개의 벡터만 linearly independent한 상태라면 해당 기저는 2차원까지만 span한다고 볼 수 있다.

강의에서는 기저벡터들이 orthonormal한 게 이상적이라고 한다. 여기서 orthonormal하다는 것은 집합에 있는 모든 벡터가 서로 직교(orthogonal)하고 단위벡터(unit vector)라는 뜻이다. 아... 맨날 헷갈렸었는데 orthonormal이 ortho+normal이라는 걸 오늘 처음 깨달았다... 바보 된 기분 허허

---

필기 첨부