Maximum Likelihood Estimator (MLE)

MLE는 무엇이고, 왜 중요한가?

---

• 데이터를 가장 잘 설명하는 확률 분포의 파라미터 값을 찾는 것이 목적이다.

⇨ 중요한 이유

---

1. 실생활 문제 해결에 유용하다. 현실세계에서의 문제는 정확한 규칙을 알 수 없기 때문에 관찰된 데이터를 통해 가장 가능성이 높은 가설을 만들어내야 한다.
   1. 예를 들어, 병원에서 환자의 질병을 진단할 때 환자 증상을 보고 어떤 질병에 걸렸을 가능성이 높은지 추정할 때 사용할 수 있다.
2. 가장 그럴듯한 답을 찾아준다. MLE는 관찰된 데이터를 기준으로 이 데이터가 이렇게 나왔을 가능성이 가장 높은 상황을 찾아준다. 즉, 데이터의 패턴을 가장 잘 설명하는 확률 분포의 파라미터를 찾아주는 것이다.
   1. 예를 들어 주사위를 던져서 [1,2,2,3] 이 나왔다면, MLE는 해당 데이터를 가장 잘 설명하는 주사위의 숫자 분포를 추정해주는 것이다.

기본 개념

---

1. 수학적 정의

---

---

• LIkelihood 함수
• 파라미터 theta에서 데이터 X가 관찰될 확률을 나타냄

---

• MLE로 추정된 최적의 파라미터 값
• MLE는 Likelihood 값을 최대화하는 방향으로 파라미터를 조정한다.

2. Likelihood 함수의 의미 - 확률 밀도 함수(PDF)와 차이점

---

• 이산 사건 (셀 수 있는 사건): 확률
• 연속 사건: 우도 함수, 확률 밀도 함수
  - 연속사건에서 특정 사건의 확률은 모두 0이다. (1/∞)
  - 특정 사건이 나올 확률은 의미가 없어서 다른 방법을 생각해야한다.
  - 사건이 특정 구간에 속할 확률을 구하는 것이 그 대안!

1. 확률 밀도 함수
   1. 모델 파라미터를 고정된 값으로 보고 데이터를 변수로 간주한다. → 주어진 파라미터 값에서 특정 데이터가 관측될 확률(밀도)을 나타낸다.
   2. 특정 구간에 속할 확률 = 그래프에서 특정 구간에 속한 넓이
2. 가능도 (Likelihood)
   1. 데이터를 고정된 값으로 보고 모델 파라미터를 변수로 간주한다. → 주어진 데이터에서 특정 파라미터 값이 얼마나 가능성 있는지를 나타낸다.
   2. 특정 사건이 일어날 가능성을 비교하기 위함
   3. 확률 분포 함수의 y값으로 구할 수 있다.
      1. 이산 사건: 가능도 = 확률
      2. 연속 사건: 가능도 ≠ 확률, 가능도 = PDF 값

• 요약

  특징	PDF	Likelihood Function
  입력	데이터, 고정된 파라미터	고정된 데이터, 변화하는 파라미터
  출력	특정 데이터 포인트의 확률 밀도	특정 파라미터 값이 데이터에 대해 가질 가능도
  목적	데이터의 확률 분포 설명	데이터를 가장 잘 설명하는 파라미터 추정
  적분값	정의역에서 적분값이 항상 1	적분값이 1일 필요 없음
  활용	데이터의 확률 계산	파라미터 추정, 모델 학습

3. Log-Likelihood 함수

---

• 로그 연산을 사용하는 이유는 계산을 더 편하게 하기 위해서이다.
• 문제점: Likelihood는 곱셈 연산으로 표현된다. 우도 함수는 데이터 X의 모든 관찰값에 대한 확률을 곱한 값. 곱셈은 숫자가 많아질수록 계산량이 기하급수적으로 증가하기 때문에 복잡성 문제가 발생한다.
  $L(\theta \mid X) = \prod_{i=1}^{n} f(x_i \mid \theta)$
• 해결: 로그 함수로 변환 → 곱셈 대신 덧셈으로 변환되므로 계산이 더 간단해진다.

⇨ 예시: 동전 던지기 10번 중 7번이 앞면

---

1. PDF

   1. 목적: p(동전 앞면이 나올 확률)이 주어질 때, 앞면이 7번 나올 확률 구하기

      

2. Likelihood Function

   1. 목적: p(동전 앞면이 나올 확률)을 변화시켜서 데이터를 가장 잘 설명하는 P를 찾기. 즉, 앞면이 7번 나온 실험 결과를 가장 잘 설명할 수 있는 p 찾기.

   2. 이항분포의 MLE 유도하는 과정과 같다.

      

계산식 유도

---

• 위의 예시 문제 풀 때 계산식 유도를 이미 해서 .. 유도 흐름만 정리하겠음 !
• 유도 과정
  1. 우도 함수를 정의
  2. 데이터를 가장 잘 설명하는 파라미터(θ)를 찾기 위해 L(θ∣X)를 최대화하기
  3. 로그우도함수로 변환: 계산의 편리함을 위해서 해주는 것
  4. 로그우도함수를 θ에 대해 미분하기
  5. 미분값을 0으로 설정하여 θ를 추정하기

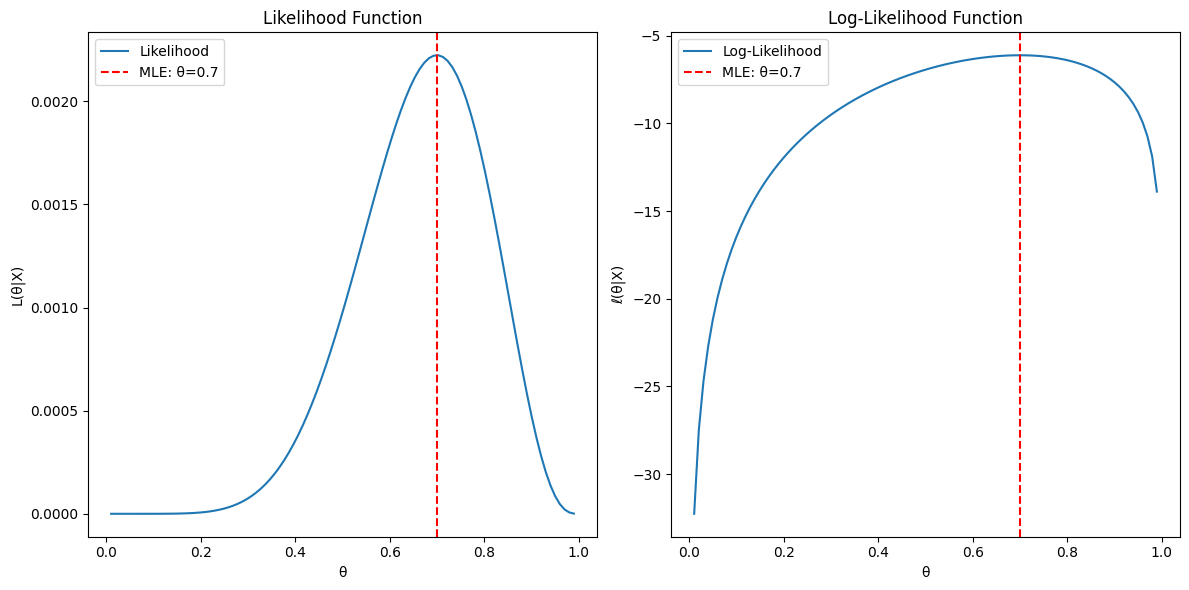
그래프 설명

---

• 위의 예시 문제에 대한 시각적인 설명 추가

  

  • 각각 그래프는 위에서 정의한 식을 matplotlib 코드로 작성하여 그렸다.
  • 코드: MLE Graph Ex. - binomal distrubution
    • google drive로 연결되어요 ..ㅎ.ㅎ

MLE 특징³

---

• 큰 샘플일수록 정확도가 높다.

  • 반대로 작은 데이터에서 편향된 결과를 도출할 가능성이 있다.

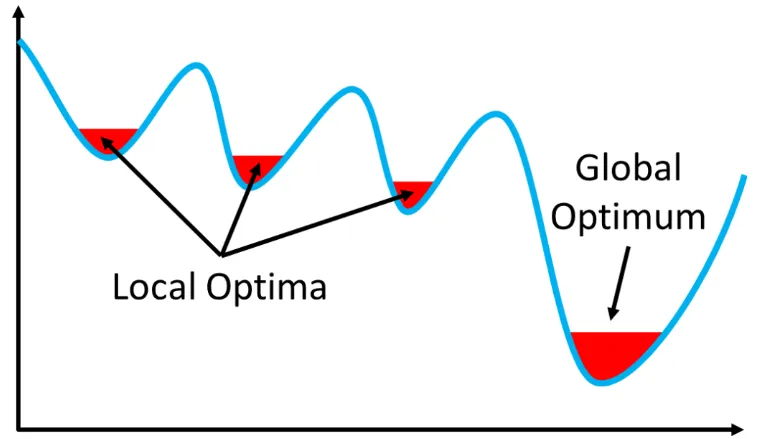
• Local Optimum에 빠질 가능성이 있다.

  • 우도 함수가 복잡한 형태일 경우에 최적화 과정에서 전역 최대값(Global Maximuum) 대신에 국소 최대값(Local Maximum)에 머무를 가능성이 있다.
  • 복잡한 모델에서는 우도 함수가 여러 개의 봉우리를 가질 수 있다.

Python을 사용한 간단 MLE 구현 (scipy 패키지 사용)⁴

---

⇨ 1 정규분포의 평균(μ)을 추정하는 과정

---

• 위에서 도출해낸 식을 코드로 적용하면 된다.
• 코드: MLE Graph Ex. - Normal Distribution

추가 공부

---

• MLE와 MAP 비교
  • MLE는 prior(사전확률)를 고려하지 않음
  • MAP는 prior를 포함하는 베이즈 접근법
• Robust MLE
  • 편향을 줄이는 다양한 기법 소개

참고자료

---

1. 기초통계 개념 정리
2. Likelihood Function: 우도함수 - pdf와의 차이점
3. 머신러닝-Local-optimum이란
4. 파이썬 - 유용한 함수 scipy의 optimize, minimize 활용해보기
5. 최대우도법(MLE) - 공돌이의 수학정리노트 (Angelo's Math Notes)