신경망의 학습에는 여러 기술들을 사용할 수 있다. 가중치 매개변수의 최적값을 탐색하는 최적화 방법, 가중치 매개변수 초깃값, 하이퍼파라미터 설정 방법 등을 사용한다면 범용성을 갖춘 성능이 좋은 모델을 만들 수 있다고 한다. 신경망의 효율성과 정확성을 높힐 수 있는 방법 중 하나인 최적화에 대해 간략하게 예습을 해보기로 했다.
💛 Optimization(최적화)와 Optimizer(최적값)
신경망의 학습은 손실함수의 값을 최대한 낮추는 매개변수를 찾는 것이었다. 이는 매개변수의 최적값을 찾는 방법에 대해 생각해봐야하며 이러한 최적값을 찾는 문제를 푸는 것을 최적화라고 한다.
신경망은 보통 빅데이터를 크고 복잡한 모델에 넣는 것이기 대문에 매개변수들이 만드는 공간은 넓고 복잡하며 사용자가 그 내부를 보기 어려운 black box 모델이기 때문에 최적화를 쉽게할 수 있는 방법을 찾기는 어렵다.
지금까지 적절한 매개변수의 값을 찾는 방법은 매개변수의 기울기를 구하는 미분을 사용하는 것이었다.
경사하강법을 사용하여 매개변수의 기울기를 구해 기울어진 방향으로 매개변수 값을 업데이트하는 일을 반복하여 최적값에 도달하는 것이다.
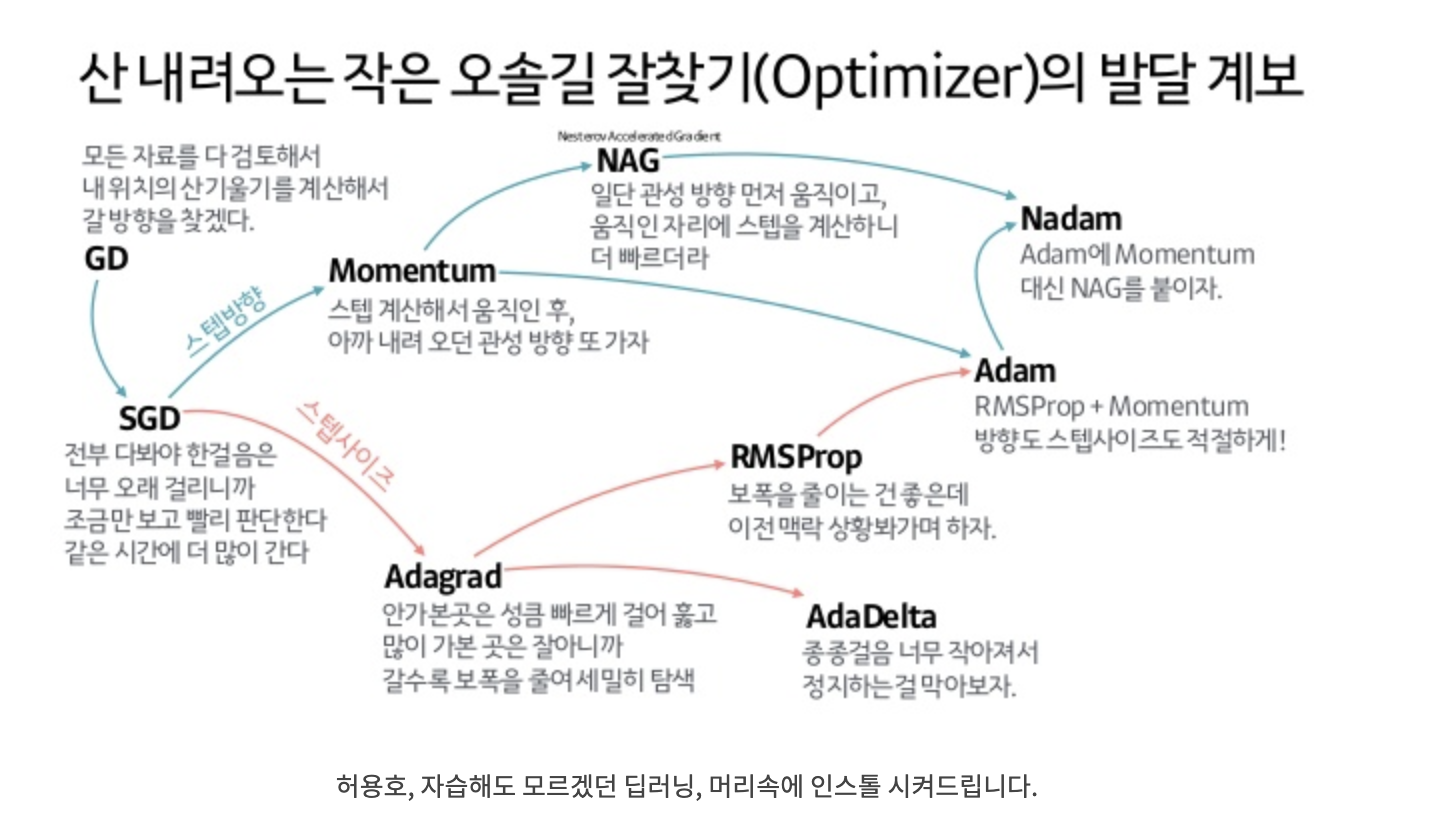
SGD(Stochastic Gradient Decent, 확률적 경사하강법)
훈련데이터셋에서 무작위로 한 개의 샘플 데이터셋을 추출하고 그 샘플에 대해서만 기울기를 계산하는 것
(전체 훈련 데이터셋을 대상으로 학습하는 것은 리소스를 비효율적으로 사용하는 것이고 매개변수 업데이트 수가 적다는 것은 랜덤하게 뽑힌 시작 위치의 가중치 수가 적다는 것이므로 local minimum 현상이 발생할 확률도 높다고 볼 수 있다.)
장점
- 샘플 데이터셋에 대해서만 경사(gradient)를 계산하므로 반복해서 다뤄야할 데이터 수가 매우 적어 학습속도가 빠르다.
- 샘플 데이터 한 개만을 대상으로 경사를 계산하기 대문에 메모리 소모량이 매우 낮아 빅데이터에서도 학습이 용이하다.
단점
- 무작위로 추출된 샘플에 대해서 경사를 구하기 때문에 배치 경사하강법보다 불안정하게 움직인다.
- 손실함수가 최솟값에 다다를 때까지 불안정하게 움직이다보니 학습이 진행되면 근접하게 움직이지만 global minimum(최적해)에 도달하지 못할 가능성이 있다.
이러한 단점을 보안하기 위해 mini-batch gradient descent(미니 배치 경사하강법)이 등장하였다.
SGD(with momentum)
momentum이란 이동방향에 관성을 주는 방법이다.
현재 기울기가 향하는 방향과 별개로 그동안 하강해온 방식을 기억하면서 그 방향으로 일정 정도를 추가적으로 이동하는 방식으로 SGD보다 덜 불안정하게 움직이면서 목적지 근처에 도달하는 방식이다.
adagrad(adaptive Gradient)
변수를 업데이트할 때마다 각각의 변수마다 스텝 사이즈를 다르게 설정해서 이동하는 방식
지금까지 많이 변한 변수들은 목적지 가까이에 있을 확률이 높기 때문에 세세하게 조정하고자 스텝 사이즈를 작게 설정하고 변하지 않았던 변수들은 목적지에서 멀리있을 확률이 높기 때문에 스텝 사이즈를 크게 하여 많이 변하도록 하는 것이다.
학습을 많이 진행하면 스텝이 너무 작아서 조정이 오히려 어렵게 될 수 있다는 단점이 있다.
RMSProp
adagrad의 단점을 보완한 방법으로 상대적인 크기의 차이를 유지하면서 스텝 사이즈를 설정하여 움직여서 스텝 사이즈가 지나치게 작아져서 멈추는 것을 방지하는 방법이다.
adam
adam은 adagrad의 단점을 보완한 RMSProp과 momentum을 합친 알고리즘이다.
가장 많이 쓰이고 인기있는 최적화 방법으로 가중치를 업데이트하는 최적화 방법이라고 할 수 있다.
참고 블로그 1
참고 블로그 2
참고 블로그 3: 수식 참고하기
❓ 옵티마이저들의 장단점과 차이에 대해 이해하기
