신경망에서 과적합을 방지하기 위한 방법(Regularization Strategies)
과적합(overfitting)과 그 원인
신경망(neural network)는 매개 변수가 상당히 많은 복잡한 모델이다.
이러한 모델은 훈련데이터에 쉽게 과적합되는 경향이 있다.
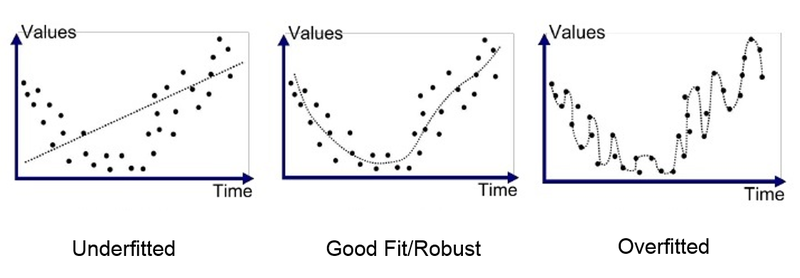
과적합은 우측의 그림처럼 데이터에 과하게 적합하게 학습이 이루어진 경우로 모델의 학습과정에서 과적합이 일어나면 모델의 성능이 떨어지게 된다.
과적합의 원인 또한 다양하다.
데이터의 수가 너무 적거나 feature의 수가 너무 많거나 간단한 데이터에 지나치게 복잡한 모델을 사용하거나 그 반대이거나...이처럼 다양한 관점에서 과적합이 일어나는 만큼 다양한 관점에서 과적합을 방지하기 위한 method들이 있다.
일반적인 regularization 방법들을 정리해보고자 한다.
+- 💛 모델에 적용하는 Regularization Strategies : Dropout
| : 테스크가 예상외로 간단한데 모델이 복잡한 경우 간단한 모델을 사용하거나 층을 줄이거나 노드를 줄일 수 있다.
+- 💛 데이터에 하는 Regularization Strategies : 전처리, 데이터 증강
| : EDA로 데이터 전처리를 하고 필요시 이상치 제거, 데이터를 부족하면 데이터 증강으로 보완한다.
+- 💛 손실함수에 하는 Regularization Strategies : L1, L2 Norm
| : weight decay
+- 💛 가중치에 하는 Regularization Strategies : weight constraint
|
+- 💛 학습 및 추론 방식에 하는 하는 Regularization Strategies :Early stopping, 앙상블/베깅, 교차검증
: early stopping으로 학습을 일찍 종료하거나 앙상블/베깅을 사용하여 모델을 여러 개 섞어 투표를 하거나 교차 검증으로 추론 방식에 제한을 걸 수 있다.
신경망에 적용하는 일반적인 Regularization Strategies
🥕 early stopping (조기 종료)
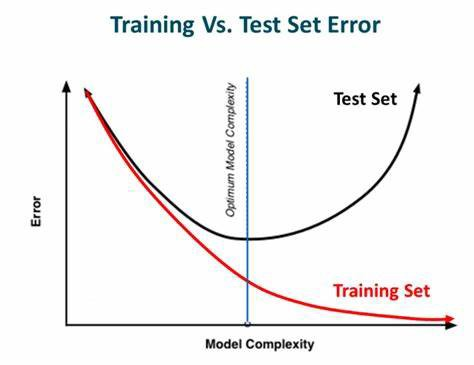
모델은 훈련데이터셋으로 학습을 한다. 하지만 훈련 데이터셋에 맞춰 오류를 줄일수록 과적합의 위험이 커지게 되는데 조기 종료를 통해 훈련데이터에 대한 손실은 줄어들지만 검증데이터에 대한 손실이 증가한다면 학습을 종료하도록 하는 방식이다.
🥕 weight decay (가중치 감소)
가중치의 값이 크다면 과적합의 위험도 커진다. 가중치를 감소하려면 손실함수(cost function)에 가중치와 관련된 항을 추가하여 값이 지나치게 커지지 않도록 조정할 수 있다. 이는 학습 과정에서 큰 가중치에 대해서느 그에 상응하는 큰 패널티를 부과하여 오버피팅을 억제하는 방법이다. 오버피팅은 가중치 매개변수의 값이 커서 발생하는 경우가 많기 때문이다.
가중치 항을 어떻게 추가할지에 따라 L1 Regularization, L2 Regularization으로 나뉜다.
주로 회귀 문제에서 많이 쓰였다. (cf. ridge regression)
강력한 규제이기 때문에 underfit을 불러일으킬 수도 있어서 과적합도 막지 못하고 정확도도 낮으니까 모델의 성능 자체를 낮출 수도 있다는 단점이 있다.
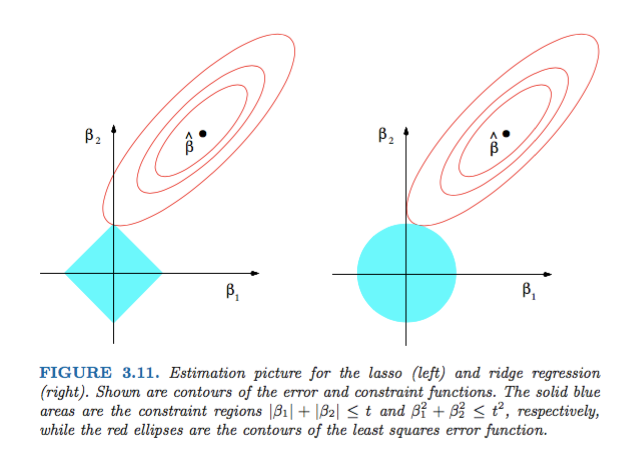
신경망 학습의 목표는 손실 함수의 값을 줄이는 것이다. 이 때 L2 norm(가중치의 제곱 노름)을 손실함수에 더하게 되면 가중치가 커지는 것을 방지할 수 있는 것이다. 가중치를 W라고 한다면 L2 norm에 따른 가중치 감소는 W가 된다.
는 정규화의 세기를 조절하는 하이퍼파라미터로 가 클수록 큰 가중치에 대한 패널티가 커진다.
이 W를 손실함수에 더해주면 가중치가 감소하게 되는 것이다.
W에서 는 W의 미분결과인 W를 조정하는 역할의 상수이다.
가중치 감소는 모든 가중치 각각의 손실함수에 W를 더한다.
따라서 가중치의 기울기를 구하는 계산에서는 그동안의 역전파법에 따른 결과에 정규화 항을 미분한 W를 더한다.
🥕 weight constraint (가중치 제한)
가중치 감소와 유사한 목적을 달성하기 위해 특정 가중치를 제거하거나 범위를 제한하는 방법이다.
유사한 방법으로 weight decusion과 weight restriction이 있다.
🥕 dropout
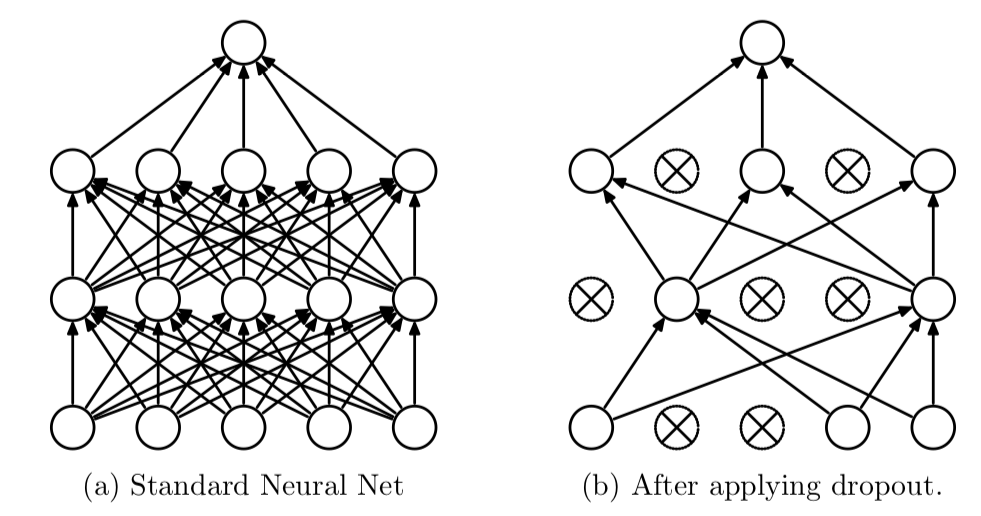
dropout은 iteration마다 레이어 노드 중 일부를 사용하지 않으면서 학습을 진행하는 방법이다.
이를 통해 매번 다른 노드가 학습되기 때문에 전체 가중치가 과적합되는 것을 방지할 수 있는 것이다.
코드 구현 상의 장점이라고 할 수 있는 사소한 부분은 dropout과 batchnorm이 switch가 가능하다는 것이다.
