본 포스트 내용은 ML 기초 쌓기 #2에서 이어지는 내용입니다.
ML의 기법과 관련된 알고리즘의 종류는 수없이 많다고 합니다.
대표적으로 지도 학습(Supervised learning)과 비지도 학습(Unsupervised learning)으로 구분됩니다.
이 둘의 차이점은 학습 결과에 대한 사전 지식이 존재의 유무입니다. 학습 결과에 대한 사전 지식이 있으면 지도 학습 기법을 활용하면 예측과 분류가 가능하고, 학습 결과에 대한 사전 지식이 없으나 가지고 있는 데이터를 통해 유의미한 지식을 얻고자 하면 비지도 학습 기법을 활용하면 될 것 입니다.
3. 지도 학습(Supervised Learning)
Reference
지도학습에는 원하는 결과 데이터인 레이블(Lable = 종속변수)이 포합되어야 합니다.
전형적으로는 분류(Classification)가 전형적인 지도 학습 작업입니다.
다른 작업으로는 예측 변수(Predictor Variable)인 특성(Feature)를 이용해서 최종적인 결과를 예측하는 회귀(Regression)가 있습니다.
일부 회귀 알고리즘은 분류 작업에도 사용할 수도 있습니다. 예를 들어 로지스틱 회귀(Logistic Regression)을 통해 클래스에 속할 확률을 구합니다.
가장 널리 쓰이는 지도 학습의 알고리즘은 다음과 같습니다.
- K-최근접 이웃 : K-Nearest Neighbors
- 선형 회귀 : Linear Regression
- 로지스틱 회귀 : Logistic Regression
- 결정 트리 : Decision Tree
- 랜덤 포레스트 : Random Forest
- 점진적 부스팅 머신: GBM(Gradient boosting Machine)
- 서포트 벡터 머신 : SVM(Support Vector Machine)
- 신경망 : Neural Network
3.1 KNN(K-Nearest Neighbors)
Reference
K-Nearest Neighbors, 최근접 이웃법은 새로운 데이터를 입력 받았을 때 가장 가까이 있는 것이 무엇이냐를 중심으로 새로운 데이터의 종류를 정해주는 알고리즘입니다.
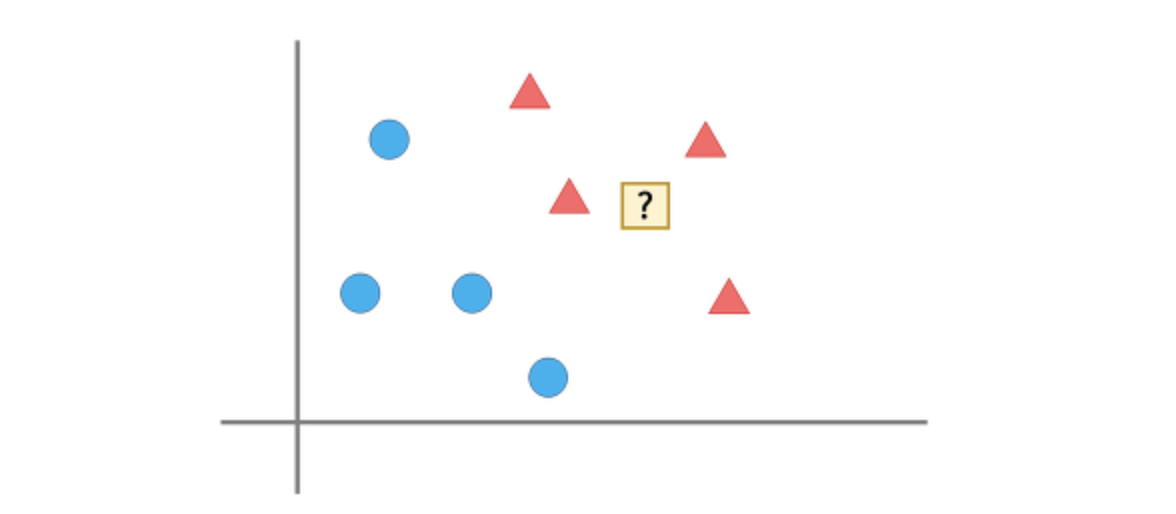
위의 그림에서 ?는 무엇을까요? 주변에 있는 것이 세모이기 때문에 세모라고 판단하는 간단하고 직관적인 알고리즘 입니다.
하지만 단순하게 가장 가까이 있는 것과 같게 하는 것은 옳은 분류가 아닙니다.
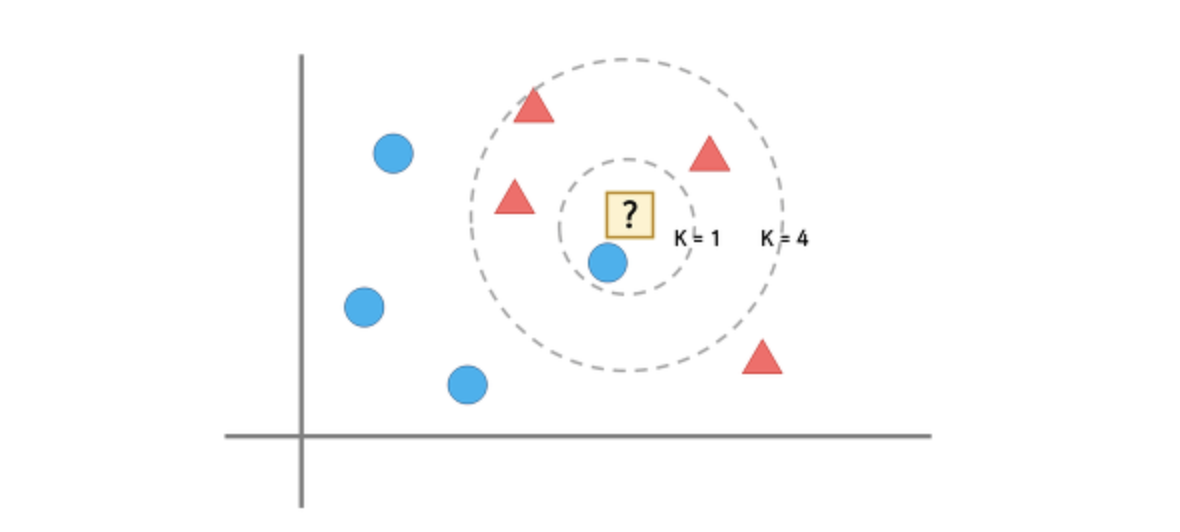
앞선 예시와 같이 판단하면 ?는 동그라미가 되겠지요. 하지만 저희는 멀리 넓게 보고 있기 때문에 부적절하다는 것이 한번에 느껴집니다.
그렇기에 KNN에서는 가장 가까운 것이 아니라 주변에 있는 것들의 개수를 보고 가장 많은 것을 판단하여 고르는 방식을 사용합니다.
K=1일 때는 ?는 동그라미지만, K=4일 때는 ?는 세모입니다.
이 때의 문제는 K가 몇일 때 가장 좋을 것인가 입니다. 일반적으로 K 값이 커질수록 분류에서 이상치의 영향이 줄어들지만 분류를 못하게 되는 상황이 발생합니다. 따라서 보통은 총데이터의 제곱근 값을 사용하
고 있습니다.
3.2 Linear Regression
Reference
가장 기본적이고 널리 사용되는 학습 알고리즘 중 하나입니다.
Linear Regression, 선형 회귀는 가장 적합한 회귀선을 사용하여 종속 변수 Y: Target와 하나 이상의 독립 변수 X 간의 관계를 모델링 합니다.
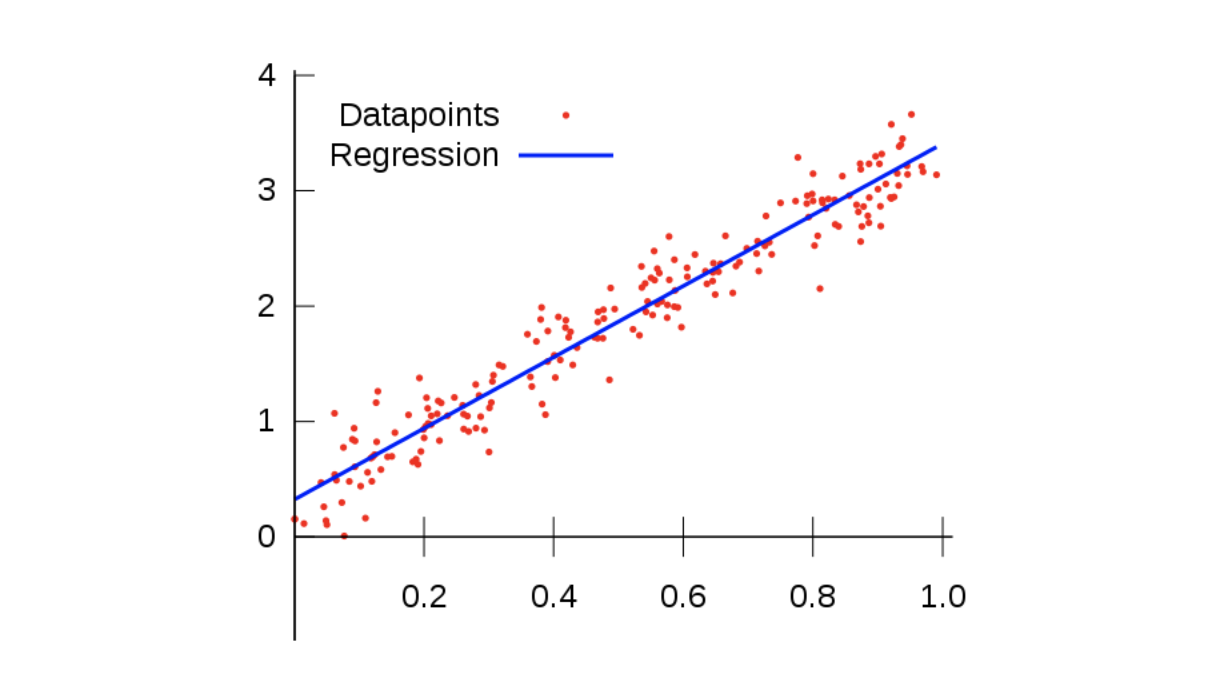
출처 - https://medium.com/simple-ai/linear-regression-intro-to-machine-learning-6-6e320dbdaf06
위의 그림처럼 기존의 데이터들과의 오차가 가장 적은 회귀선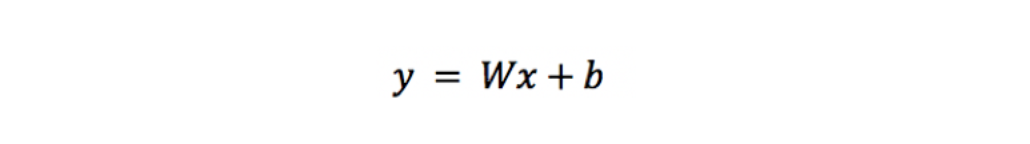
을 구함으로써 X를 입력 받을 때 Y의 값(Target)을 예측할 수 있습니다.
결국 y = Wx + b의 회귀선에서 예측 값과 실제 값의 오차가 가장 작은 W값과 b값을 구하고 얻어낸 회귀선에 근거하여 예측 값을 도출합니다.
W값과 b값을 구하는 방법인 Cost function(비용함수 = Loss function)과 최적화(Optimization)은 Reference 포스트에 잘 정리가 되어있으니 해당 포스트를 통해 확인해주세요.
3.3 Logistic Regression
Reference
Logistic Regression, 로지스틱 회귀는 일반 적인 회귀 분석과 동일하게 독립 변수와 종속 변수간의 관계를 함수로 나타내서 예측 모델에 사용하는 것입니다.
하지만, 선형 회귀 분석과는 다르게 종속 변수가 범주형 데이터응 대상으로 하며 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 댸문에 일종의 분류 기법으로도 볼 수 있습니다.
분류 문제에서 선형 회귀를 사용한다면
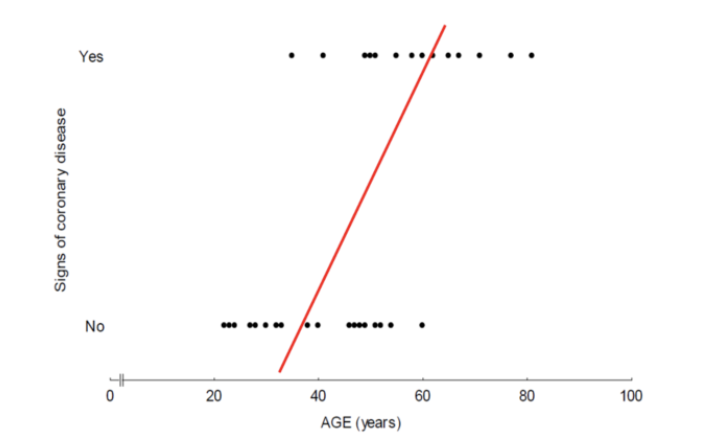
이러한 이상한 그래프가 생성될 것입니다.
위와 같은 문제가 발생하는 이유는 종속변수Y는 0 또는 1의 값으로만 이루어져 있기 때문에 중간 범주가 없으며 연속적인 수가 아니기 때문에 0과 1이 서로 바뀌어 분류되어도 큰 문제가 발생되지 않습니다.
이처럼 종속변수 Y가 범주형 변수일 때 문제를 해결하기 위해서 로지스틱 회귀 모델이 제안되었습니다.
로지스틱 회귀는 이향형 또는 다항형이 될 수 있습니다.
- 이항형 : 성공, 실패와 같이 2개의 카테고리가 존재하는 것을 의미합니다.
- 다항형 : 이김, 짐, 비김 등과 같이 3개 이상의 카테고리가 존재하는 것을 의미합니다.
동일한 점은 모든 카테고리로 분류될 확률의 합은 1입니다.
더 자세한 내용은 참고 포스트인 ratsgo's blog - 로지스틱 회귀 포스트로 가주세요.
3.4 Decision Tree
Reference
Decision Tree는 데이터를 분석해서 데이터 사이에 존재하는 패턴을 예측 가능한 규칙의 조합으로 나타내는 것입니다. 이 모양이 나무와 같다고 해서 의사 결정 나무(Decision Tree)라고 부르게 되었습니다.
참고 포스트에서 든 예시를 보니 이해가 잘 되었습니다.
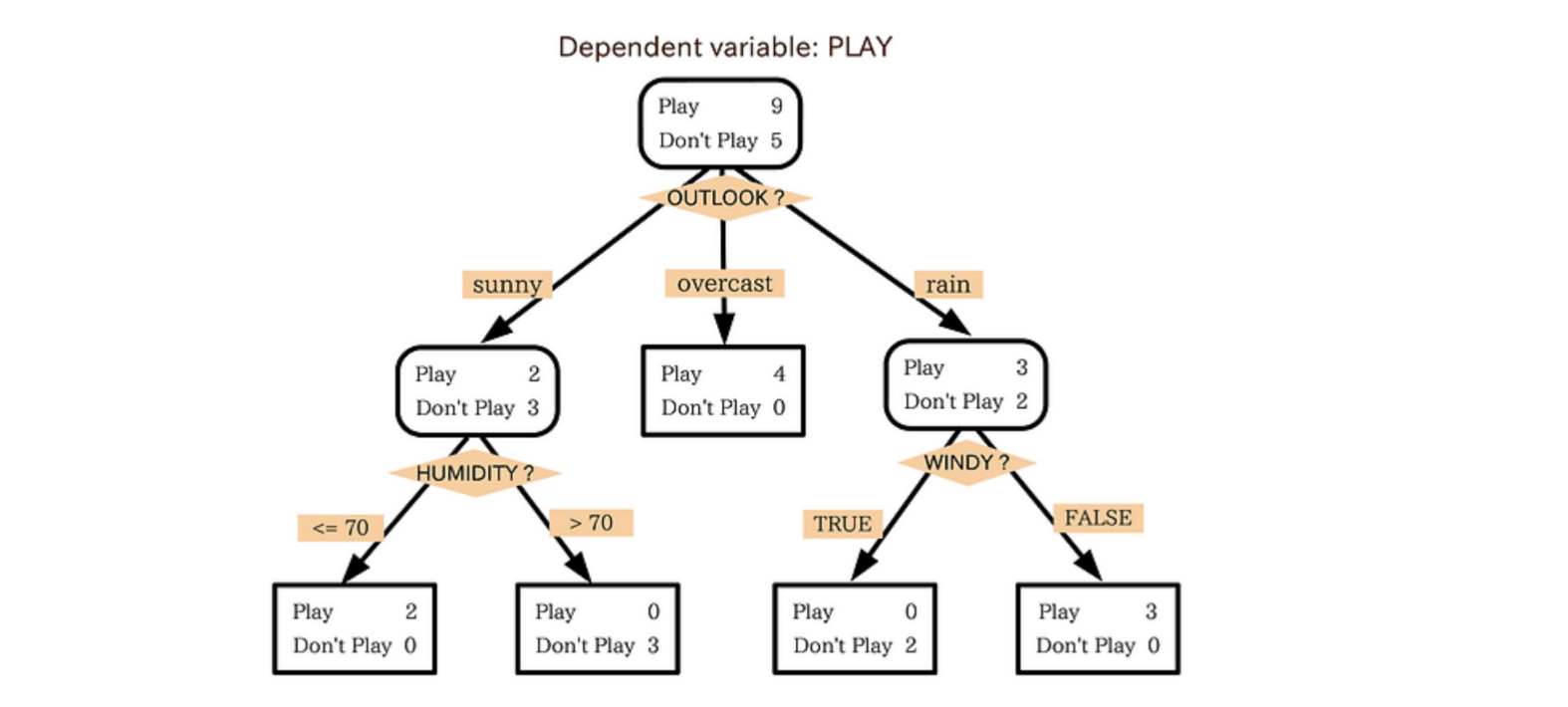
위의 예시는 운동경기가 열렸다면 PLAY = 1, 그렇지 않다면 PLAY = 0으로 하는 binary Classification 문제입니다. 그림을 해석해보면 HUMIDITY > 70 이거나 WINDY == TRUE 일 때는 PLAY = 0, 그 외에는 PLAY = 1 입니다.
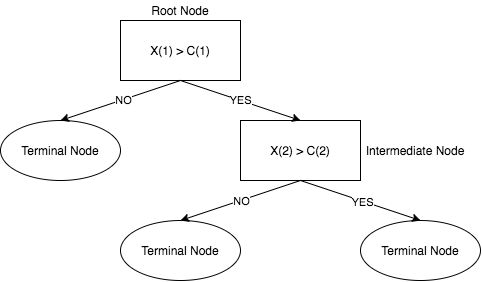
Decision Tree를 일반화 한 그림은 위의 그림과 같습니다.
전체적으로 보면 나무를 뒤집어 놓은 듯한 모양이죠?
초기 지점은 Root Node이고 분기가 거듭될 수록 그에 해당하는 데이터는 줄어듭니다.
Decision Tree는 Classification과 Regression 모두 가능합니다. 연속형 수나 범주 모두 예측할 수 있습니다.
더 자세한 내용은 참고 포스트를 통해 확인해주세요.
3.5 Random Forest
Reference
Baek Kyun Shin - 머신러닝 - 5. 랜덤 포레스트(Random Forest)
텐서 플로우 블로그 - 2.3.6 결정 트리의 앙상블
Random Forest는 Decision Tree가 모인 숲(Forest)입니다.
Decision Tree 하나만으로 머신러닝을 할 수 있지만 데이터셋에 대해 Overfitting이 되는 문제가 발생할 수 있습니다. 이 때, 여러 개의 Decision Tree를 통해 문제를 해결할 수 있습니다.
예를 들어 건강에 대한 위험도를 예측하기 위해서는 굉장히 많은 요소(Feature)들을 고려해야 합니다. 키, 나이, 성별, BMI, 음주 여부 등 굉장히 많은 요소가 있겠죠.
위의 예시에서 대충 Feature가 30개라고 할 때, Decision Tree의 가지는 꽤나 많아질 것입니다. 이 때 Overfitting 문제가 발생할 수 있습니다.
30개 중 랜덤의 5개 Feature로 Decision Tree를 생성하고, 다른 5개로 생성하고 총 6개의 Decision Tree를 생성하면 각 Tree마다 예측값이 나옵니다.
6개의 Decision Tree가 예측한 값들 중에 가장 많이 나온 값을 최종 예측값으로 정하는 것입니다.
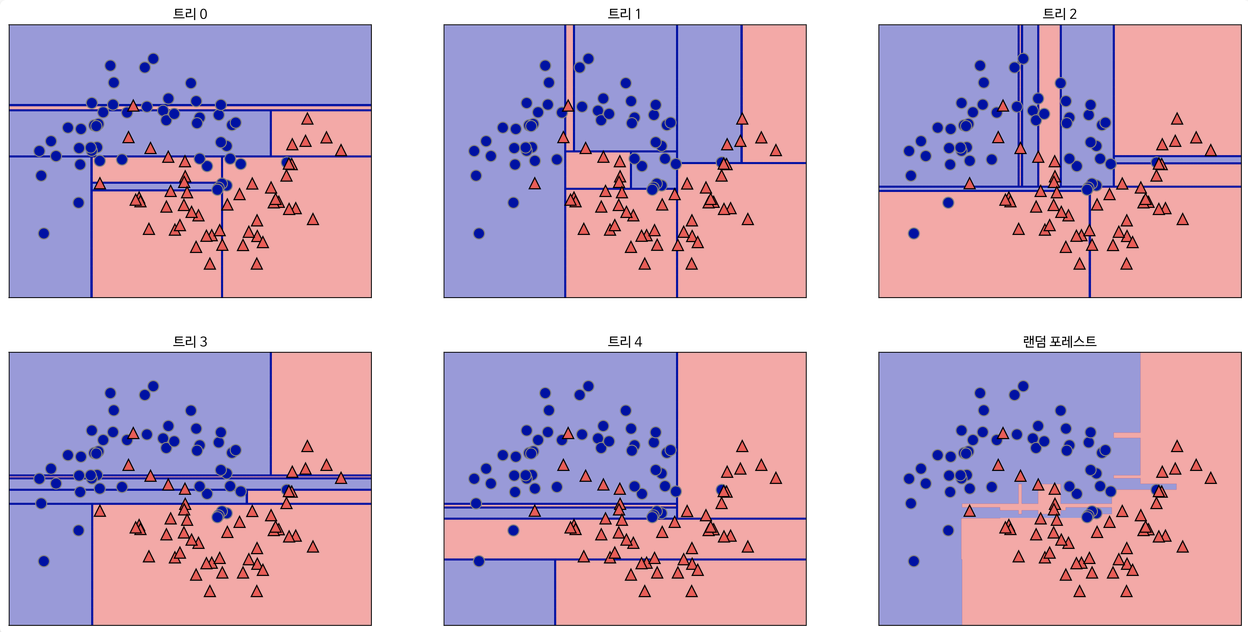
위의 그림은 5개의 Decision Tree 통해 Random Forest를 진행한 결과를 시각화한 것 입니다.
5개의 Decision Tree의 예측 경계와 5개의 예측 경계를 통해 Random Forest된 최종 예측 경계를 보면 최종 예측 경계가 훨씬 부드러운 것을 볼 수 있습니다.
3.6 GBM : Gradient Boosting Machine
Reference
Deep Play - Gradient Boosting Algorithm의 직관적인 이해
텐서 플로우 블로그 - 2.3.6 결정 트리의 앙상블
점진적 부스팅 머신 일명 GBM은 회귀 분석 또는 분류 분석을 수행할 수 있는 예측모형입니다. 그 중 Ensemble 방법론 중 Boosting 계열에 속합니다.
특히, Random Forest와 같이 기본적으로 Decision Tree를 기반으로 Ensemble하는데 차이점은 Gradient Boosting은 무작위성(Random)이 없이 사전에 강력한 가지 치기를 통해 이전 트리의 오차를 보완하는 방식으로 순차적으로 트리를 생성합니다.
따라서, 트리가 많이 추가될 수록 성능이 좋아집니다.
Ensemble에 대해서는 추후 더 자세하게 공부해보겠습니다.
여기서 Boosting은 예를 들어 분류기 A, B, C가 있을 때 각 모델은 Accuracy = 0.3 정도입니다. 분류기 A, B, C를 결합하면 더 높은 정확도인 Accuracy = 0.7 정도 나오는 것이 기본적인 Ensemble의 원리입니다.
여기서 A 분류기를 먼저 만들고 그 정보를 토대로 B 분류기를 만들고 쌓인 정보로 C 분류기를 만듭니다.
최종적으로 만들어진 모든 분류기를 결합해서 최종 모델을 만드는 것이 Boosting입니다.
보다 확실하게 이해하기 위해서는 Residual fitting(잔차 분석)을 통해 이해하는 것이 좋습니다.
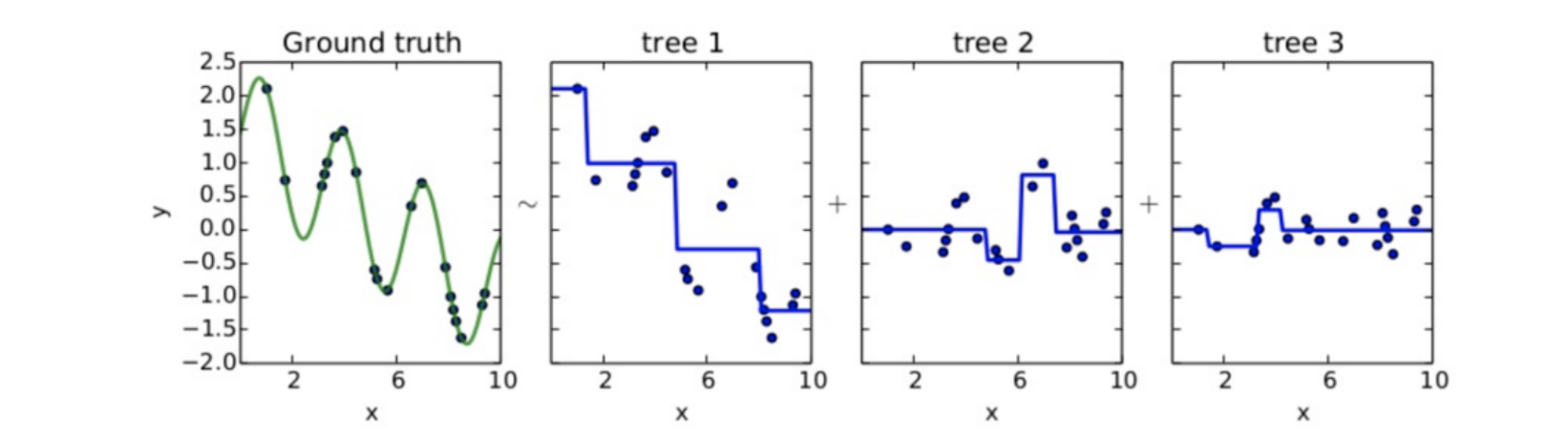
위 그림에서 우측으로 갈 수록 잔차(Residual)가 줄어가는 것을 볼 수 있습니다.
부스팅을 진행할 수록 잔차는 계속 줄어들게 되면서 Train data set을 잘 설명할 수 있는 예측 모형이 만들어 집니다.
하지만, 이런 방식은 bias는 상당히 줄일 수 있어도 과적합(Overfitting)이 발생할 수 있으며 속도가 느리다는 단점이 있습니다.
이러한 Ensemble Boosting Model에서 성능을 더 끌어 올린 여러 모델이 나왔는데 그중 머신러닝 부스팅 알고리즘인 XGBoost 모델이 있습니다.
3.6.1 XGBoost
이 XGBoost의 특징은
- GBM보다 빠릅니다.
- Overfitting 방지 가능 규제가 표함되어 있습니다.
- CART(Classification And Regression Tree)기반입니다. 즉, 분류와 회귀 둘 다 가능합니다.
- Early Stopping을 제공합니다.
추후 머신러닝에 관한 패키지 등을 공부할 때 중점적으로 다루겠습니다.
3.6.2 LightGBM
Reference
이수진의 블로그 - 머신러닝 ensembel lightgbm 알고리즘이란? python 예제와 함께 살펴보자
XGBoost는 GBM에 비해 좋은 성능을 보여주고 비교적 빠르지만 그래도 여전히 학습시간이 느리다는 단점이 이슈입니다.
또한, Hyper Parameter도 많아 Hyper Parameter 튜닝을 하게되면 더 오래 걸린다는 단점이 있습니다.
LightGBM은 위와 같은 XGBoost의 단점을 보완해주기 위해 탄생했습니다. 그리고 GPU까지 지원해준다고 합니다.
LightGMB은 기존의 Gradient Boosting 알고리즘과는 다르게 동작합니다.
기존 Boosting 모델들은 트리의 깊이(Tree Depth)를 줄이기 위해 균형 트리분할(level wise)을 사용했지만 LightGBM은 리프 중심 트리분할(leaf wise)을 진행합니다.
level wise하게 되면 트리의 균형을 잡아주면서 Tree Depth를 줄이기 때문에 추가 연산이 진행되지만 leaf
wise를 하게 되면 균형을 맞추지 않는 대신에 Leaf Node를 지속적으로 분할하면서 진행하게 됩니다.
그리고, 이 Leaf Node를 Max Delta Loss 값을 가지는 리프 노드를 계속 분할해갑니다. 그렇기 때문에 비대칭적이고 Tree Depth가 높은 트리가 생성되지만 동일 Leaf를 생성할 때 Level wise보다 손실을 줄일 수 있다는 것이 장점입니다.
또한, 추후 머신러닝에 관한 패키지 등을 공부할 때 중점적으로 다루겠습니다.
3.7 SVM(Support Vector Machine)
Reference
Support Vector Machine은 주어진 데이터가 어느 카테고리에 속할지 판단하는 이진 선형 분류 모델입니다.
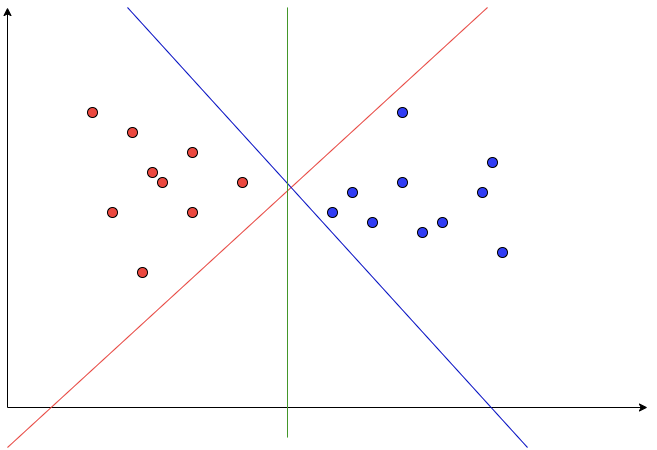
위의 그래프에서 빨간색 점과 파란색 점을 가장 잘 구분하는 선은 바로 빨강, 파랑, 초록중에 초록입니다.
왜냐하면, 선과 점과의 거리(margin)를 가장 최대화하기 때문입니다.
이때, 선과 가장 가까운 포인트(점)를 Support Vector라고 합니다. 즉, margin은 Support Vector와 선 사이의 거리를 의미합니다.
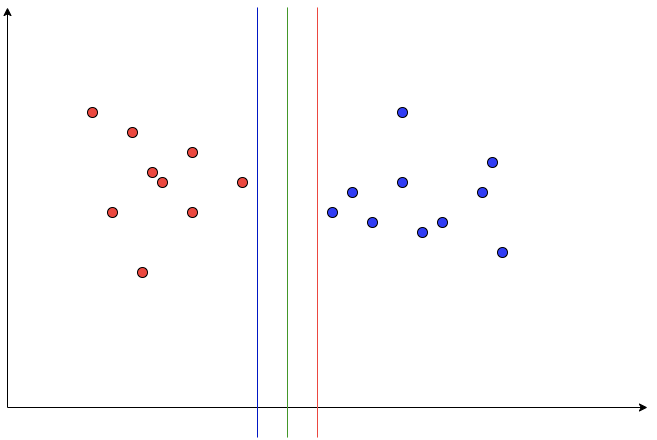
위의 그래프와 같은 경우에는 어떤 선이 가장 적절한 구분선일까요? 초록색 선이 가장 Margin을 최대화하기 때문에 초록색 선입니다.
이렇게 각 Support Vector와의 Margin을 최대화하면 Robustness도 최대화됩니다. 즉, Outlier의 영향을 거의 받지 않는다는 뜻입니다.
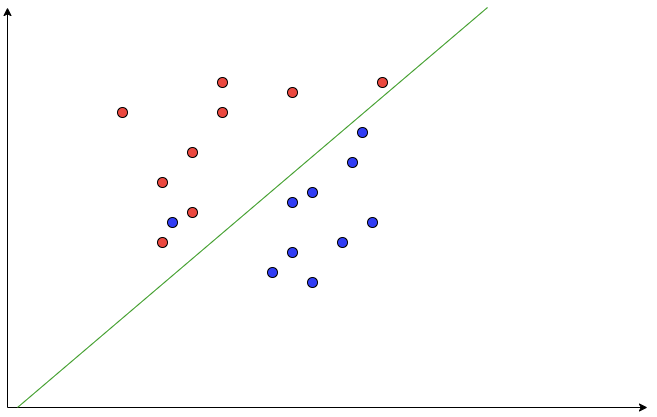
위의 그래프같은 경우 빨간 점 사이에 파란 점이 하나(Outlier) 섞여있습니다.
SVM은 두 데이터를 정확하기 구분하는 선을 찾는 것이 우선이기 때문에 어느정도의 Outlier를 무시하고 최적의 구분선을 찾기 때문에 구분선은 초록색입니다.
Outlier를 무시할 수 없으며 선으로 구분할 수 없는 경우에는 Kernel Trick이라는 방법을 사용합니다.
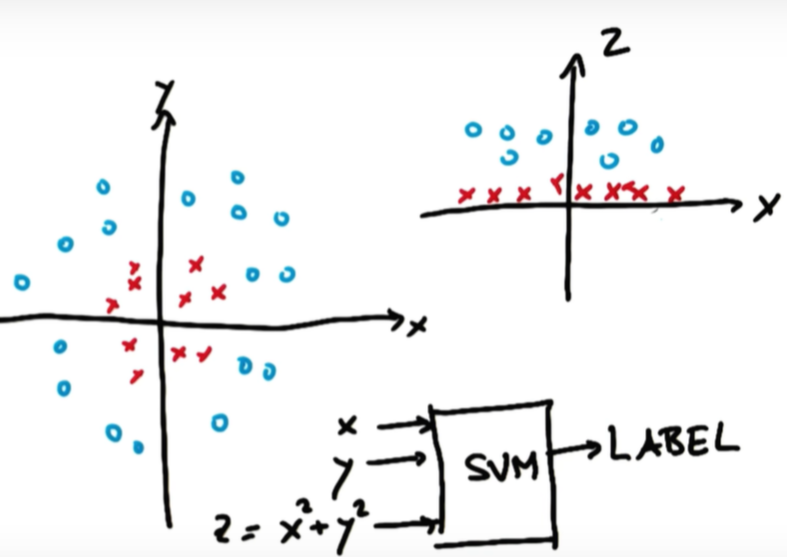
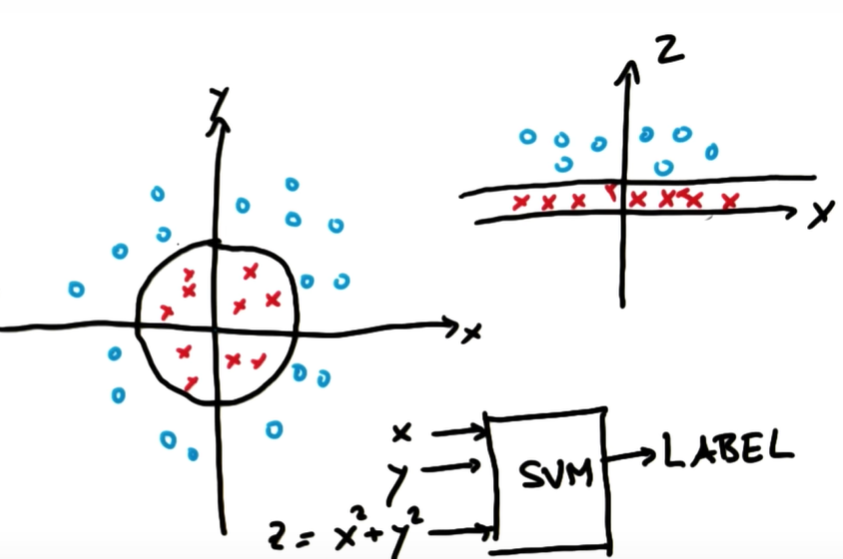
출처: Udacity
위의 그림과 같이 왼쪽 그래프에서는 빨간 점과 파란 점을 구분할 수 있는 선형 구분선은 없습니다. 이때 2차원에서 3차원으로 차원을 변경해주어 오른쪽 그림의 그래프처럼 차원을 이용해 선형인 구분선을 찾는 것입니다.
3.8 Neural Network
신경망의 경우에는 기초 지식조차 매우 방대하기 때문에 추후 자세하기 다루겠습니다.
