
지금은 모두가 Adam optimizer을 당연하게 사용하고 있다. 왜 그런지 Adam의 원리를 보면, 그 이유를 알 수 있지 않을까 하여 이렇게 정리하게 되었다
리뷰하는 "ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION (2015)" 논문은 ICLR 2015 conference paper이고, 마지막 챕터 9. ACKNOWLEDGMENTS 에서 말하듯이 Google Deepmind의 지원하에 연구된 결과를 발표한 논문이다.
0. ABSTRACT

🟡 ADAM에 대해서 한 마디로 요약하자면?
lower-order moments 의 adaptive 추정치를 기반으로,
stochastic objective function 를 최적화하는,
first-order gradient-based (한 번 미분한, 기울기 기반의?) 알고리즘!
lower-order moments
: 저차(저차수) 모멘트
좀 더 정확히는 2개의 moment를 사용하는데,
Adam의 첫번째 moment는 Momentum 알고리즘에서, 두번째 moment는 AdaGrad/RMSProp 알고리즘에서 유도된다.
first-order gradient
: 1차 함수 기울기
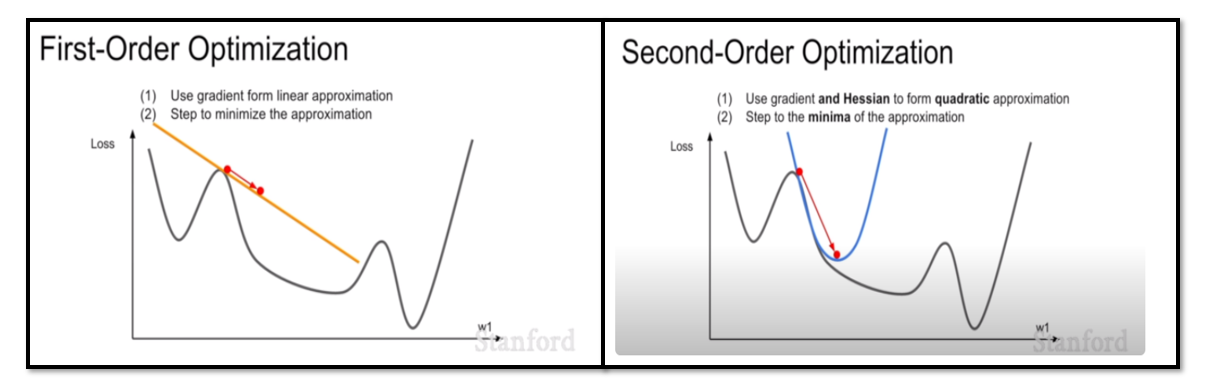
🔖 Reference 설명 추가
- SGD, AdaGrad, RMSProp, Adam은 모두 First-Order Optimization
- 한번 미분한 weight만 optimize에 반영됨
- 그러나 1차 함수 방향(노란색 직선)으로만 optimize하기 때문에 graident 수정이 제한적
이를 보완하기 위해 고차 함수 optimization(오른쪽 그림)이 등장- 그러나 고차 함수 optimization은 역전파를 위해 역행렬을 구할 때, 시간 복잡도가 엄청나게 증가함 (ex : 가중치의 차원이 몇 백만 차원으로 늘어남)
- 이러한 이유로 아직까지는 First-Order Optimization을 사용하고 있음
stochastic object functions
: Loss Function
(mini-batch 방식과 같이 random하게 training sample을 선택함으로써 매번 loss function 값이 달라지는 함수. Ex. MSE, Cross Entropy...))
🟢 ADAM의 장점?
- 구현이 간단
- 효율적인 계산
- 적은 메모리 필요
- gradient의 diagonal rescaling에 invariant

위과 같은 상황에서 gradient 값이 커지거나 작아져도,

이런 계산 과정을 거쳐서, 결론적으로는 위와 같이 Digonal 곱셈으로 graident를 변하게 해도, optimze 과정에서 영향을 미치지 않는다는 것이다.
- 큰 사이즈의 데이터와 파라미터인 상황에서도 적합함
- 노이즈가 심하거나 sparse gradient 상황에서도 적합합
- 직관적인 하이퍼 파라미터로 적당한 튜닝만이 필요함
🔵 다른 Optimizer와 비교한다면?
기존의 optimizer(AdaGrad, RMSProp, AdaDelta,,)들과 비교했을때도 매주 좋은 성능을 보인다.
⚪ (추가) Adam의 변종, AdaMax
추라고 Adam의 변종인 AdaMax에 대한 내용도 후반 챕터에서 말한다.
1. INTRODUCTION

🔴 Object functions(loss function)은 stochastic(확률적)!
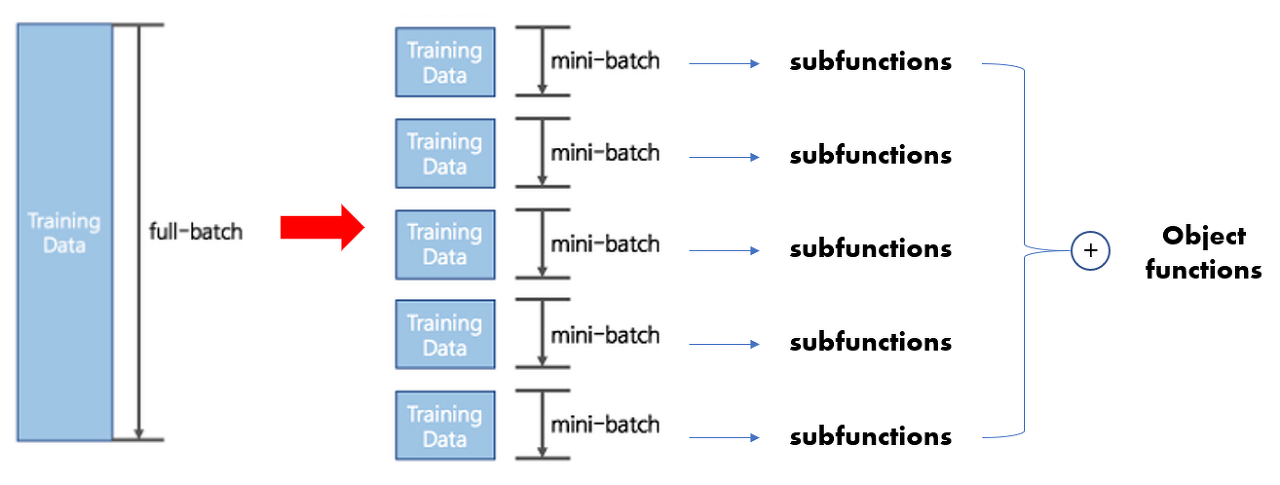
-
많은 object function은 각각의 mini-batch로 분할된 Training Data에서 계산된 subfunctions의 합으로 구성
-
이러한 경우 mini-batch마다 gradient steps(학습으로 수정하는 gradient의 방향, 크기)을 다르게 줄 수 있기 때문에, 학습에 효율적임 -> SGD가 이에 해당(SGD의 경우 데이터 하나마다의 gradient 방향, 크기를 고려하는 것이 가능)
-
하지만, object function에는 noise가 발생하면 optimization의 성능이 저하됨
▶ 대표적인 nosie로 dropout regularization이 있음
▶ object function에 noise가 생긴다면, 더 효율적인 stochastic optimization이 요구됨
- 본문에서는 higher-order optimization method 보다는 first-order methods로 이러한 문제를 해결하고자 함
🟡 기존 SGD의 대체안, ADAM

- Adam은 first-order gradient를 필요로하기에, 메모리 필요량이 적음
- Adam은 gradient의 첫번째와 두번째의 moment estimate로 다른 파라미터에 대한 개별적인 learing rate(학습률)을 계산
- 첫번째 moment의 추청지 : momentum optimizer
- 두번째 moment의 추정치 : AdaGrad / RMSProp optimizer - Adam은 AdaGrad의 장점(sparse gradient에서 잘 작동)과 PMSProp의 장점(온라인과 고정되지 않은 세팅에 잘 작동)을 결합
- 매개변수 업데이트의 크기가 그라디언트의 크기 조정에 변하지 않음
- step size가 대략 step size hyper parameter에 의해 제한되며, 고정 매개변수가 필요하지 않음
- sparse gradient에 작동
- 자연스럽게 step size annealing(step size에 따라 값을 풀어주는것??) 수행

위의 그림이 바로 논문에서 제시하는 Adam Optimizer의 pseudo 코드다.
실제로 moment 2개로 이뤄졌으면서, bias-corrected value를 최종 gradient 산출에 사용한다는 점도 꼭 보고 넘어가야한다.
5. RELATED WORK

논문에서는 RMSProp, AdaGrad의 장점을 잘 융합해서 Adam을 만들었다고 하였고, 실제로 RMSProp과 AdaGrad에 대해서 related work 에 정리해두었다
🏷️ AdaGrad

- gradient의 업데이트 횟수에 따라 학습률(Learning rate)를 조절하는 옵션이 추가된 최적화 방법
- ⨀ : 행렬의 원소별 곱셈
- h는 기존 기울기 값을 제곱하여 계속 더해주고, parameter W를 갱신할 때는 1/√h 를 곱해서 학습률을 조정함
- parameter 중에서 크게 갱신된(gradient가 큰) parameter는, 즉 가 큰 parameter는 h 값이 크게 증가하고 가 감소하면서 학습률이 감소한다고 볼 수 있다
- 즉 gradient가 크면 오히려 learning rate(step size)는 작아지고, gradient가 작으면 learning rate(step size)가 커진다
- AdaGrad는 개별 매개변수에 맞춤형 값을 만들어준다
- 같은 입력 데이터가 여러번 학습되는 학습모델에 유용하게 쓰이는데 대표적으로 언어와 관련된 word2vec이나 GloVe에 유용하다. 이는 학습 단어의 등장 확률에 따라 변수의 사용 비율이 확연하게 차이나기 때문에 많이 등장한 단어는 가중치를 적게 수정하고 적게 등장한 단어는 많이 수정할 수 있기 때문
AdaGrad python 구현
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
# 0으로 나누는 일이 없도록 1e-7을 더해줍니다. 이 값은 임의로 지정 가능합니다.🏷️ RMSProp
- AdaGrad는 과거의 기울기를 제곱하여 계속 더해가기 때문에 학습을 진행할수록 갱신 강도가 약해진다. 무한히 계속 학습할 경우에는 어느 순간 갱신량이 0이 되어 전혀 갱신되지 않게 된다.
- 이 문제를 개선한 기법이 RMSProp!
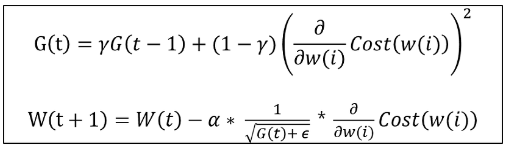
- RMSProp는 과거의 모든 기울기를 균일하게 더하지 않고 먼 과거의 기울기는 서서히 잊고 새로운 기울기 정보를 크게 반영 -> decaying factor(decaying rate)라는 인자 사용
- 지수이동평균 (Exponential Moving Average, EMA)를 사용해 이를 구현하는데, 과거 기울기의 반영 규모를 기하급수적으로 감소시킴
RMSProp python 구현
class RMSprop:
def __init__(self, lr=0.01, decay_rate = 0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)🏷️ Momentum
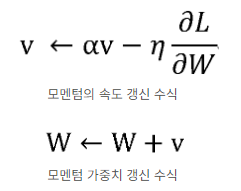
- W : 갱신할 가중치 매개변수
- L : 손실함수(loss function)
- η : 학습률 (learning rate),
- : W 에 대한 손실함수의 기울기
- 변수 v ??
: 물리에서 운동량을 나타내는 식은 p = mv, 질량 m, 속도 v
=> 위 수식에서도 v는 속도
=> 매개변수 α를 v에 곱해서 αv 항은 물체가 아무 힘도 받지 않을 때도 서서히 하강시키는 역할
=> gradient의 방향이 변경되어도 이전 방향과 크기에 영향받아 다른 방향으로 가중치가 변경될 수 있음
Momentum python 구현
import numpy as np
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr #η
self.momentum = momentum #α
self.v = None
def update(self, params, grads):
# update()가 처음 호출될 때 v에 매개변수와 같은 구조의 데이터를 딕셔너리 변수로 저장
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]2. ALGORITHM
◻️ Adam Pseudo code

위의 수식에 대해서 조금씩 뜯어서 보기로 한다.
함수 속 인자에 대한 설명은 위의 정의를 참고한다.
사실상 hyper parameter라 할 것들이,
(Step size), (첫번째 moment 추정치를 얼마나 버릴지), (두번째 moment 추정치를 얼마나 버릴지) 결정하는 것들 밖에 없다. (도 있음)
adam은 크게 moment를 계산하는 부분, moment를 bias로 조정하는 부분으로 구성됨
moment는 Momentum이 적용된 first moment와 AdaGrad, RMSProp이 적용된 second moment가 있음
◻️ 초기에 설정해야하는 4가지 파라미터(Require)
- Stepsize (Learing Rate)
- Decay Rates
: Exponential decay rates for the moment estimates (0~1 사이의 값)
-> Adam의 유일한 hyper-parameter, gradient의 decay rate를 조절함 - Stochastic Objective Function f(θ) - loss function
-> ( θ (parameters, weight 값) 주어질 때-> f(θ) 값의 최소화가 adam의 목표 ) - initial Parameter Vector
◻️ Adam optimizer 수행 과정
(1) first & Second moment, time step 초기화
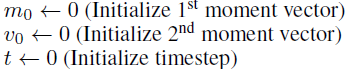
(2) 파라미터 θ_t가 수렴(converge)할 때까지 반복

(반복문-1) time step 증가 : t <- t+1
- iteration 별로 값들이 계속 업데이트 됨.
(반복문-2) stochastic objective funtion으로 이전 time step의 gradient 계산 (미분)
- stochastic objective function(loss function)을 통해 나온 값을 바탕으로 weight별 gradient 계산 (1차 미분, first-order gradient)
(반복문-3) biased first & second moment 값 계산
- : Momentum 해당 -> fisrt moment
- : AdaGrad, RMSProp 에 해당 -> second moment
- 가 최신 값의 비중을 조절하는 역할 (exponential decay)
(반복문-4) 초기의 모멘텀 값이 0으로 초기화되는 경우를 방지하기 위해, bias-correction 적용
- : 을 (1-) 로 나누어서 bias-correction 수행
- : 을 (1-) 로 나누어서 bias-correction 수행
- 초기의 모멘텀 값이 0으로 초기화되는 경우를 방지하기 위해, bias-correction 적용
(반복문-5) 최종 파라미터(가중치) 업데이트
- 은 0으로 나누는 일을 방지하기 위해 셋팅
- second moment가 AdaGrad, RMSProp 역할 -> 파라미터의 업데이트 횟수에 따라 학습률을 달리 함
- 업데이트를 많이 한 파라미터일수록 값이 커짐 -> 전체적으로는 파라미터 업데이트 많이 했을수록 step size를 줄여주는 효과
학습률 조절 방법
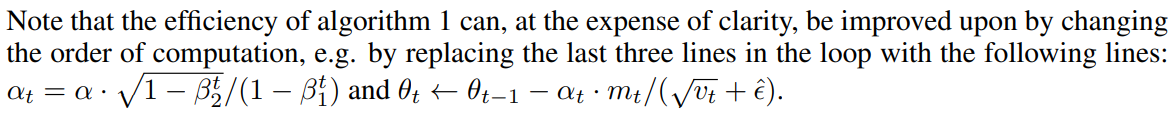
- 고정값으로 설정하는 도 이렇게 iteration 마다 와 을 사용해 변화를 줄 수 있다.
- 성능적인 면에서 효과 볼 수 있음
◻️ ADAM’S UPDATE RULE
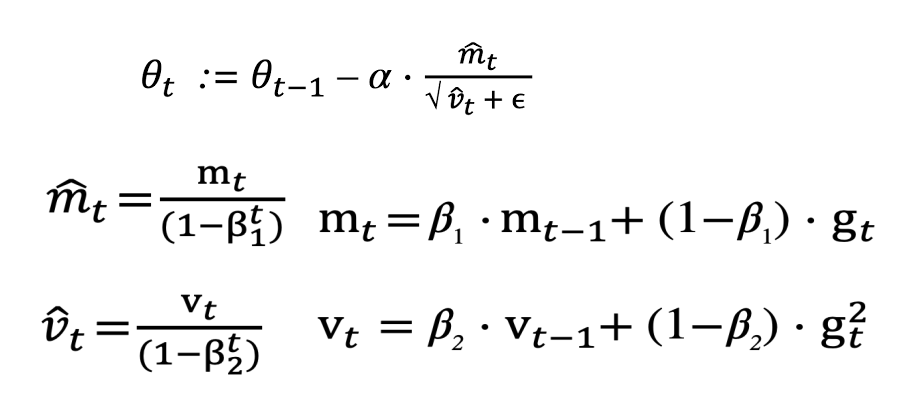
위의 식이 Adam의 파라미터 Update 식이다.
- Adam의 핵심은 step size(Learning Rate)를 효과적으로 선택하는 것!
- 효과적인 step size은 의 값을 최적으로 만듬
- step size는 2개의 upper bounds(상한선)이 있음 (if, = 0 )

-
First case는 sparsity case 일때 적용 (sparsity case : 하나의 gradient가 모든 time step에서 0으로 되는 경우)
=> 이럴때는 step size를 크게 해서 업데이트 변화량을 크게 만들어야함
=> (1-) >
=> 학습률이 커짐 -
Second case는 일반적인 경우 (대부분 = 0.9, = 0.99으로 설정)
=> (1-) <=
=> 이럴때는 step size를 작게 해서 업데이트 변화량을 작게 만듦
=> 학습률이 작아짐
3. INITIALIZATION BIAS CORRECTION
위에 수식에서 의문이 들 수 있다.
도대체 왜, 각 모멘트를 1- 로 나누는가...?🤔🤔
- : 을 (1-) 로 나누어서 bias-correction 수행
- : 을 (1-) 로 나누어서 bias-correction 수행
일단 논문에서는 second moment 에 대해서 로 추정하는 이유를 설명했다.
이 과정을 진행하나 의문이 들수 있는데 그 이유가 여기 있다.
직접 수식으로 풀어서 정리해보자면,

그리고
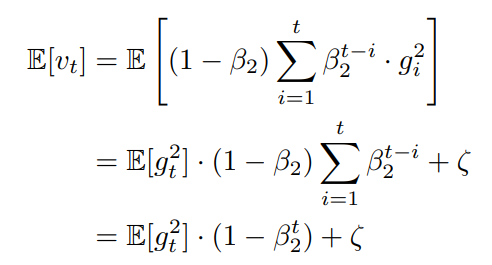
= 0 이라면,
실제로 구해야하는 참 second momet 기댓값 이 되고,
가 에 근사하기 위해, 를 나누게 됨
sparse gradient의 경우, 값을 작게 설정함 -> 이전 time step의 기울기를 최대한 무시하게 됨
4. CONVERGENCE ANALYSIS

=> 결론적으로는 comverge 함
6. EXPERIMENTS
6.1 EXPERIMENT: LOGISTIC REGRESSION
[평가 데이터셋 1 : MNIST 데이터셋]
- multi-class logistic regression (L2-regularized 적용)
- step size α는 1/√t decay로 조정됨 -> 시간에 따라 step size 감소
- logistic regression를 사용해 784 차원의 이미지 벡터로 숫자 class를 분류
- mini batch 128로 Adam, SGD(with Nesterov), AdaGrad를 비교 (아래 표 1의 왼쪽 그래프)
- 표1을 보면, adam은 SGD와 유사하게 수렴하고, AdaGrad 보다 빠르게 수렴하는 것을 볼 수 있음
[평가 데이터셋 2 : IMDB 데이터셋]
- sparse feature problme을 테스트 하기 위해 IMDB 영화 리뷰 데이터셋으로도 adam을 평가함
- sparse feature problem : 비슷한 유형이 적은 데이터(unique value 가 많은 데이터)
- BoW(Bag of Words) Features vector로 전처리 진행 (10,000 차원)
- Bow Feature Vector : 문장을 벡터(숫자)로 표현
- 오버피팅을 방지하기 위해 50% 비율의 drop-out이 적용되며, 이 노이즈가 BoW Features에 적용됨
- 위 표 1의 오른쪽 그래프를 보면 loss 값이 상당히 튀는 것을 볼 수 있는데, 이것이 drop-out의 noise
- sparse한 경우 Adam, RMSProp, Adagrad는 좋은 성능을 내고 있음 (표 1의 오른쪽 그래프)
Adam은 sparse features에서도 성능이 좋으며, SGD보다 빠른 수렴 속도를 지니고 있음

- x축 : 학습 횟수, y축 : loss 값
6.2 EXPERIMENT: MULTI-LAYER NEURAL NETWORKS
- MINST 데이터셋 사용
- multi-layer model : two fully connected hidden layer with 1000 hiden units (ReLU activation, mini-batch 128)
- Object Function : Cross-Entropy Loss (with L2 weight decay)
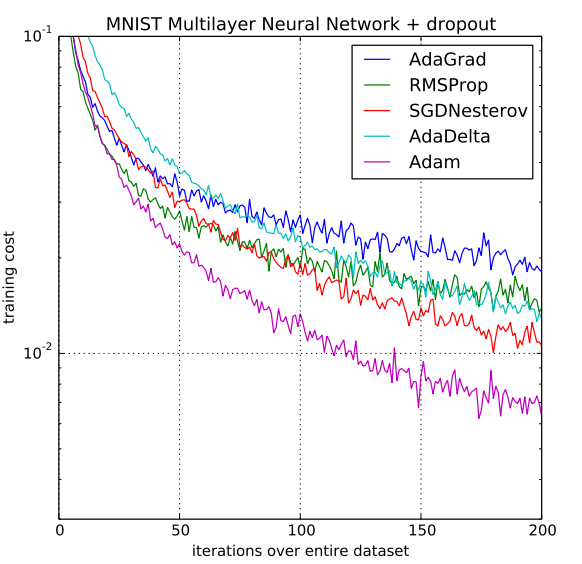
- x축 : 학습 횟수, y축 : loss 값
- drop-out regularization을 적용했을 때의 optimizer 성능 비교 -> Adam이 가장 빠르게 수렴
6.3 EXPERIMENT: CONVOLUTIONAL NEURAL NETWORKS
[평가 데이터셋 3 : CIFAR-10 데이터셋]
- Convolution Neural Network : C64-C64-C128-1000
- C64 : 64 output channel을 가지는 3*3 conv layer
- 1000 : 1000 output을 가지는 dense layer
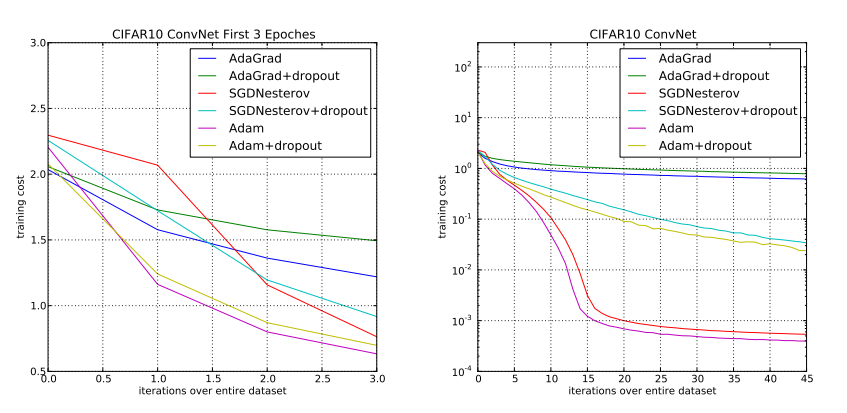
- 왼쪽 그래프 : 3 epoch 까지의 optimizer 별 수렴 속도 비교
- 오른쪽 그래프 : 45 epoch 까지의 optimizer 별 수렴 속도 비교
- x축 : 학습 횟수, y축 : loss 값
- dropout을 적용하지 않은 optimizer 중에서 Adam이 제일 수렴 속도가 빠름
- dropout을 적용한 optimizer 중에서 Adam이 제일 수렴 속도가 빠름
6.4 EXPERIMENT: BIAS-CORRECTION TERM
- Stepsize α, Decay Rates B1, B2에 따른 Training Loss 그래프
- x축 : log(step_size), y축 : Loss
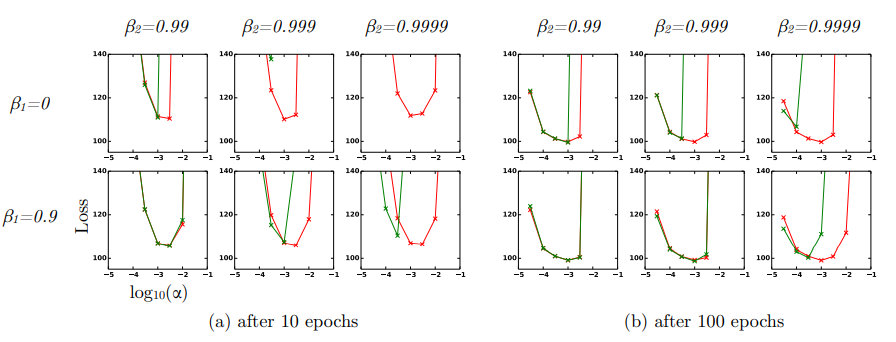
- 초록색 그래프 : no bias correction terms -> RMSProp
- 빨간색 그래프 : bias correction terms (1-B)
- Bias correction term을 적용하지 않았을 때 B2가 1.0에 가까워질수록 불안정
=> 요약하자면 Adam 알고리즘은 하이퍼파라미터 설정에 상관없이 RMSProp 이상의 성능을 보였다.
7. EXTENSION
ADAMAX
Adam에서 개별 weights를 업데이트 하기 위해 과거와 현재의 gradient의 L2 norm을 취함
이때 L2 norm을 L_p norm으로 변경할 수 있음
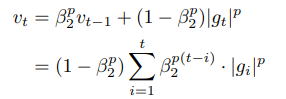
=> p 값이 커질수록 수치적으로 불안정해지나, p를 무한대라고 가정(infinity norm)하면 간단하고 stable한 알고리즘이 됨

TEMPORAL AVERAGING
마지막 반복은 확률적 근사로 인해 잡음이 많기 때문에 파라미터 평균화를 통해 더 나은 일반화 성능을 얻을 수 있는 경우가 많다.
8. CONCLUSION
- Stochastic objective function의 최적화를 위해 간단하고 효율적인 최적화 알고리즘 Adam을 소개함
- 대량의 데이터셋과 고차원의 파라미터 공간에 대한 머신러닝의 문제 해결에 집중
- Adam은 AdaGrad가 Sparse gradients를 다루는 방식(파라미터 별 step size를 다르게 적용)과 RMSProp이 non-stationary(정지하지 않는) objectives를 다루는 방식(과거의 기울기를 현재의 것보다 덜 반영함)을 조합
- Adam은 non-convex한 문제(여러 개의 최저점이 있는 문제)에서도 최적화가 잘 됨
🔖 Reference
논문 리류 포스팅 참고
AdaGrad, RMSProp 이론
Optimizer 총정리(코드포함)
Adam 논문 리뷰 영상
Optimizer 수식 정리
