[딥러닝] 순방향 연산 및 역전파 / 크로스엔트로피

황성미·2023년 10월 31일

DL DeepLearning 딥러닝 제로베이스 제로베이스데이터스쿨 제로베이스스쿨 파이썬

제로베이스 데이터스쿨

목록 보기

49/58

✍🏻 31일 공부 이야기.

오늘 공부한 실습 코드는 위 깃허브 사진을 클릭하면 이동합니다 :)

본격적으로 오늘 배울 내용을 정리하기 전, 간단하게 딥러닝에 대한 인사이트(?) 몇 개만 보고 가시죵

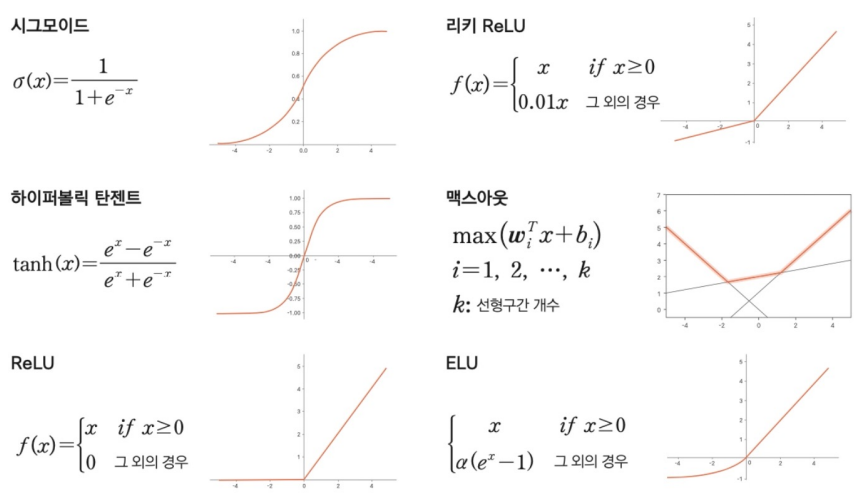
📌 지난 블로그에서 정리했던 활성화 함수의 종류 총 정리

📌 규모에 따른 딥러닝 모델 종류 정리

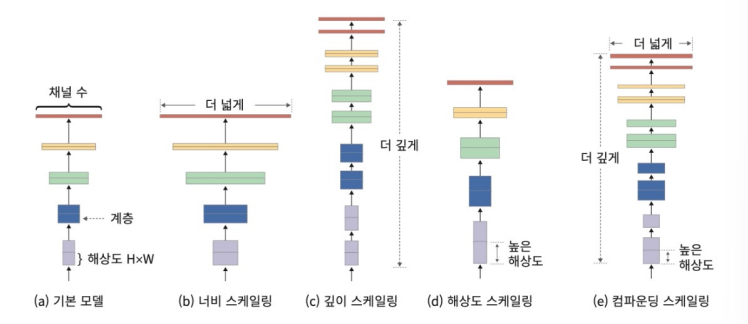
Deep Learning from scratch

순방향 연산

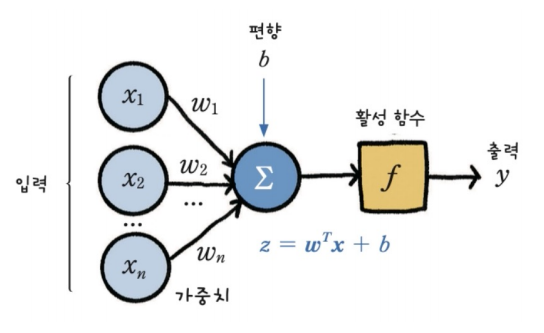
왼쪽에서 오른쪽의 방향으로 가는, 입력에서 가중치와 편향을 주고 활성 함수를 통과시켜 출력값을 얻는 과정을 <순방향 연산>이라고 한다.

흐름만 살짝 살펴보자면 아래와 같다.

📌 데이터 준비

import numpy as np

X = np.array([
    [0,0,1], 
    [0,1,1],
    [1,0,1],
    [1,1,1]
])

📌 활성화 함수

# 활성화 함수 sigmoid
def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))

📌 순방향 연산(출력값 얻어내기)

W = 2 * np.random.random((1, 3)) -1 # 랜덤하게 선택된 가중치


# 추론(순방향 연산)
N = 4

for k in range(N):
    x = X[k, :].T 
    v = np.matmul(W, x)
    y = sigmoid(v)

    print(y)

💻 출력

[0.30389718][0.33752218]
[0.53475609][0.57290196]

위 과정처럼 데이터에 가중치와 편향을 주고 활성화함수를 거쳐 출력값을 얻는 흐름을 순방향 연산이라고 한다.

지금은 가중치를 랜덤하게 선택하게 하고 음수에서부터 양수까지 다양한 값을 가지게 하기 위해 2를 곱하고 1을 빼주는 작업을 실시해주었는데,
실제로는 학습된 가중치를 주어야한다.

그렇다면 학습된 가중치는 어떻게 찾아낼 수 있을까?

학습 원리

먼저 학습을 위해선 정답지가 필요하다.

정답지를 주고 학습된 가중치를 얻어보자.

# 정답지
D = np.array([
    [0], [0], [1], [1]
])

우리는 이제 정답지도 있으니, 출력값과 정답지와의 오차를 구해 그 오차가 작아지도록 하는 가중치를 구하면 된다.

# 출력값 계산
def calc_output(W, x):
    v = np.matmul(W, x)
    y = sigmoid(v)
    return y

# 오차 계산
def calc_error(d, y_pred):
    e = d - y_pred
    delta = y_pred * (1 - y_pred) * e
    return delta

반복되는 출력값과 오차의 계산을 함수로 표현해 간단하게 만들어 주었다.

그런데 calc_error함수에 있는 e는 출력값과 실제값의 차이이지만 delta는 어떻게 나온 식일까?

이를 알기 위해선 시그모이드 함수를 다시 살펴볼 필요가 있다.

# 시그모이드 함수의 미분 형태
import sympy as sym

z = sym.Symbol('z')
s = 1 / (1 + sym.exp(-z)) # 시그모이드 함수 형태
sym.diff(s) # 시그모이드 함수 미분 형태

💻 출력

$(1 + e^{−z}) \over(1 + e^{−z})^2$

파이썬의 sympy를 이용하면 위와 같이 미분식을 쉽게 얻어낼 수 있다.

위 사진의 화살표 부분의 식이 도출이 된 것이고
이 식을 좀 더 전개해나아가다 보면 하이라이트 된 식과 같이 시그모이드 값으로 변환시킬 수 있다.

그래서 delta값의 y_pred * (1 - y_pred) * e 의 y_pred * (1 - y_pred)부분은 e의 미분값임을 알 수 있고
오차를 뒤로 전해줄 때 단순히 차이만 계산하는 것이 아닌 미분값을 같이 곱해서 넘겨주는 것이다.

미분값을 같이 곱해주는 이유는 위와 같은데, 아마 <역전파>파트에서 더 자세히 다룰 예정이다.

📌 Gradient Descent를 이용한 W 업데이트 식

# 한 epoch에 수행되는 W 계산(gradient descent)
def delta_GD(W, X, D, alpha):
    # 모든 데이터에 대해 계산하는 gradient descent 방식에 따라
    # 전체 데이터 개수인 4개를 다 거쳐야함
    for k in range(4):
        x = X[k, :].T # 입력값
        d = D[k] # 실제값(정답지)

        y_pred = calc_output(W, x) # 순방향 추론
        delta = calc_error(d , y_pred) # delta 계산

        dW = alpha * delta * x # 가중치 변화량
        W = W + dW # 가중치 업데이트
    return W

alpha = 0.9
for epoch in range(1000):
    W = delta_GD(W, X, D, alpha)
    print(W)

이렇게 계산된 함수를 이용해 기존 랜덤하게 선택된 가중치를 학습을 통해 업데이트 시켜나가면 array([[ 7.15327831, -0.22405033, -3.35616859]])라는 최종 값을 얻게 되고

calc_output(W, X.T)

💻 출력

array([[0.03369375, 0.02711394, 0.97805678, 0.97269656]])

위 식을 통해 학습된 가중치로 얻어낸 예측값도 확인할 수 있다.

초반 랜덤으로 선택된 가중치로 얻어낸

[0.30389718][0.33752218]
[0.53475609][0.57290196]

값과는 달리 정답지(0,0,1,1)에 근사한 값이 나온 것을 볼 수 있다.

역전파

역전파에 대해... 대학 시절 수학적인 이론부터 배운 사람으로서(??) 다시 그 기억을 끄집어내어 정리하고, 블로그에도 올리고 싶었지만 강의 양이 너무 많아서 할 수가 없었다 😭

Instagram에서 이 게시물 보기

데이터분석가 황성미(@castle._.mi_data)님의 공유 게시물

지금은 공스타그램에 업로드해둔 링크를 첨부해두고 역전파에 대해서는 꼭 다시 정리해둬야지...!!

이전 블로그에서 실습했던 XOR문제를 다시 실습해보자.

# 데이터 준비
import numpy as np

X = np.array([[0,0,1],
              [0,1,1],
              [1,0,1],
              [1,1,1]])
D = np.array([[0], [1], [1], [0]])

W = 2 * np.random.random((1, 3)) -1


# 학습을 통한 가중치 업데이트
alpha = 0.9
for epoch in range(1000):
    W = delta_GD(W, X, D, alpha)
    
    
# 학습된 결과를 통해 예측된 값
calc_output(W, X.T)

💻 출력

array([[0.52965337, 0.5 , 0.47034663, 0.44090112]])

위에서 사용했던 함수들을 사용해서 예측해보았는데 생각보다 잘 된 것같진 않다.

레이어를 한 단계 더 쌓고 역전파를 이용해 다시 예측해보자.

레이어를 쌓을 때는 항상 계산되는 shape을 신경써서 코드를 짜주어야한다.

나는 강의 코드를 따라 쳤음에도 자꾸 에러가 떠서.. 일일이 다 shape도 확인해보고 어디를 수정해줘야하는지 찾아보고 그랬다... 🫥🤯 이거시 딥러닝이지....
(딥러닝의 세계에 온 것을 환영한다는걸 알리는 듯... ㅎㅎ)

def calc_output(W1, W2, x):
    # W1 (4, 3) 
    # x = X[k, :].T (3, )
    v1 = np.matmul(W1, x)
    y1 = sigmoid(v1) # (4, )
    # W2 (1, 4)
    v = np.matmul(W2, y1)
    y = sigmoid(v) # (1, )

    # print('y : ', y.shape) # (1, )
    # print('y1 : ', y1.shape) # (4, )
    return y, y1

# 출력층 델타 계산
def calc_delta(d, y):
    e = d - y
    delta = y*(1-y)*e
    # print('delta : ', delta.shape) # (1, )
    return delta

# 은닉층 델타 계산
def calc_delta1(W2, delta, y1):
    e1 = np.matmul(W2.T, delta)
    delta1 = y1*(1-y1)*e1
    # print('delta1 : ', delta1.shape) # (4,)
    return delta1

# 역전파를 이용한 가중치 업데이트 계산 함수
def backprop_XOR(W1, W2, X, D, alpha):
    for k in range(4):
        x = X[k, :].T #(3, )
        d = D[k]

        y, y1 = calc_output(W1, W2, x)
        delta = calc_delta(d, y)
        delta1 = calc_delta1(W2, delta, y1)

        # alpha : 상수 /  delta1 : (4 , ) / x : (3 , )
        dW1 = (alpha * delta1).reshape(4, 1) * x.reshape(1, 3)
        W1 = W1 + dW1

        # alpha : 상수 /  delta : (1 , ) / y1 : (4, )
        dW2 = alpha * delta * y1
        W2 = W2 + dW2

    return W1, W2

레이어를 하나 더 쌓아준 다음 출력층과 은닉층의 델타를 계산하고 계산된 델타를 통해 가중치를 업데이트하는 함수를 작성했다.

이들을 이용해 다시 가중치를 랜덤하게 초기화하고 다시 학습시켜보면 아래와 같다.

X = np.array([[0,0,1],
              [0,1,1],
              [1,0,1],
              [1,1,1]])
D = np.array([[0], [1], [1], [0]])

W1 = 2 * np.random.random((4, 3)) -1 # 첫번째 가중치
W2 = 2 * np.random.random((1, 4)) -1 # 두번째 가중치


# 학습
alpha = 0.9
for epoch in range(10000):
    W1, W2 = backprop_XOR(W1, W2, X, D, alpha)
    
# 예측 결과    
for k in range(4):
    x = X[k, :].T
    y, y1 = calc_output(W1, W2, x)
    print(y)

💻 출력

[0.006909][0.99022793]
[0.9896984][0.01419835]

실제값인 0,1,1,0과 유사한 값을 보이는 것을 확인할 수 있다.

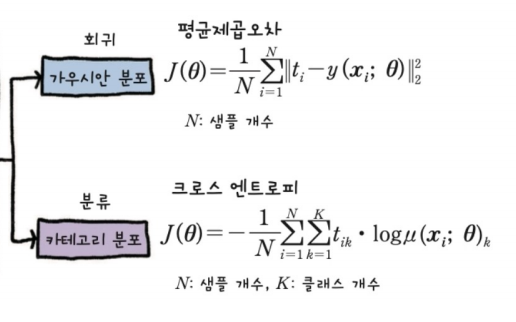
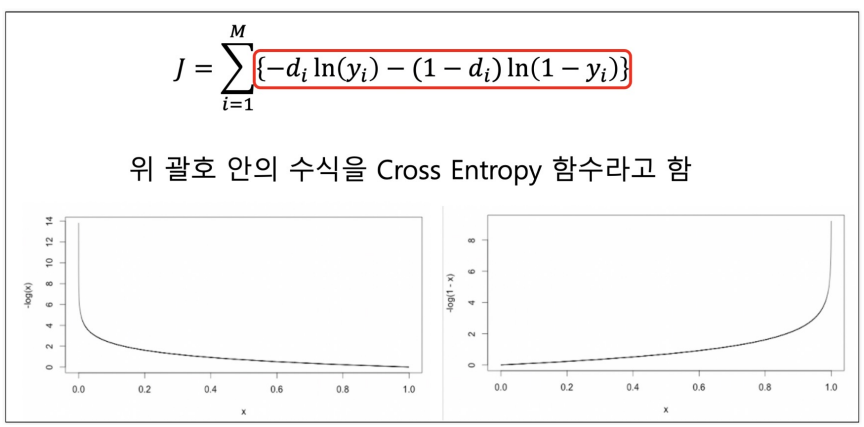
크로스엔트로피

그동안 loss함수를 mse로 많이 사용해왔다.

이번에는 다른 종류의 loss 함수 중 크로스 엔트로피에 대해 알아보고 이를 이용한 가중치 업데이트도 실습해보자.

크로스엔트로피는 분류 문제에서 흔히 사용되며 U자의 형태를 띄고 있다.

함수를 만들기 위해서는 앞에서 했던 것처럼 미분식을 알아야한다.

크로스 엔트로피 함수의 미분식에 대해 정리된 글을 찾다가 위 글을 발견했다.

위의 수식을 따라가다보면 우리는 크로스 엔트로피 함수의 미분식은 결국 예측값 - 실제값이라는 사실을 알 수 있다.

그러므로 아래와 같이 함수를 만들 수 있고 그 결과까지 한 번 살펴봐보자.

📌 cross-entropy를 이용한 함수

# cross entropy의 출력층 델타
def calc_crossentropy_delta(d, y):
    # d : 실제값, y : 예측값
    e = d - y
    delta = e
    return delta

# cross entropy의 은닉층 델타 
def calc_crossentropy_delta1(W2, delta, y1):
    e1 = np.matmul(W2.T, delta)
    delta1 = y1*(1-y1)*e1
    return delta1

# 역전파를 이용한 가중치 업데이트 계산 함수
def backprop_CE(W1, W2, X, D, alpha):
    for k in range(4):
        x = X[k, :].T 
        d = D[k]

        y, y1 = calc_output(W1, W2, x)
        delta = calc_crossentropy_delta(d, y)
        delta1 = calc_crossentropy_delta1(W2, delta, y1)

        dW1 = (alpha * delta1).reshape(4, 1) * x.reshape(1, 3)
        W1 = W1 + dW1

        dW2 = alpha * delta * y1
        W2 = W2 + dW2

    return W1, W2

📌 결과 확인

W1 = 2 * np.random.random((4, 3)) -1 # 첫번째 가중치
W2 = 2 * np.random.random((1, 4)) -1 # 두번째 가중치

# 학습
alpha = 0.9
for epoch in range(10000):
    W1, W2 = backprop_CE(W1, W2, X, D, alpha)

# 결과
for k in range(4):
    x = X[k, :].T
    y, y1 = calc_output(W1, W2, x)
    print(y)

💻 출력

[8.49056272e-05][0.99990643]
[0.99990171][0.00019382]

이 또한 적절하게 예측값이 나온다 😊😊

예제

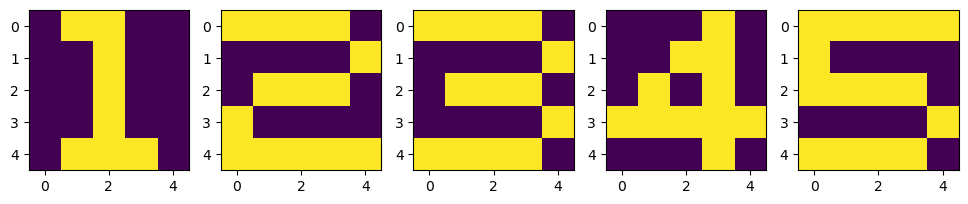
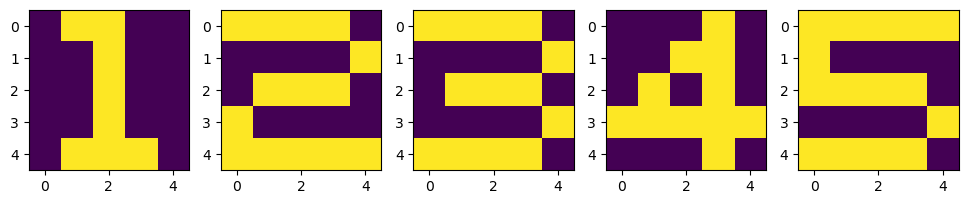
이번에는 위와 같이 하나의 칸을 색깔로 채워 숫자를 만든 다음 해당 숫자를 잘 인식할 수 있는 모델을 만들어보자.

미리 결론부터 말하자면... 내가 했을 때엔 예측값이 거의 다 틀렸다 ㅎㅎ

alpha와 epoch 값도 달리해가며 여러 번 돌려봤는데 제대로 학습이 안 되었나부다.. ㅠ

그래도 정리는 해야하니깐~!!!!ㅋㅋㅋㅋ

📌 데이터 준비

X = np.zeros((5, 5, 5))

X[:, :, 0] = [[0,1,1,0,0], [0,0,1,0,0], [0,0,1,0,0], [0,0,1,0,0], [0,1,1,1,0]]
X[:, :, 1] = [[1,1,1,1,0], [0,0,0,0,1], [0,1,1,1,0], [1,0,0,0,0], [1,1,1,1,1]]
X[:, :, 2] = [[1,1,1,1,0], [0,0,0,0,1], [0,1,1,1,0], [0,0,0,0,1], [1,1,1,1,0]]
X[:, :, 3] = [[0,0,0,1,0], [0,0,1,1,0], [0,1,0,1,0], [1,1,1,1,1], [0,0,0,1,0]]
X[:, :, 4] = [[1,1,1,1,1], [1,0,0,0,0], [1,1,1,1,0], [0,0,0,0,1], [1,1,1,1,0]]

# 정답지
D = np.array([[[1,0,0,0,0]], [[0,1,0,0,0]], [[0,0,1,0,0]], [[0,0,0,1,0]], [[0,0,0,0,1]]])

plt.figure(figsize=(12, 4))
for n in range(5):
    plt.subplot(1, 5, n+1)
    plt.imshow(X[:, :, n])
plt.show()

💻 출력

위와 같이 코드를 짜면 아까 초반에 보았던 그림으로 그린 1, 2, 3, 4, 5가 만들어진다.

우리는 이 숫자들을 RELU 3번, Softmax 1번을 거친 모델로 학습시켜 볼 것이다.

📌 ReLU와 Softmax 함수 계산 및 순방향 계산 함수

# softmax
def softmax(x):
    # subtract : 두 값의 차이 계산
    # 최대값과의 차이를 exp 해줌으로써 일종의 min-max scaler를 적용해 overflow를 막아준 셈
    x = np.subtract(x, np.max(x)) 
    ex = np.exp(x)

    return ex / np.sum(ex)
    
# relu : 음수는 모두 0으로 이외의 값은 해당 값으로 반환해줌
def ReLU(x):
    # np.maximum : 여러 array 사이에서 각 위치의 최대값 반환
    return np.maximum(0, x)


# 순방향 계산
def calc_output_relu(W1, W2, W3, W4, x):
    v1 = np.matmul(W1, x)
    y1 = ReLU(v1)
    v2 = np.matmul(W2, y1)
    y2 = ReLU(v2)
    v3 = np.matmul(W3, y2)
    y3 = ReLU(v3)
    v = np.matmul(W4, y3)
    y = softmax(v)

    return y, v1, v2, v3, y1, y2, y3

📌 델타 계산 및 가중치 업데이트 계산 함수

# 역전파를 이용한 델타 계산
def backprop_ReLU(d, y, W2, W3, W4, v1, v2, v3):
    e = d - y
    delta = e

    e3 = np.matmul(W4.T, delta)
    delta3 = (v3 > 0)*e3

    e2 = np.matmul(W3.T, delta3)
    delta2 = (v2 > 0)*e2

    e1 = np.matmul(W2.T, delta2)
    delta1 = (v1 > 0)*e1

    return delta, delta1, delta2, delta3


# 델타를 이용한 가중치 업데이트 계산
def calc_Ws(alpha, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4):
    dW4 = alpha*delta*y3.T
    W4 = W4 + dW4

    dW3 = alpha*delta3*y2.T
    W3 = W3 + dW3

    dW2 = alpha*delta2*y1.T
    W2 = W2 + dW2

    dW1 = alpha*delta1*x.T
    W1 = W1 + dW1

    return W1, W2, W3, W4
    
    
# 가중치 업데이트
def DeepReLU(W1, W2, W3, W4, X, D, alpha):
    for k in range(5):
        x = np.reshape(X[:, :, k], (25, 1))
        d =D[k, :].T
        
        y, v1, v2, v3, y1, y2, y3 = calc_output_relu(W1, W2, W3, W4, x)
        delta, delta1, delta2, delta3 = backprop_ReLU(d, y, W2, W3, W4, v1, v2, v3)
        W1, W2, W3, W4 = calc_Ws(alpha, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4)

        return W1, W2, W3, W4

📌 학습 및 검정 결과

# 학습
W1 = 2*np.random.random((20, 25)) -1
W2 = 2*np.random.random((20, 20)) - 1
W3 = 2*np.random.random((20, 20)) - 1
W4 = 2*np.random.random((5, 20)) - 1

alpha = 0.001
for epoch in tqdm_notebook(range(10000)):
    W1, W2, W3, W4 = DeepReLU(W1, W2, W3, W4, X, D, alpha)
    
    
# 검증
def verify_algorithm(x, W1, W2, W3, W4):
    v1 = np.matmul(W1, x)
    y1 = ReLU(v1)

    v2 = np.matmul(W2, y1)
    y2 = ReLU(v2)

    v3 = np.matmul(W3, y2)
    y3 = ReLU(v3)

    v = np.matmul(W4, y3)
    y = softmax(v)

    return y
    
# 결과
N= 5
for k in range(N):
    x = np.reshape(X[:, :, k], (25, 1))
    y = verify_algorithm(x, W1, W2, W3, W4)
    print("Y = {} : ".format(k+1)) # 실제값
    print(np.argmax(y, axis=0)+1)  # 예측값 
    print(y)
    print('--------------------')

📌 테스트 데이터에 대한 예측 및 결과

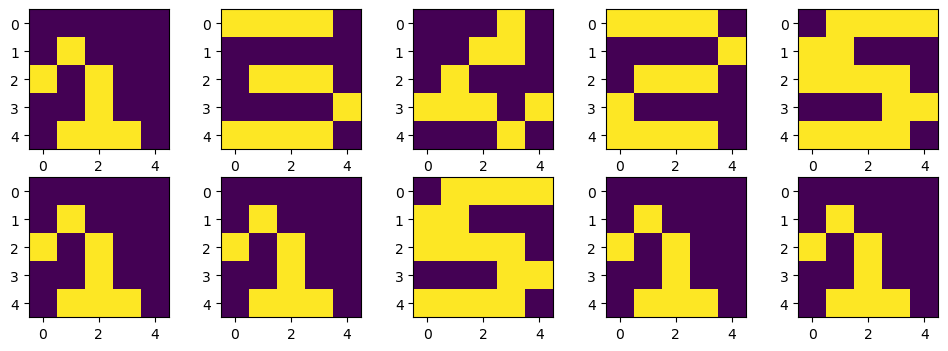
# 테스트
X_test = np.zeros((5, 5, 5))

X_test[:, :, 0] = [[0,0,0,0,0], [0,1,0,0,0], [1,0,1,0,0], [0,0,1,0,0], [0,1,1,1,0]]
X_test[:, :, 1] = [[1,1,1,1,0], [0,0,0,0,0], [0,1,1,1,0], [0,0,0,0,1], [1,1,1,1,0]]
X_test[:, :, 2] = [[0,0,0,1,0], [0,0,1,1,0], [0,1,0,0,0], [1,1,1,0,1], [0,0,0,1,0]]
X_test[:, :, 3] = [[1,1,1,1,0], [0,0,0,0,1], [0,1,1,1,0], [1,0,0,0,0], [1,1,1,1,0]]
X_test[:, :, 4] = [[0,1,1,1,1], [1,1,0,0,0], [1,1,1,1,0], [0,0,0,1,1], [1,1,1,1,0]]


# 예측
learning_result = [0,0,0,0,0]

for k in range(N):
    x = np.reshape(X_test[:, :, k], (25, 1))
    y = verify_algorithm(x, W1, W2, W3, W4)

    learning_result[k] = np.argmax(y, axis = 0) + 1
    
plt.figure(figsize=(12, 4))
for k in range(5):
    plt.subplot(2, 5, k+1)
    plt.imshow(X_test[:, :, k]) # 원본 데이터

    plt.subplot(2, 5, k+6)
    plt.imshow(X_test[:, :, learning_result[k][0] - 1]) # 예측 데이터
plt.show()

💻 출력

모델이 멍텅구리인가... 1만 맞추고 다 틀렸다 ㅎㅎ

그래서 모델에 융통성을 길러주기 위해 Dropout도 추가해보았다.

DROPOUT

📌 DROPOUT 함수 및 순방향 계산

# dropout 함수
def Dropout(y, ratio):
    ym = np.zeros_like(y) 

    num = round(y.size * (1 - ratio)) 
    # y.size까지의 수 중 num 개수만큼 랜덤으로 추출
    idx = np.random.choice(y.size, num, replace = True)
    ym[idx] = 1.0 / (1.0 - ratio)

    return ym

# dropout 적용시킨 순방향 출력 계산
def calc_output_dropout(W1, W2, W3, W4, x):  
    v1 = np.matmul(W1, x)
    y1 = sigmoid(v1)
    y1 = y1 * Dropout(y1, 0.2)

    v2 = np.matmul(W2, y1)
    y2 = sigmoid(v2)
    y1 = y2 * Dropout(y2, 0.2)

    v3 = np.matmul(W3, y2)
    y3 = sigmoid(v3)
    y3 = y3 * Dropout(y3, 0.2)

    v = np.matmul(W4, y3)
    y = softmax(v)

    return y, y1, y2, y3, v1, v2, v3

📌 델타 계산 및 가중치 업데이트

# 역전파를 이용한 델타 계산
def backprop_dropout(d, y, y1, y2, y3, W2, W3, W4, v1, v2, v3):
    e = d - y
    delta = e

    e3 = np.matmul(W4.T, delta)
    delta3 = y3*(1 - y3)*e3

    e2 = np.matmul(W3.T, delta3)
    delta2 = y2*(1 - y2)*e2

    e1 = np.matmul(W2.T, delta2)
    delta1 = y1*(1 - y1)*e1

    return delta, delta1, delta2, delta3


# 가중치 업데이트
def Deepdropout(W1, W2, W3, W4, X, D):
    for k in range(5):
        x = np.reshape(X[:, :, k], (25, 1))
        d =D[k, :].T
        
        y, y1, y2, y3, v1, v2, v3 = calc_output_dropout(W1, W2, W3, W4, x)
        delta, delta1, delta2, delta3 = backprop_dropout(d, y, y1, y2, y3, W2, W3, W4, v1, v2, v3)
        W1, W2, W3, W4 = calc_Ws(alpha, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4)

        return W1, W2, W3, W4

📌 학습 및 예측

# 학습
W1 = 2*np.random.random((20, 25)) -1
W2 = 2*np.random.random((20, 20)) - 1
W3 = 2*np.random.random((20, 20)) - 1
W4 = 2*np.random.random((5, 20)) - 1

for epoch in tqdm_notebook(range(10000)):
    W1, W2, W3, W4 = Deepdropout(W1, W2, W3, W4, X, D)
    
    
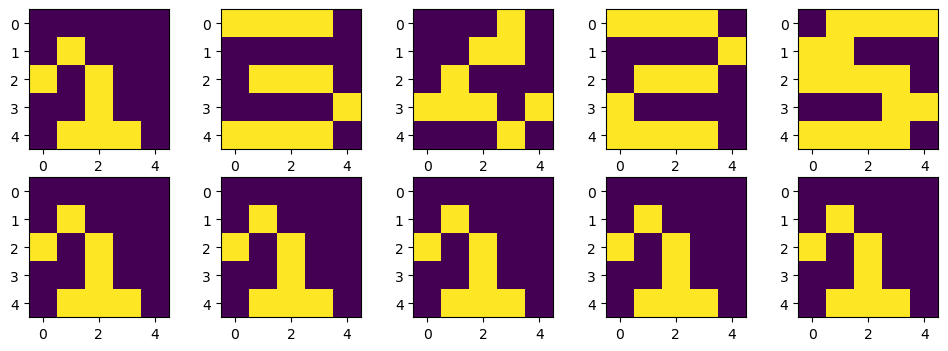
# 테스트 데이터 다시 예측
learning_result = [0,0,0,0,0]

for k in range(N):
    x = np.reshape(X_test[:, :, k], (25, 1))
    y = verify_algorithm(x, W1, W2, W3, W4)

    learning_result[k] = np.argmax(y, axis = 0) + 1
    

plt.figure(figsize=(12, 4))
for k in range(5):
    plt.subplot(2, 5, k+1)
    plt.imshow(X_test[:, :, k]) # 원본 데이터

    plt.subplot(2, 5, k+6)
    plt.imshow(X_test[:, :, learning_result[k][0] - 1]) # 예측 데이터
plt.show()