K-Means++ Clustering

Introduction

K-means++ enhances the initialization phase of the K-means clustering algorithm, which partitions $n$ observations into $k$ clusters based on their proximity to the nearest cluster mean. The primary innovation of K-means++ lies in its method for selecting initial cluster centroids in a manner that improves the convergence speed and the quality of the final clustering solution.

Background and Theory

The standard K-means algorithm is sensitive to the initial choice of centroids, where poor selections can lead to suboptimal clustering results. K-means++ addresses this issue by spreading out the initial centroids, thus reducing the probability of converging to a local minimum.

Mathematical Foundations

K-means++ aims to minimize the same objective function as K-means, which is the within-cluster sum of squares (WCSS). The objective function is given by:

Here, $J$ is the objective to be minimized, $k$ represents the number of clusters, $S_i$ denotes the set of points in the $i$-th cluster, $\mathbf{x}$ is a point in $S_i$, and $\mathbf{\mu}_i$ is the centroid of $S_i$.

K-means++ Initialization

The K-means++ initialization algorithm specifically focuses on the selection of the initial centroids $\mathbf{\mu}_i$ to optimize the above objective. The steps are:

1. Select the First Centroid:
   • Randomly pick the first centroid $\mathbf{\mu}_1$ from the dataset.
2. Distance Calculation for Each Data Point:
   • For each data point $\mathbf{x}$, compute the distance squared to the nearest already chosen centroid, denoted as $D(\mathbf{x})^2$.
3. Probabilistic Centroid Selection:
   • Select each subsequent centroid $\mathbf{\mu}_i$ from the dataset with a probability proportional to $D(\mathbf{x})^2$, enhancing the chances of picking centroids that are far from existing ones.
4. Repeat Until k Centroids are Chosen:
   • Continue steps 2 and 3 until all $k$ centroids are selected.

This initialization method is formalized as:

where $P(\mathbf{x}_i)$ is the probability of selecting data point $\mathbf{x}_i$ as the next centroid, and $n$ is the total number of data points.

Procedural Steps After Initialization

With the centroids initialized via K-means++, the algorithm proceeds with the standard K-means steps:

1. Cluster Assignment: Assign each observation to the cluster with the nearest centroid.
2. Centroid Update: Recompute the centroid of each cluster to be the mean of the points assigned to the cluster.
3. Convergence Check: Repeat the assignment and update steps until the centroids stabilize (i.e., their positions do not significantly change between iterations) or a predefined number of iterations is reached.

Implementation

Parameters

• n_clusters: int
  Number of clusters
  
• max_iter: int, default = 100
  Number of iteration
  

Examples

Test on synthesized dataset with 7 Gaussian blobs:

from luma.clustering.kmeans import KMeansClusteringPlus
from luma.visual.evaluation import ClusterPlot
from luma.metric.clustering import SilhouetteCoefficient

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

X, y = make_blobs(n_samples=500, 
                  centers=7, 
                  cluster_std=1.2, 
                  random_state=10)

kmp = KMeansClusteringPlus(n_clusters=7, max_iter=300)
kmp.fit(X)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

clst = ClusterPlot(kmp, X)
clst.plot(ax=ax1)

sil = SilhouetteCoefficient(X, kmp.labels)
sil.plot(ax=ax2, show=True)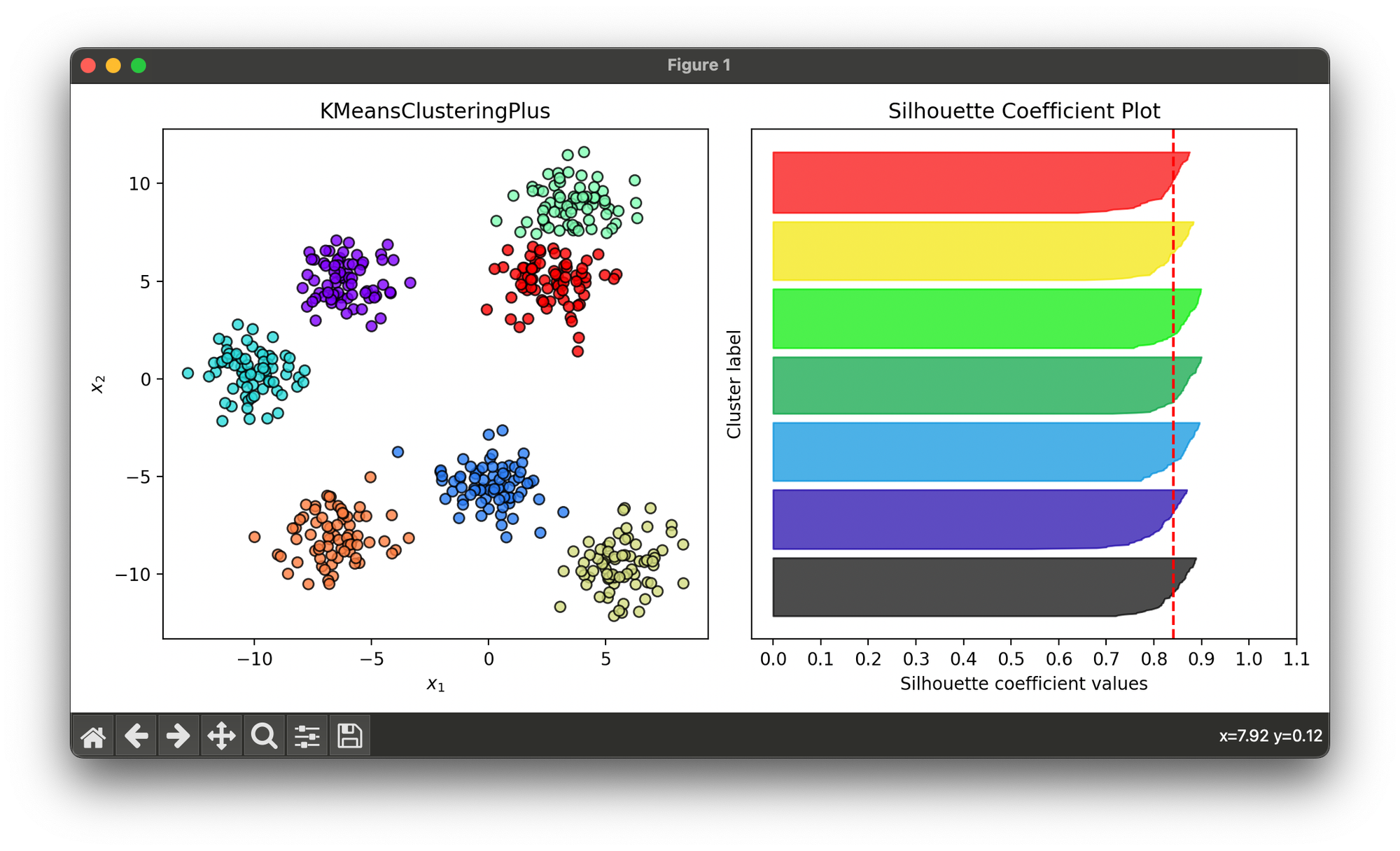

Applications and Strengths

• Improved Efficiency: By carefully selecting initial centroids, K-means++ tends to converge faster and requires fewer iterations.
• Higher Quality Clustering: Reduces the likelihood of poor clusterings due to unfortunate initial centroids.
• Widely Applicable: Useful in any domain where K-means is applicable, including document clustering, market segmentation, and image segmentation.

Limitations

• Computational Overhead: The initialization process is more computationally intensive than random initialization.
• Choice of k: The algorithm does not inherently solve the challenge of choosing the optimal number of clusters $k$.

Advanced Topics

• Hybrid and Parallel Implementations: To address the computational overhead, parallel computing techniques can be applied to the initialization process, and hybrid strategies can combine K-means++ with other optimization methods.
• Determining k: Methods like the silhouette score, the elbow method, and gap statistics can be employed in conjunction with K-means++ to help determine the most appropriate $k$.

References

1. Arthur, D., & Vassilvitskii, S. (2007). "k-means++: The Advantages of Careful Seeding". Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics.