K-Medians Clustering

Introduction

K-Medians clustering is a partitioning technique that divides a dataset into (K) groups or clusters by minimizing the median distance between points in each cluster and a designated central point. Unlike K-Means, which minimizes the mean or average distance to the cluster centroid, K-Medians focuses on the median, making it more robust to outliers and noise in the data. This algorithm is particularly useful in scenarios where the data distribution is not symmetric or when the mean is not a good representative of the central tendency due to outliers.

Background and Theory

Clustering is a method of unsupervised learning that groups similar data points together based on a defined similarity or distance metric. The K-Medians algorithm is an iterative approach that seeks to partition a dataset into $K$ non-overlapping subgroups (clusters) such that each data point belongs to the cluster with the nearest median.

Mathematical Foundations

The objective of K-Medians is to minimize the sum of distances between points and their respective cluster medians. Given a dataset $X = \{x_1, x_2, \cdots, x_n\}$ of $n$ points in a $d$-dimensional space, the goal is to find $K$ clusters $C = \{C_1, C_2, \cdots, C_K\}$ and their medians $M = \{m_1, m_2, \cdots, m_K\}$ to minimize the objective function:

where $\lVert x - m_i \rVert$ denotes the distance between point $x$ and the median $m_i$ of cluster $C_i$. The distance can be any metric, but the Manhattan distance (L1 norm) is typically used.

Procedural Steps

1. Initialization: Select $K$ initial medians either randomly or based on some heuristic.
2. Assignment: Assign each data point to the cluster whose median is closest to the point. This step is performed using the chosen distance metric.
3. Update: For each cluster, update its median by calculating the median of all points assigned to the cluster across each dimension.
4. Convergence Check: Repeat the assignment and update steps until the medians no longer change, or a maximum number of iterations is reached, indicating convergence.

Mathematical Formulations

Distance Metric

The Manhattan distance between two points $x = (x_1, x_2, \cdots, x_d)$ and $y = (y_1, y_2, \cdots, y_d)$ in a $d$-dimensional space is defined as:

Median Update

The median of a cluster $C_j$ for each dimension is updated by sorting the points in $C_j$ along that dimension and selecting the middle value if the number of points is odd, or the average of the two middle values if even.

Implementation

Parameters

• n_clusters: int
  Number of clusters
  
• max_iter: int, default = 100
  Number of iteration
  

Examples

Test on synthesized blob dataset with comparison between K-Medians and K-Means:

from luma.clustering.kmeans import KMeansClustering, KMediansClustering
from luma.visual.evaluation import DecisionRegion

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

X, y = make_blobs(n_samples=500, 
                  centers=5, 
                  cluster_std=1.0, 
                  random_state=10)

kmed = KMediansClustering(n_clusters=5, max_iter=100)
kmed.fit(X)

kmp = KMeansClustering(n_clusters=5, max_iter=100)
kmp.fit(X)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

dec_kmed = DecisionRegion(kmed, X, kmed.labels)
dec_kmed.plot(ax=ax1)

dec_kmp = DecisionRegion(kmp, X, kmp.labels)
dec_kmp.plot(ax=ax2, show=True)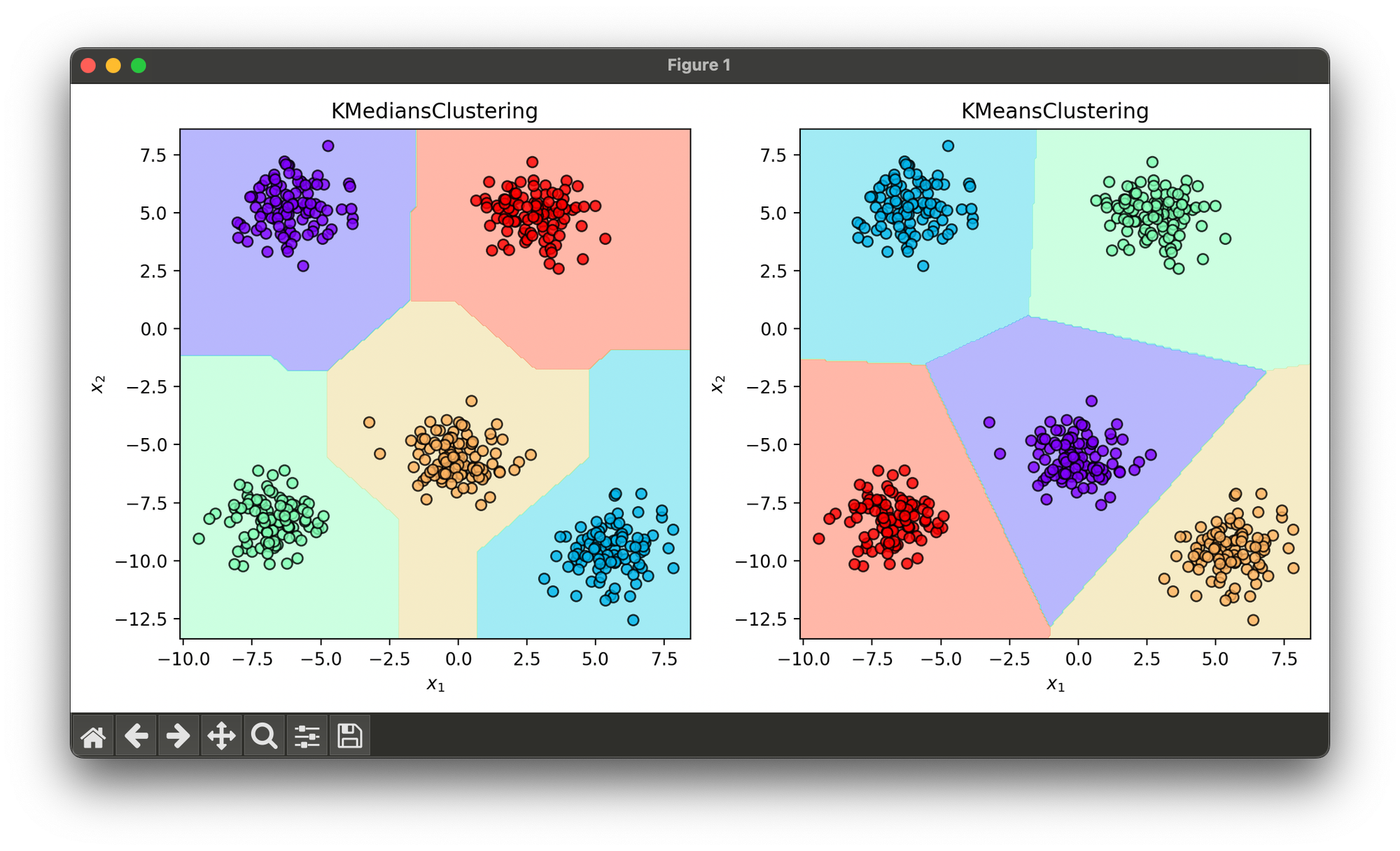

Applications

• Market Segmentation: Grouping customers based on purchase history, preferences, or demographic data.
• Document Clustering: Organizing documents into topics based on content similarity.
• Image Segmentation: Partitioning an image into segments based on pixel similarity for further analysis or processing.
• Anomaly Detection: Identifying outliers by their distance to the nearest cluster median.

Strengths and Limitations

Strengths

• Robustness: Less sensitive to outliers compared to K-Means due to the use of medians.
• Flexibility: Can be used with various distance metrics to suit different types of data.

Limitations

• Computation: Finding the exact median can be more computationally intensive than calculating the mean.
• Sensitivity to Initial Selection: The initial choice of medians can significantly affect the final clustering result.
• Difficulty in Handling High-dimensional Data: As with many clustering algorithms, performance may degrade in high-dimensional spaces due to the curse of dimensionality.

Advanced Topics

• Initialization Methods: Exploring different strategies for selecting initial medians to improve robustness and convergence speed.
• Scalability Enhancements: Techniques such as parallel processing and data sampling to handle large datasets efficiently.
• Integration with Other Clustering Methods: Combining K-Medians with hierarchical clustering for improved clustering hierarchies and insights.

References

1. Kaufman, Leonard, and Peter J. Rousseeuw. "Finding groups in data: an introduction to cluster analysis." John Wiley & Sons, 2009.
2. Bradley, Paul S., Usama M. Fayyad, and Cory A. Reina. "Scaling clustering algorithms to large databases." Proceedings of the fourth international conference on knowledge discovery and data mining, AAAI Press, 1998.