K-Medoids Clustering

Introduction

K-Medoids is a clustering algorithm similar to K-Means, with the primary difference being the choice of centroids. In K-Medoids, centroids are actual data points from the dataset, known as medoids, making it more robust to noise and outliers compared to K-Means. This algorithm is particularly useful in scenarios where an actual representative (medoid) is needed from the dataset or when the dataset contains outliers that might skew the mean.

Background and Theory

Clustering is a technique used in unsupervised learning to group similar objects into clusters. K-Medoids, also known as the Partitioning Around Medoids (PAM) algorithm, aims to minimize the sum of dissimilarities between points labeled to be in a cluster and a point designated as the center of that cluster.

Mathematical Foundations

Given a dataset $X = \{x_1, x_2, \cdots, x_n\}$ consisting of $n$ objects, K-Medoids clustering seeks to partition $X$ into $K$ clusters $C = \{C_1, C_2, \cdots, C_K\}$. The objective is to minimize the total dissimilarity between each object and the medoid of its cluster. The medoid is defined as the object in the cluster that has the smallest total dissimilarity with all other objects in the cluster.

The objective function can be formally defined as:

where $d(x, m_i)$ is the dissimilarity measure (usually Euclidean distance, but other distances can be used) between an object $x$ and the medoid $m_i$ of its cluster $C_i$.

Procedural Steps

1. Initialization: Select $K$ initial medoids from the dataset.
2. Assignment Step: Assign each object to the closest medoid, forming $K$ clusters.
3. Update Step: For each cluster, select a new medoid by minimizing the total dissimilarity between the medoid and all objects in the cluster.
4. Repeat: Repeat the assignment and update steps until the medoids no longer change or a predefined number of iterations is reached, indicating convergence.

Mathematical Formulations

Dissimilarity Measure

The choice of dissimilarity measure $d(x, y)$ is crucial. The most common choice is the Euclidean distance for numerical data, defined as:

where $x = (x_1, x_2, \cdots, x_n)$ and $y = (y_1, y_2, \cdots, y_n)$ are two points in an $n$-dimensional space.

Medoid Update

The new medoid for a cluster $C_j$ is selected by:

This ensures that the new medoid is the most centrally located object in the cluster with respect to the chosen dissimilarity measure.

Implementation

Parameters

• n_clusters: int
  Number of clusters
  
• max_iter: int, default = 300
  Number of iteration
  

Examples

Test on reduced iris dataset and searched optimal number of clusters via elbow method:

from luma.reduction.linear import PCA
from luma.clustering.kmeans import KMedoidsClustering
from luma.metric.clustering import Inertia
from luma.visual.evaluation import ClusterPlot

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import numpy as np

X, y = load_iris(return_X_y=True)

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

scores, labels, models = [], [], []
for i in range(2, 10):
    km = KMedoidsClustering(n_clusters=i,
                            max_iter=300,
                            random_state=42)
    km.fit(X_pca)    
    scores.append(Inertia.score(X_pca, km.medoids))
    labels.append(km.labels)
    models.append(km)

def derivate_inertia(scores: list) -> list:
    diff = [0.0]
    for i in range(1, len(scores) - 1):
        diff.append(scores[i - 1] - scores[i + 1])
    
    diff.append(0.0)
    return diff

d_scores = derivate_inertia(scores)
best_n = np.argmax(d_scores)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

clst = ClusterPlot(models[best_n], X_pca)
clst.plot(ax=ax1)

ax2.plot(range(2, 10), scores, marker='o', label='Inertia')
ax2.plot(range(2, 10), d_scores, marker='o', label='Absolute Derivative')

ax2.set_title('Inertia Plot')
ax2.set_xlabel('Number of Clusters')
ax2.set_ylabel('Inertia')
ax2.legend()
ax2.grid()

plt.tight_layout()
plt.show()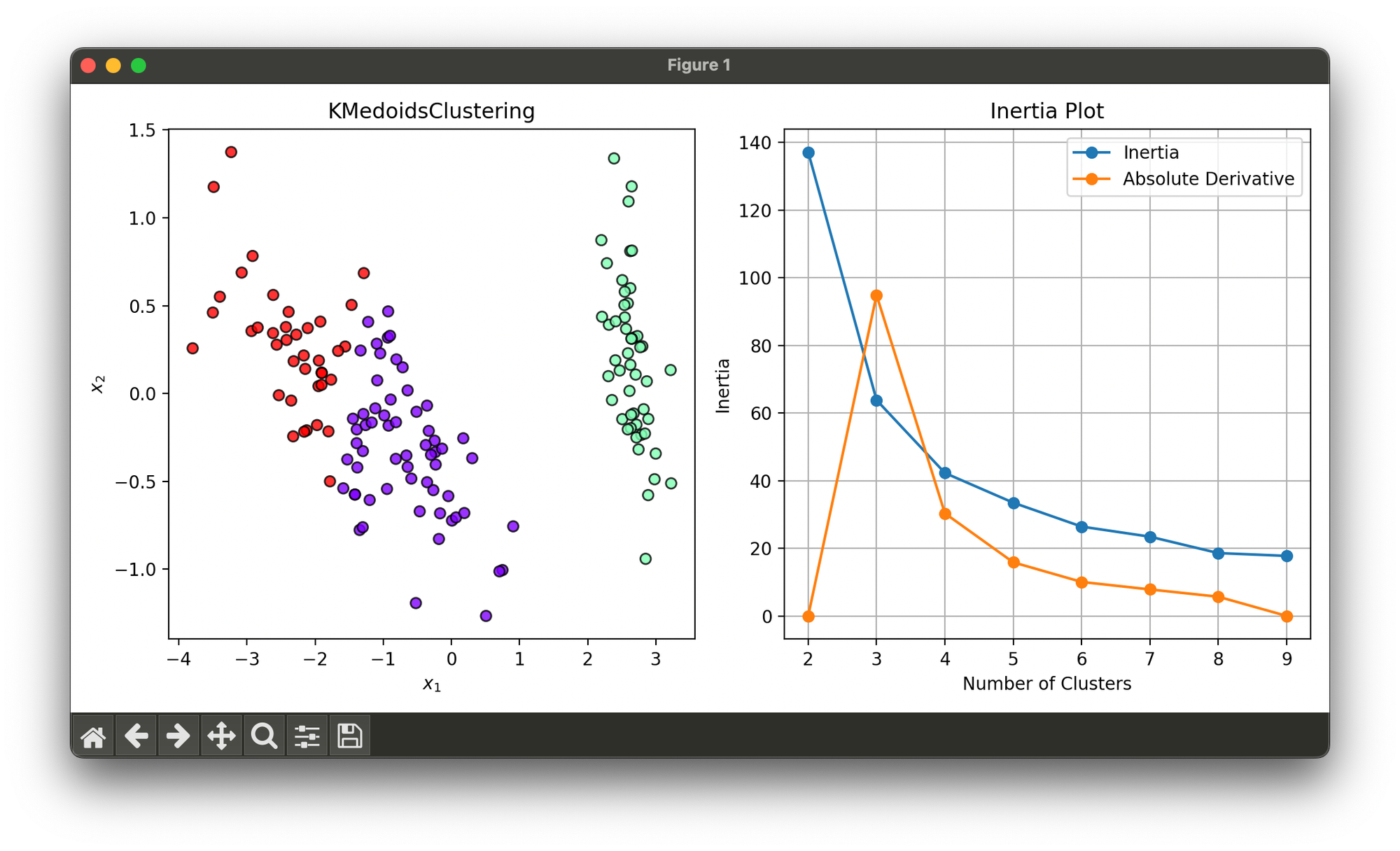

Applications

• Customer Segmentation: Grouping customers based on buying behavior or preferences for targeted marketing.
• Document Clustering: Organizing documents into groups of similar topics for information retrieval systems.
• Anomaly Detection: Identifying unusual data points by analyzing the distances to the nearest medoid.
• Image Segmentation: Grouping pixels into segments to simplify image analysis tasks.

Strengths and Limitations

Strengths

• Robustness to Outliers: By using medoids as cluster centers, K-Medoids is less sensitive to outliers compared to K-Means.
• Flexibility with Distance Measures: Can work with any distance metric, making it suitable for different types of data.

Limitations

• Computational Complexity: The algorithm can be computationally expensive, especially for large datasets, due to the cost of evaluating all potential medoids.
• Dependence on Initial Selection: The final clustering result can be sensitive to the initial selection of medoids.
• Fixed Number of Clusters: Like K-Means, K-Medoids requires specifying the number of clusters $K$ in advance, which may not be known beforehand.

Advanced Topics

• Optimization Techniques: Methods like the CLARA (Clustering Large Applications) and CLARANS (Clustering Large Applications based upon RANdomized Search) algorithms have been developed to improve the scalability and efficiency of K-Medoids.
• Dynamic Clustering: Extensions of K-Medoids that allow for dynamic adjustment of the number of clusters based on the data.
• Hybrid Approaches: Combining K-Medoids with other clustering techniques or dimensionality reduction methods to enhance performance and interpretability.

References

1. Kaufman, Leonard, and Peter J. Rousseeuw. "Clustering by means of medoids." In Statistical Data Analysis Based on the L1 Norm and Related Methods, pp. 405-416. North-Holland, 1987.
2. Park, Hae-Sang, and Chi-Hyuck Jun. "A simple and fast algorithm for K-medoids clustering." Expert Systems with Applications 36, no. 2 (2009): 3336-3341.