Mini-Batch K-Means Clustering

Introduction

Mini-Batch K-Means is a variant of the K-Means clustering algorithm that aims to reduce the computational cost by using small, random samples of the data (mini-batches) for each iteration of the algorithm, instead of the full dataset. This approach significantly speeds up the convergence time and is particularly effective for large datasets, making it a popular choice for scalable machine learning applications.

Background and Theory

K-Means is a widely used clustering algorithm that partitions a dataset into (K) clusters by minimizing the variance within each cluster. The Mini-Batch K-Means algorithm introduces an optimization by processing small subsets of the dataset in each iteration, which drastically reduces the amount of computation needed to converge to a solution.

Mathematical Foundations

The objective function of the K-Means algorithm is to minimize the sum of squared distances between each data point and the centroid of its assigned cluster. For a dataset $X = \{x_1, x_2, \cdots, x_n\}$ with $n$ data points, the objective function is defined as:

where $C_i$ represents the set of points in cluster $i$, $\mu_i$ is the centroid of cluster $i$, and $\lVert x - \mu_i \rVert^2$ is the squared Euclidean distance between point $x$ and centroid $\mu_i$.

Procedural Steps

1. Initialization: Randomly select $K$ centroids from the dataset as the initial cluster centers.
2. Mini-Batch Processing: At each iteration, randomly sample a mini-batch of $b$ data points from the dataset.
3. Cluster Assignment: Assign each data point in the mini-batch to the nearest centroid.
4. Centroid Update: Update the centroids of the clusters based on the newly assigned points from the mini-batch.
5. Iteration: Repeat steps 2-4 until the centroids stabilize or a predefined number of iterations is reached.

Mathematical Formulations

Centroid Update

The centroid update in Mini-Batch K-Means is performed using an incremental update formula to account for the mini-batch processing. The new centroid $\mu_i'$ after processing a mini-batch is calculated as:

where $\bar{x}_i$ is the mean of the points in the mini-batch assigned to cluster $i$, and $\eta$ is the learning rate, which controls the extent to which the centroids are updated. The learning rate may decrease over time to ensure convergence.

Implementation

Parameters

• n_clusters: int
  Number of clusters
  
• batch_size: int, default = 100
  Size of a single batch
  
• max_iter: int, default = 100
  Number of iteration
  

Examples

Test on reduced wine dataset and find optimal number of clusters via inertia elbow plot:

from luma.preprocessing.scaler import StandardScaler
from luma.reduction.linear import PCA
from luma.clustering.kmeans import MiniBatchKMeansClustering
from luma.metric.clustering import Inertia
from luma.visual.evaluation import ClusterPlot

from sklearn.datasets import load_wine
import matplotlib.pyplot as plt
import numpy as np

X, y = load_wine(return_X_y=True)

sc = StandardScaler()
X_std = sc.fit_transform(X)

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_std)

scores, labels, models = [], [], []
for i in range(2, 10):
    km = MiniBatchKMeansClustering(n_clusters=i,
                                   batch_size=100,
                                   max_iter=100)
    km.fit(X_pca)    
    scores.append(Inertia.score(X_pca, km.centroids))
    labels.append(km.labels)
    models.append(km)

def derivate_inertia(scores: list) -> list:
    diff = [0.0]
    for i in range(1, len(scores) - 1):
        diff.append(scores[i - 1] - scores[i + 1] / 2)
    
    diff.append(0.0)
    return diff

d_scores = derivate_inertia(scores)
best_n = np.argmax(d_scores)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

clst = ClusterPlot(models[best_n], X_pca, cmap='viridis')
clst.plot(ax=ax1)

ax2.plot(range(2, 10), scores, marker='o', label='Inertia')
ax2.plot(range(2, 10), d_scores, marker='o', label='Absolute Derivative')

ax2.set_title('Inertia Plot')
ax2.set_xlabel('Number of Clusters')
ax2.set_ylabel('Inertia')
ax2.legend()
ax2.grid()

plt.tight_layout()
plt.show()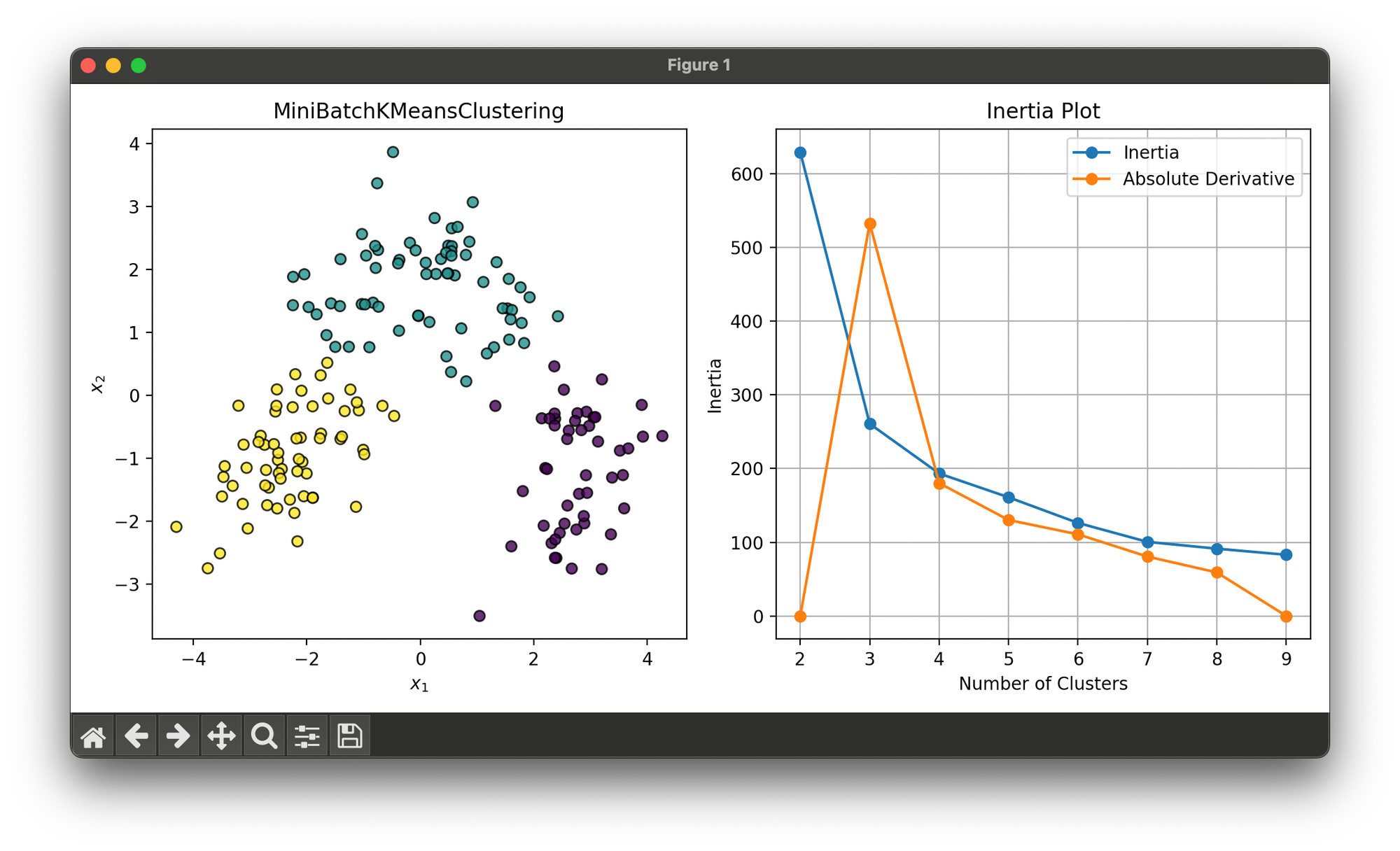

Applications

• Large-scale Data Clustering: Efficiently clustering large datasets that are infeasible to process with standard K-Means due to computational or memory constraints.
• Real-time Data Streaming: Clustering streaming data where the entire dataset is not available upfront and data arrives in increments.
• Image Quantization: Reducing the number of colors in an image for compression purposes without significantly affecting visual quality.

Strengths and Limitations

Strengths

• Scalability: Highly efficient for large datasets, reducing computational time and memory usage.
• Flexibility: Suitable for online clustering tasks where data arrives in a stream.

Limitations

• Approximation Quality: The centroids found by Mini-Batch K-Means may not be as accurate as those found by the standard K-Means due to the stochastic nature of the algorithm.
• Parameter Sensitivity: The choice of mini-batch size and learning rate can significantly affect the algorithm's performance and convergence.

Advanced Topics

• Optimal Mini-Batch Size: Investigating the impact of mini-batch size on the convergence rate and clustering quality.
• Learning Rate Strategies: Adaptive learning rate adjustments over iterations to improve convergence stability.
• Hybrid Approaches: Combining Mini-Batch K-Means with other clustering or dimensionality reduction techniques for enhanced performance in complex datasets.

References

1. Sculley, David. "Web-scale k-means clustering." Proceedings of the 19th international conference on World wide web. 2010.
2. Bradley, Paul S., Usama M. Fayyad, and Cory A. Reina. "Scaling clustering algorithms to large databases." Proceedings of the fourth international conference on knowledge discovery and data mining, AAAI Press, 1998.