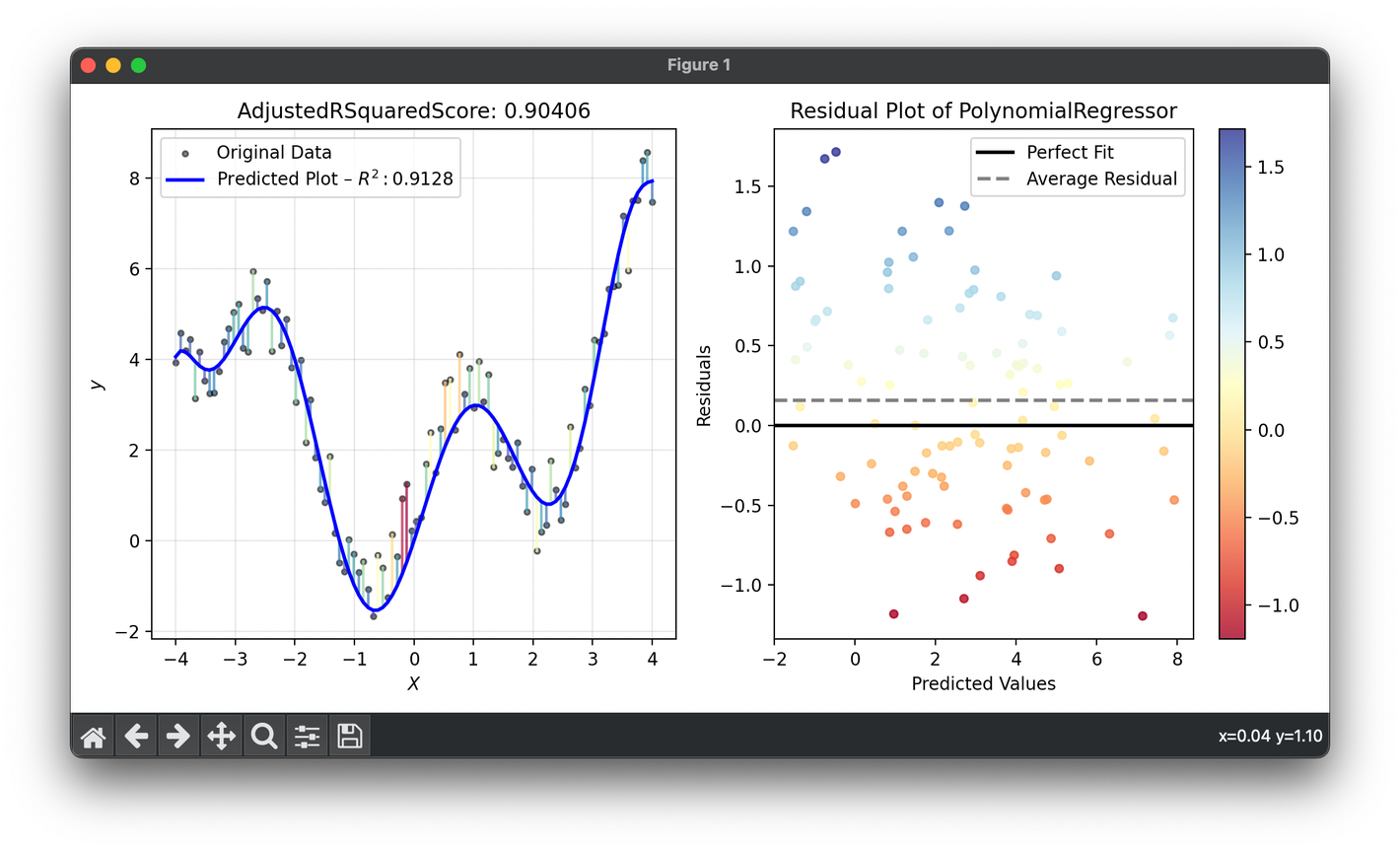
Adjusted R-Sqaured($R^2_\text{adj}$) Score

Introduction

Adjusted $R^2$ (Adjusted Coefficient of Determination) enhances the traditional $R^2$ metric by adjusting for the number of predictors in a regression model. This adjustment provides a more accurate reflection of the model's explanatory power, particularly when comparing models with different numbers of independent variables. It's a critical measure in statistical analysis for ensuring that the addition of variables to a model is truly improving its predictive capability, rather than just capitalizing on chance.

Background and Theory

While $R^2$ quantifies how well a model explains the variability of the dependent variable, it has a tendency to increase as more predictors are added, regardless of their actual relevance to the model. This can lead to overfitting, where a model appears to perform better on the training data but does not generalize well to unseen data. The adjusted $R^2$ compensates for this by penalizing the addition of irrelevant predictors, thus offering a more balanced measure of model performance.

The formula for adjusted $R^2$ is:

where:

• $R^2$ is the coefficient of determination,
• $n$ is the sample size,
• $p$ is the number of independent variables in the model.

The adjusted $R^2$ can decrease if the addition of a variable does not improve the model's explanatory power sufficiently, making it a valuable tool for model selection and validation.

Applications

• Model Selection: Identifying the most appropriate model by comparing the adjusted $R^2$ values across different models with varying numbers of predictors.
• Validation: Assessing the true explanatory power of a model, ensuring it is not inflated by the mere addition of more variables.
• Research and Development: In fields such as economics, psychology, and environmental science, where understanding the influence of multiple factors on a dependent variable is crucial.

Strengths and Limitations

Strengths

• Penalizes Model Complexity: Adjusted $R^2$ discourages the unnecessary addition of predictors that do not contribute significantly to the model's explanatory power.
• Improves Comparability: Makes it more feasible to compare models with different numbers of predictors on an equal footing.

Limitations

• Not a Definitive Measure of Goodness: A higher adjusted $R^2$ does not guarantee that a model is the best choice for prediction or inference.
• Relative, Not Absolute: Adjusted $R^2$ is still a relative measure of fit and must be considered alongside other model evaluation metrics and domain knowledge.

Advanced Topics

• Thresholds for Model Selection: While adjusted $R^2$ is useful for model comparison, setting specific thresholds for its value as a criterion for model selection can be arbitrary and should be informed by the specific context and objectives of the analysis.
• Interaction with Other Metrics: Adjusted $R^2$ is often used alongside other metrics such as AIC (Akaike Information Criterion) and BIC (Bayesian Information Criterion) for a comprehensive evaluation of model performance.

References

1. Draper, N. R., & Smith, H. (1998). Applied Regression Analysis. Wiley.
2. James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning. Springer.