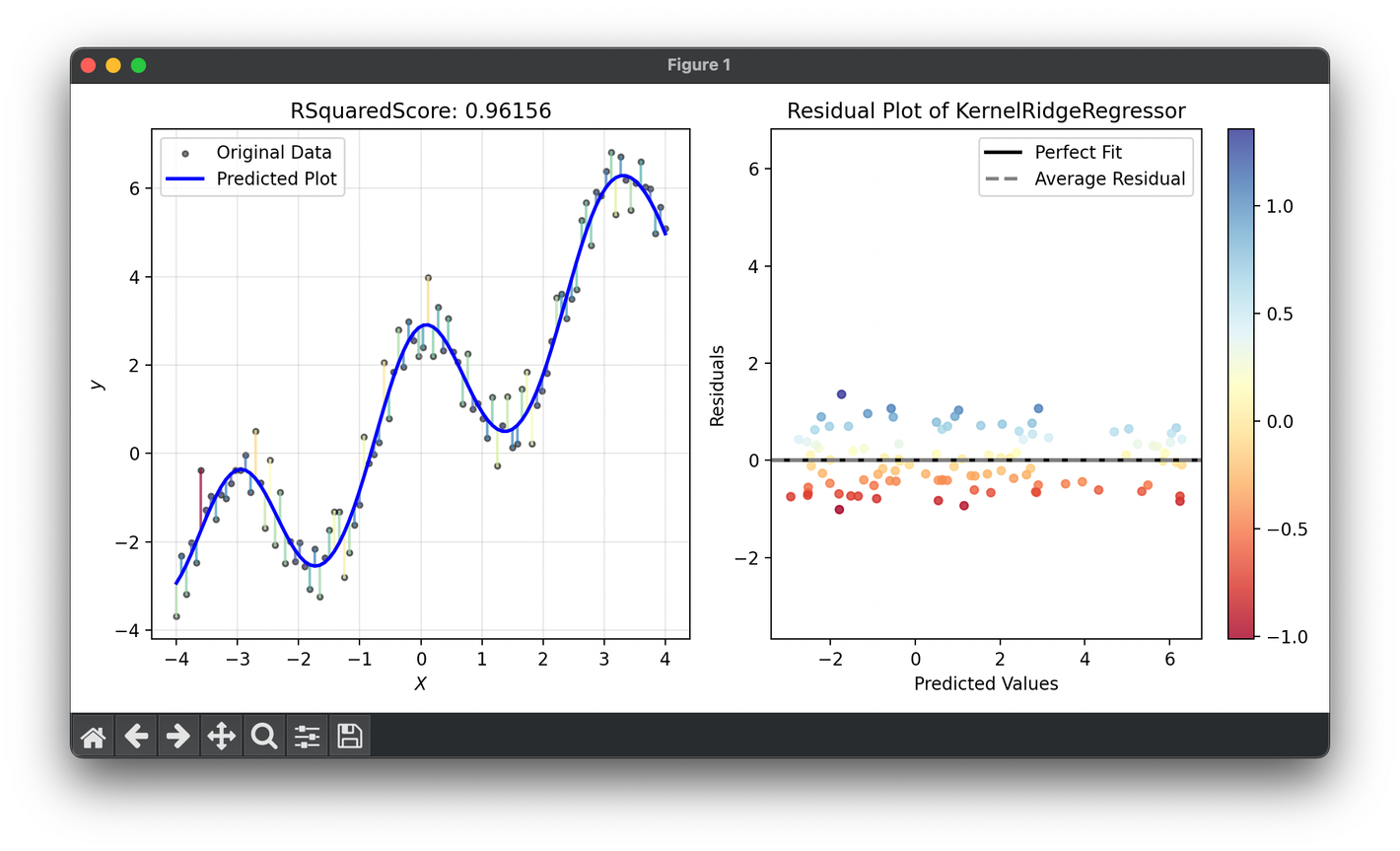
R-Squared($R^2$) Score

Introduction

$R^2$, also known as the coefficient of determination, is a statistical measure used to assess the goodness of fit of a regression model. It quantifies how well the independent variables explain the variability of the dependent variable, offering insights into the percentage of the data's variance accounted for by the model. $R^2$ is widely utilized in predictive analytics and modeling to evaluate the predictive power and accuracy of regression models.

Background and Theory

The $R^2$ value ranges from 0 to 1, where 0 indicates that the model explains none of the variability of the response data around its mean, and 1 indicates that the model explains all the variability. It is calculated based on the proportion of the total variation of outcomes explained by the model. The formula for $R^2$ is given by:

where:

• $SSR$ (sum of squares of residuals): $\sum_{i=1}^{n} (y_i - \hat{y}_i)^2$,
• $SST$ (total sum of squares): $\sum_{i=1}^{n} (y_i - \bar{y})^2$,
• $y_i$ is the actual value,
• $\hat{y}_i$ is the predicted value,
• $\bar{y}$ is the mean of actual values, and
• $n$ is the number of observations.

Applications

• Predictive Modeling: Assessing the performance of regression models in various fields, such as economics, finance, environmental science, and social sciences.
• Model Comparison: Comparing the explanatory power of different models on the same dataset.
• Feature Selection: Identifying the most relevant predictors by examining the change in $R^2$ when variables are added or removed from the model.

Strengths and Limitations

Strengths

• Interpretability: $R^2$ is a straightforward measure that provides insight into the proportion of the variance explained by the model.
• Comparability: It allows for the comparison of the explanatory power of models on the same dataset.

Limitations

• Non-indicative of Predictive Accuracy: A high $R^2$ does not necessarily mean the model has high predictive accuracy. It only indicates the proportion of variance explained.
• Sensitive to Overfitting: Adding more predictors to a model can artificially inflate $R^2$, even if those variables do not improve the model’s predictive capability.
• Not Suitable for All Models: $R^2$ is not appropriate for evaluating models where the assumptions of linear regression are violated or for models not based on linear assumptions.

Advanced Topics

• Adjusted $R^2$: To account for the potential overfitting with the inclusion of multiple predictors, the adjusted $R^2$ modifies the calculation to reflect the number of predictors in the model. It provides a more accurate measure for comparing models with a different number of variables.
  $R^2_{\text{adj}} = 1 - \frac{(1-R^2)(n-1)}{n-p-1}$
  where $p$ is the number of predictors and $n$ is the sample size.
  
• Partial $R^2$: Evaluates the contribution of one or more predictors to the model while controlling for the presence of other variables.

References

1. James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning. Springer.
2. Draper, N. R., & Smith, H. (1998). Applied Regression Analysis. Wiley.