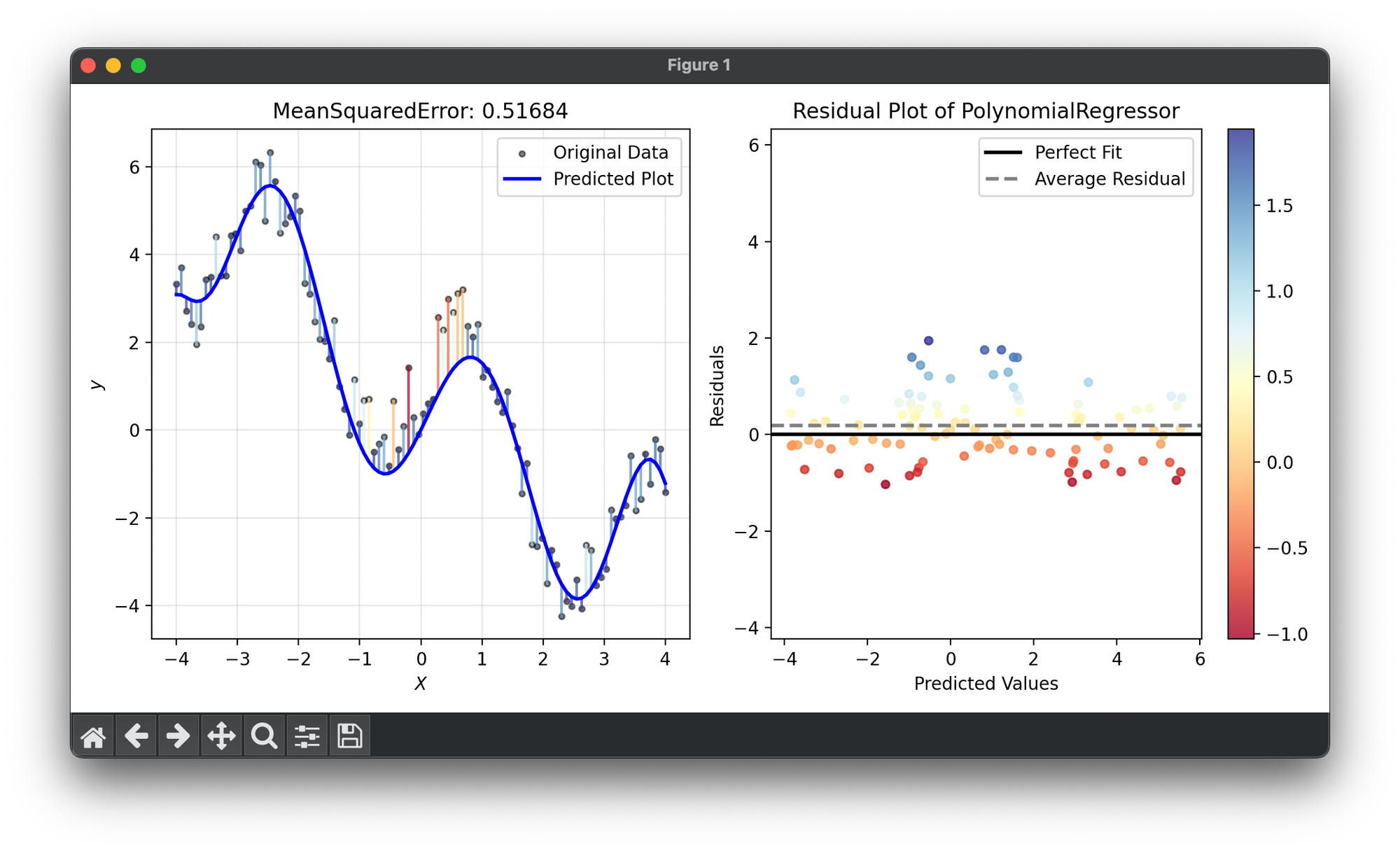
Mean Squared Error (MSE)

Introduction

Mean Squared Error (MSE) is a statistical measure used to evaluate the performance of regression models. It calculates the average of the squares of the errors, which are the differences between the predicted and actual values. MSE is a crucial metric because it highlights not just the magnitude of the errors but also amplifies the impact of larger errors due to the squaring process. This characteristic makes MSE sensitive to outliers and can be particularly useful in applications where large errors are undesirable.

Background and Theory

The MSE is derived from the theory of least squares, a standard approach in regression analysis that minimizes the sum of the squared differences between the observed and predicted values. The squaring of the errors ensures that all errors are positive and that larger errors are penalized more heavily than smaller ones. The mathematical expression for MSE is:

where:

• $n$ is the total number of observations,
• $y_i$ represents the actual values, and
• $\hat{y}_i$ represents the predicted values.

Procedural Steps

1. Prediction: Generate predictions for the dataset using the regression model.
2. Calculate Squared Errors: Compute the square of the difference between each predicted value and the actual value.
3. Average the Squared Errors: Calculate the mean of these squared errors. This mean is the MSE.

Applications

MSE is widely applied in various fields, including but not limited to:

• Machine Learning: For evaluating and tuning regression models.
• Finance: In the assessment of risk and return models.
• Engineering: For control system optimization and signal processing.
• Meteorology: In weather prediction models to improve forecast accuracy.

Strengths and Limitations

Strengths

• Sensitivity to Large Errors: By squaring the errors, MSE is particularly useful in highlighting and penalizing large discrepancies between predicted and actual values.
• Differentiability: The square function is continuously differentiable, making MSE advantageous in optimization problems, especially in gradient descent algorithms.

Limitations

• Impact of Outliers: The squaring term can make MSE very sensitive to outliers, potentially skewing the evaluation of a model's performance.
• Scale Dependence: MSE values are not directly interpretable in the same units as the target variable, especially when compared to metrics like MAE.

Advanced Topics

• Root Mean Squared Error (RMSE): A derivative metric of MSE, RMSE takes the square root of MSE, offering a more interpretable scale (the same units as the target variable) and maintaining sensitivity to large errors.
• Normalized MSE (NMSE): Adjusting MSE relative to a baseline or the variance of the dataset, providing a standardized measure of error.

References

1. Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning. Springer.
2. Montgomery, D.C., Jennings, C.L., & Kulahci, M. (2015). Introduction to Time Series Analysis and Forecasting. Wiley.