Mean Absolute Percentage Error (MAPE)

Introduction

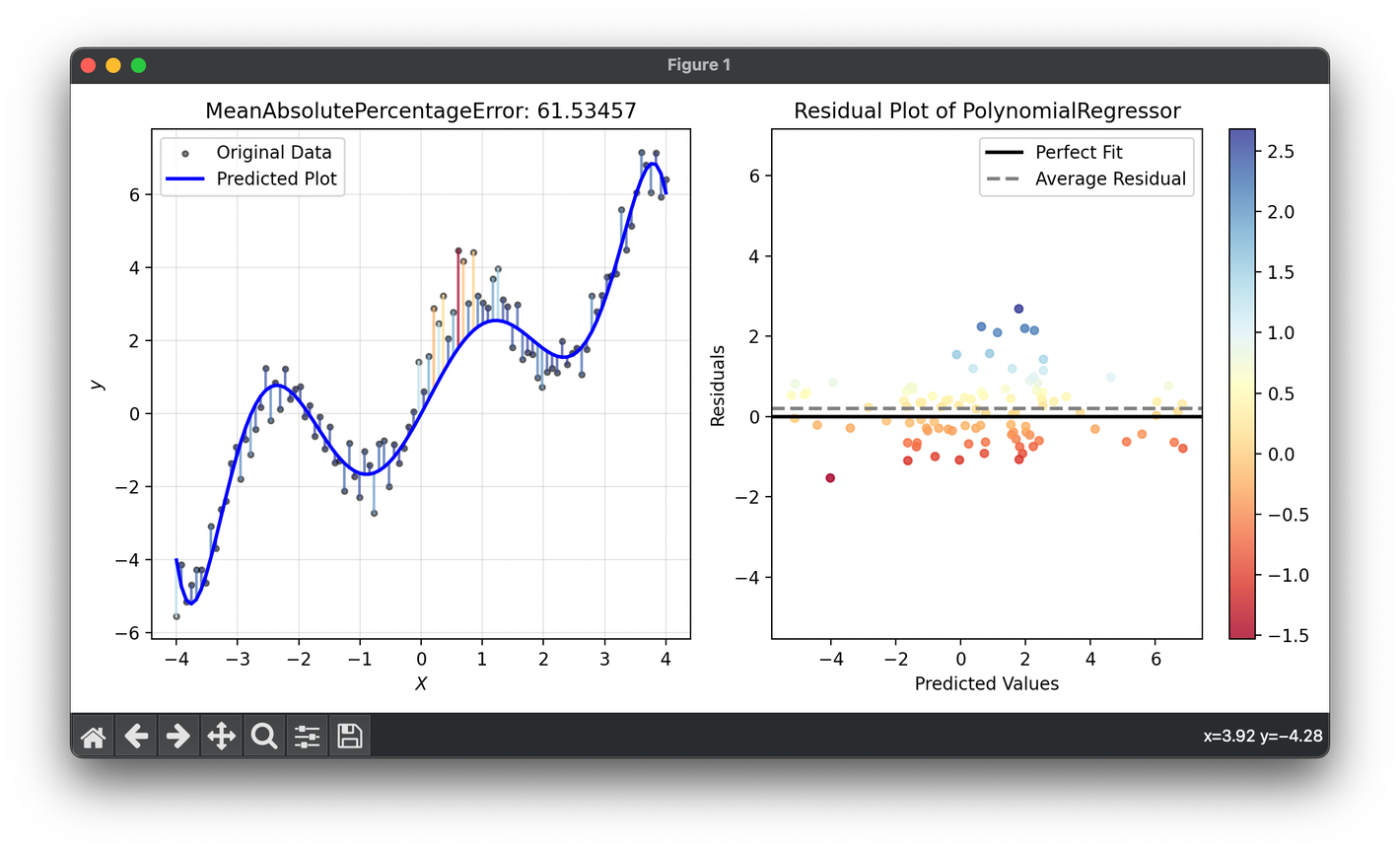
Mean Absolute Percentage Error (MAPE) is a statistical measure often used to assess the accuracy of forecast models. By expressing prediction errors as a percentage, MAPE provides a clear and intuitive understanding of the error magnitude relative to the actual values. This metric is particularly useful in fields where comparisons of error across datasets of varying scales and units are necessary.

Background and Theory

MAPE quantifies the average absolute percent error between predicted and actual values, offering a scale-independent measure of accuracy. This characteristic makes it especially valuable for comparing the performance of forecasting models across different data sets or scales. It is calculated as follows:

where:

• $n$ is the number of observations,
• $y_i$ is the actual value for the $i^\text{th}$ observation, and
• $\hat{y}_i$ is the predicted value for the $i^\text{th}$ observation.

Procedural Steps

1. Compute Predictions: Generate predictions for the dataset using the model.
2. Calculate Absolute Percentage Errors: For each pair of predicted and actual values, calculate the absolute value of the difference divided by the actual value, then multiply by 100 to get a percentage.
3. Average the Errors: Calculate the mean of these percentage errors to obtain the MAPE.

Applications

MAPE is widely applicable across various industries and fields for performance evaluation of forecasting models, including:

• Finance and Economics: For predicting stock prices, economic indicators, and financial metrics.
• Supply Chain and Logistics: In forecasting demand, inventory levels, and supply chain disruptions.
• Energy Sector: For predicting energy production and consumption.
• Public Health: In forecasting disease spread and patient admissions.

Strengths and Limitations

Strengths

• Interpretability: The percentage-based error makes MAPE highly interpretable, as it is easy to understand how large the prediction errors are relative to the actual values.
• Scale Independence: Being a relative error measure, MAPE allows for comparisons across datasets with different scales or magnitudes.

Limitations

• Undefined for Zero Actuals: MAPE becomes undefined or infinitely large when any actual value is zero, which can be a limitation in datasets with zero values.
• Asymmetry: MAPE can be more sensitive to underpredictions than overpredictions, as the denominator (actual values) does not change symmetrically with over- and underpredictions.
• High Variability for Small Actual Values: Small actual values can lead to very high errors, disproportionately affecting the MAPE.

Advanced Topics

• Modified MAPE: To address the issue with zero actual values, variations of MAPE, such as the symmetric MAPE (sMAPE), have been developed.
• Weighted MAPE: For datasets where certain observations are more important, a weighted MAPE can provide a more nuanced error metric.

References

1. Makridakis, Spyros. "Accuracy measures: theoretical and practical concerns." International Journal of Forecasting 9.4 (1993): 527-529.
2. Hyndman, Rob J., and Koehler, Anne B. "Another look at measures of forecast accuracy." International journal of forecasting 22.4 (2006): 679-688.