Root Mean Squared Error (RMSE)

Introduction

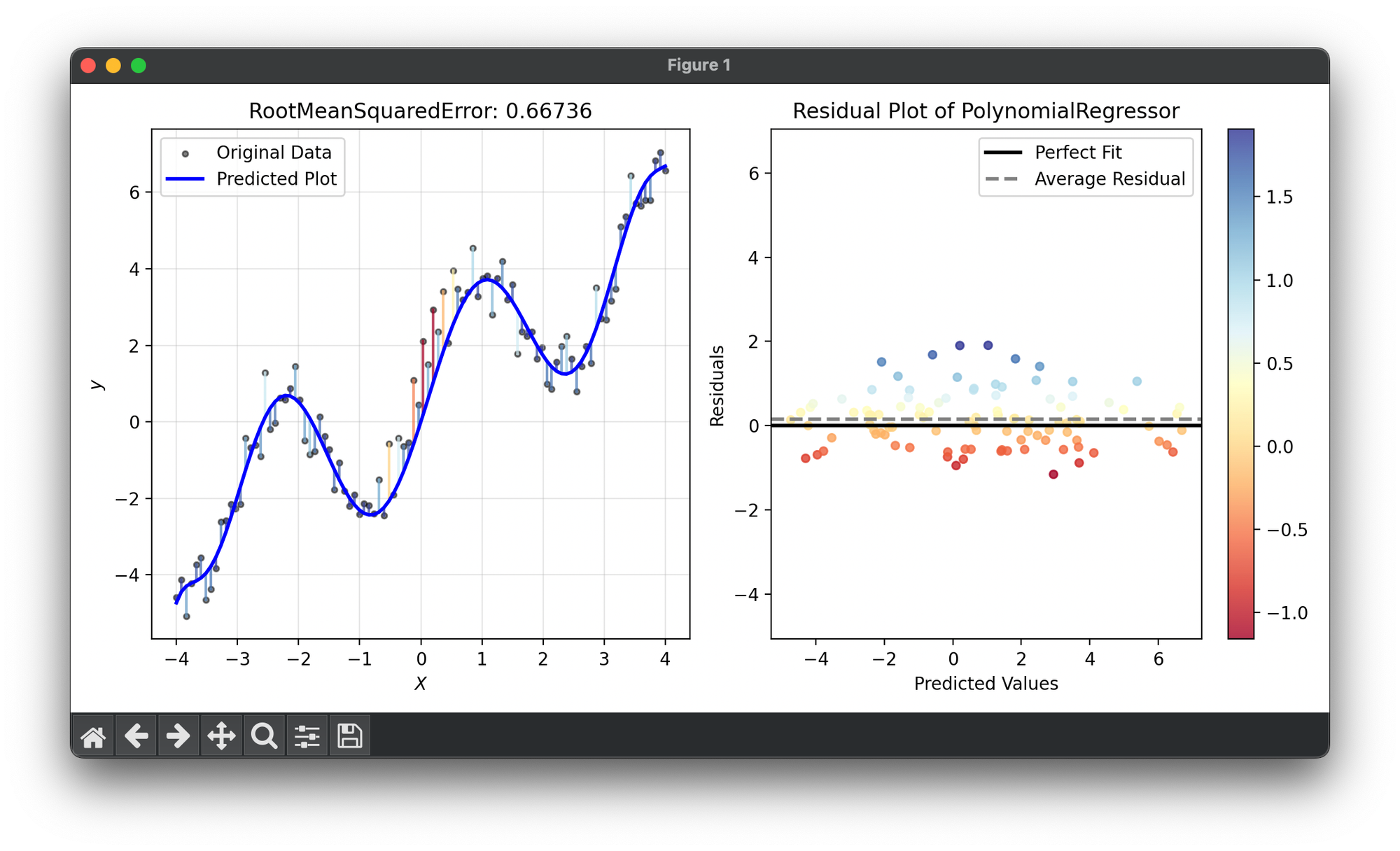
Root Mean Squared Error (RMSE) is a standard way to measure the error of a model in predicting quantitative data. Fundamentally, it represents the square root of the second sample moment of the differences between predicted values and observed values or the quadratic mean of these differences. RMSE is widely used in statistics, forecasting, and regression analysis to quantify the prediction error of a model.

Background and Theory

RMSE is derived from the Mean Squared Error (MSE), which calculates the average of the squares of the errors between the predicted and actual values. By taking the square root of MSE, RMSE converts the error metric back to the same units as the original data, making it more interpretable. This process retains the sensitivity of MSE to larger errors due to the squaring of the error terms, making RMSE particularly useful in contexts where it is important to penalize larger errors more severely.

Mathematical Formulation

The RMSE is calculated using the formula:

Where:

• $n$ is the number of observations,
• $y_i$ is the actual value of the $i^\text{th}$ observation, and
• $\hat{y}_i$ is the predicted value for the $i^\text{th}$ observation.

Procedural Steps

1. Compute Predictions: Use the model to generate predictions for the dataset.
2. Determine Squared Errors: For each prediction, calculate the squared difference between the predicted and the actual value.
3. Calculate MSE: Find the mean of these squared differences to obtain the MSE.
4. Compute RMSE: Take the square root of the MSE to determine the RMSE.

Applications

RMSE finds application in a variety of fields where the accuracy of predictions and forecasts is critical, such as:

• Machine Learning: For evaluating the performance of regression models.
• Remote Sensing: In assessing the accuracy of spatial data predictions.
• Energy Forecasting: For predicting demand and supply in energy markets.
• Climate Science: In evaluating the accuracy of temperature and precipitation models.

Strengths and Limitations

Strengths

• Interpretability: RMSE is in the same units as the target variable, making it easier to understand and interpret compared to MSE.
• Sensitivity to Large Errors: Like MSE, RMSE is particularly sensitive to large errors, helping to identify models that might be performing poorly on outlier or extreme values.

Limitations

• Influenced by Outliers: The sensitivity to large errors means that RMSE can be heavily influenced by outliers, which can sometimes provide a misleading representation of model performance.
• Not Normalized: RMSE does not provide a normalized metric, making it challenging to compare across datasets with different scales or units.

Advanced Topics

• Normalized RMSE (NRMSE): To facilitate comparison across models or datasets, RMSE can be normalized, typically by dividing by the range or standard deviation of the observed values.
• RMSE in Cross-validation: Utilizing RMSE as a metric in cross-validation procedures to assess model stability and generalizability.

References

1. Hyndman, Rob J., and Koehler, Anne B. "Another look at measures of forecast accuracy." International journal of forecasting 22.4 (2006): 679-688.
2. Chai, Tianfeng, and Draxler, Roland R. "Root mean square error (RMSE) or mean absolute error (MAE)? – Arguments against avoiding RMSE in the literature." Geoscientific Model Development 7.3 (2014): 1247-1250.