[딥러닝] Bootstrap Your Own Latent : A New Approach to Self-Supervised Learning (BYOL)

Ethan·2023년 10월 22일
BYOLContrastive LearningDL
0

Papers Review

목록 보기
15/18
post-thumbnail

Published in NIPS 2020

요약

  • Positive dataset만을 사용하여 important features를 잡아낼 수 있음
    - image augmentation strategy에 덜 의존적
    - real representation을 바로 생성할 수 있음

  • Momentum Encoder와 Batch Normalization을 사용하여 mode collapse가 발생하지 않음

Background

Contrastive Learning이란 representation 공간에서 positive pair간의 거리는 줄이고 negative pair간의 거리는 멀어지게 유도하여 모델이 positive sample들의 특징을 학습하도록 하는 방법론입니다. Dimensionality Reduction by Learning an Invariant Mapping (IEEE, 2006)에서 처음 제시된 Contrastive loss에 그 바탕을 두고 있습니다.

Contrastive learning에서 negative sample을 사용하는 이유는 Mode collapse를 막기 위해서입니다. Negative sample에서 추출되는 정보들을 일종의 regularization처럼 취급하여 올바른 학습 방향으로 learning curve를 보정하기 때문에 L2 distance, consine similarity처럼 주어진 sample 간의 거리나 유사도를 측정하는 metric이 loss function에 포함되는 경우가 많습니다.

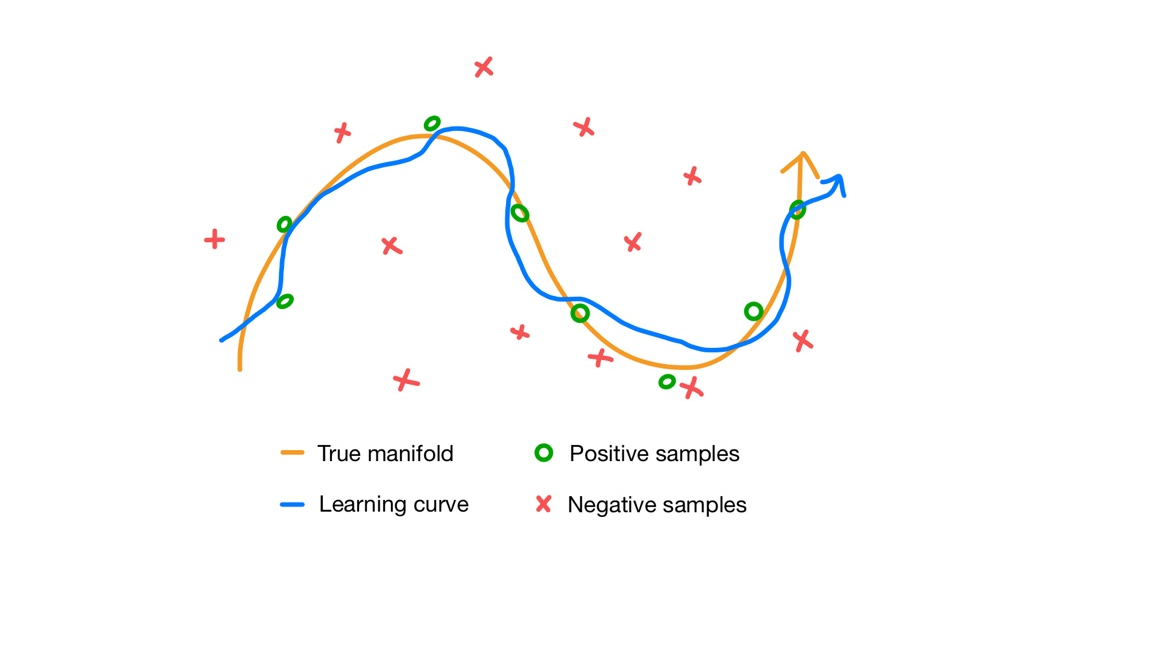
위 그림처럼 positive sample에 가까워지고 negative sample에서 멀어지도록 학습을 진행하면 결과적으로 학습한 representation이 true manifold로 수렴하도록 유도할 수 있습니다.

일반적으로 negative sample을 만들기 위해 data augmentation에 의존하기 때문에 상당한 메모리를 요구하며, 충분한 정보를 얻기 위해 large batch size를 사용해야 합니다. 어떤 augmentation strategy를 사용하느냐가 성능에 크게 관여하며, 양질의 negative sample을 정의하기 어렵다는 문제도 존재합니다.

Motivation

그렇다면 negative samples를 학습에 사용하지 않으면 어떻게 될까요? 대부분의 경우 negative sample에 대한 항을 제외하면 별도의 regularization term이 없기 때문에 positive sample에 overfitting되면서 mode collapse가 발생하게 됩니다.

Mode collapse는 기본적으로 local optimum problem입니다. 흔히 'constant vector를 출력한다'고 표현하는데 모델의 출력이 바뀌지 않는다는 뜻입니다. 데이터가 불균형하거나, constraint가 불완전하거나, 학습 데이터가 부족하거나, 초기화가 잘못되었거나 등 다양한 원인이 있을 수 있지만 어쨌든 결과적으로 local point boundary에서 벗어나지 못하고 있는 것이죠.

이를 해결하는 가장 간단한 방법 중 하나는 generator network의 가중치를 랜덤하게 초기화시킨 후 고정하는 것입니다. 생성 목표에 대해 아는 게 거의 없는 상태를 유지하는 셈인데, loss function의 관점에서 보면 오차가 크기 때문에(=기울기가 커지므로) 학습량이 증가하게 되어 local region에 매몰되지 않습니다. 당연하지만 오차가 크다면 성능이 좋지 않다는 뜻이므로 일반적으로는 이러한 네트워크를 사용할 이유가 없습니다.

그런데 여기서 갑자기 이상한 현상이 나타납니다. 바로 동일한 랜덤 초기화 네트워크 A와 B가 있을 때 A가 출력한 representation을 예측하도록 B를 학습시킨 후, B가 출력한 representation을 downstream task을 위한 representation으로 사용하면 정확도가 급격하게 상승한 것입니다.

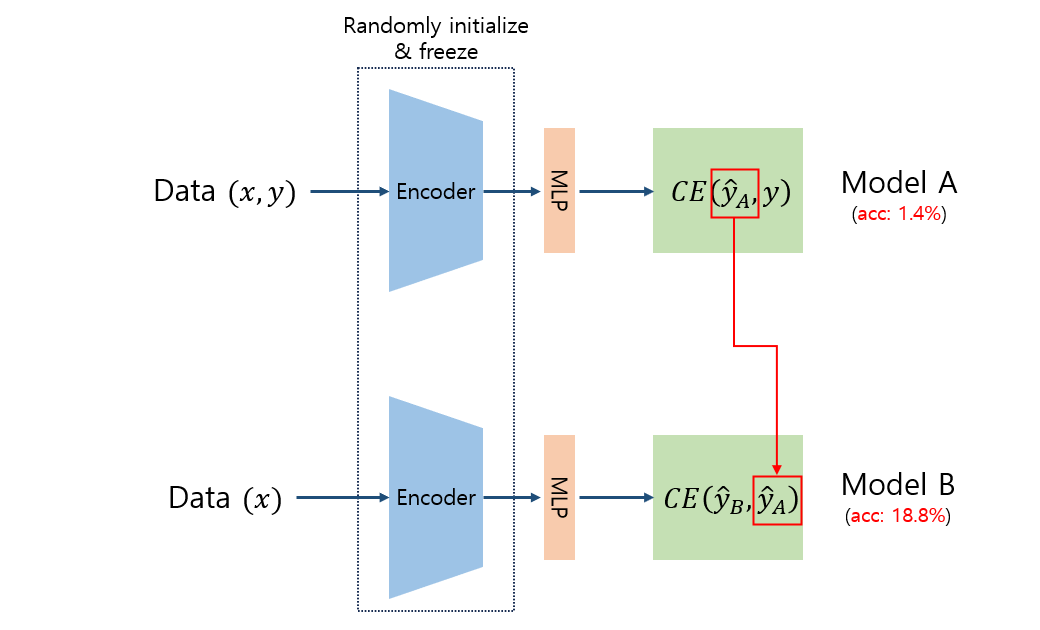
실험 결과에 따르면 randomly initialized network A의 초기 정확도는 고작 1.4%밖에 되지 않지만, 해당 representation을 학습한 network B가 생성한 representation의 정확도는 18.8%로 무려 17.4%가 상승하였습니다. 저자들은 이러한 실험 결과에 착안하여 BYOL을 제안했습니다. (여기서 bootstrap은 통계적인 기법을 말하는 게 아니라, 매번 새로운 y^\hat{y}을 생성하기 때문에 붙은 이름입니다.)

사실 위 실험 결과는 매우 이상합니다. A는 분명 매우 낮은 품질의 representation을 생성했는데, 이를 따라하도록 학습한 B의 representation의 품질이 좋아졌다는 말이니까요. 이는 BYOL의 한계점 중 하나로, 본문에서는 이러한 현상이 왜 발생하는지에 대해 구체적인 분석은 제시하지 않고 있습니다.

다만, 뇌과학 분야에서는 인간이 실제로 혼자서 잘못된 방향으로 학습을 시작하더라도 시간이 지나면 올바른 방향으로 학습이 진행된다고 알려져 있습니다. 이와 비슷한 맥락으로 이해해볼 수도 있겠습니다.

Model Architecture

Objectives

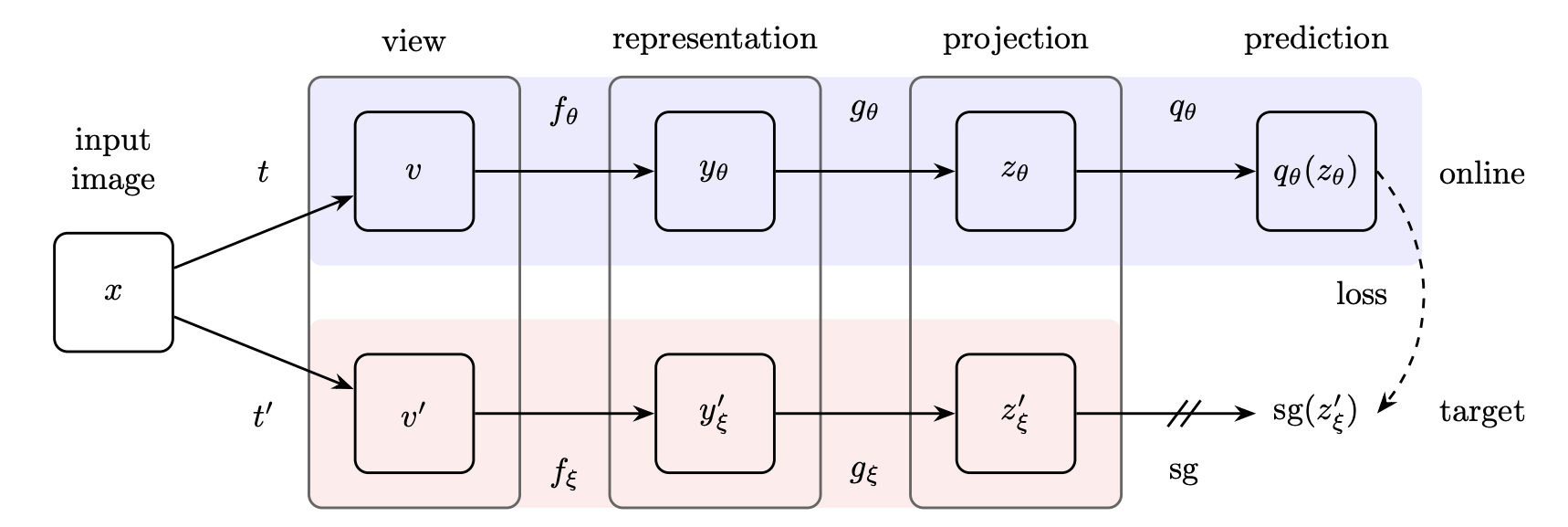
앞선 실험 결과를 바탕으로 저자들은 위와 같이 target / online 2개의 asymmetric network로 이루어진 구조를 설계했습니다.

BYOL의 목적은 downstream task에 사용할 수 있는 yθy_\theta를 얻는 것입니다. 주어진 image set x∼Dx \sim D에 대해 임의의 augmentation distribution t∼T,t′∼T′t\sim T, t'\sim T'가 적용된다고 하면 v≜t(x),v′≜t′(x)v\triangleq t(x), v'\triangleq t'(x)가 됩니다.

이렇게 얻은 augmented vectors v,v′v, v'를 encoder function ff에 입력해주면 representation vector yθy_\theta를 얻을 수 있고, 이를 다시 projector function gg에 입력하면 projection vector zθ≜gθ(y)z_\theta\triangleq g_\theta(y)를 얻게 됩니다. 같은 방법으로 target network를 거쳐 yξ′,zξ′y'_\xi, z'_\xi도 만들 수 있습니다.

이후 online network는 target network에서 생성한 projection vector zξ′z'_\xi에 대해 prediction module qθq_\theta를 통해 예측을 수행합니다. 이 때 각 벡터 zξ′z'_\xi와 qθ(zθ)q_\theta(z_\theta)를 모두 normalize해 줍니다.

qθ(zθ)‾=qθ(zθ)∥qθ(zθ)∥2,zξ‾′=zξ′∥zξ′∥2\overline{q_\theta(z_\theta)}=\frac{q_\theta(z_\theta)}{\lVert q_\theta(z_\theta)\rVert_2},\quad \overline{z_\xi}'=\frac{z'_\xi}{\lVert z'_\xi\rVert_2}

결과적으로 predictor qθq_\theta의 loss function은 다음과 같이 normalized target projection zξ‾′\overline{z_\xi}'과 normalized online prediction qθ(zθ)‾\overline{q_\theta(z_\theta)} 두 벡터의 MSE 형태가 됩니다. (Scaled cosine distance로도 해석할 수 있습니다.)

Lθ,ξ≜∥qθ(zθ)‾−zξ‾′∥22=(qθ(zθ)‾−zξ‾′)T(qθ(zθ)‾−zξ‾′)=(qθ(zθ)‾)2+(zξ‾′)2−2⋅qθ(zθ)‾T zξ‾′=2−2⋅⟨qθ(zθ),zξ′⟩∥qθ(zθ)∥2⋅∥zξ′∥2(1)\begin{aligned} L_{\theta,\xi}&\triangleq \lVert\overline{q_\theta(z_\theta)}-\overline{z_\xi}'\rVert_2^2\\ \\ &= (\overline{q_\theta(z_\theta)}-\overline{z_\xi}')^T(\overline{q_\theta(z_\theta)}-\overline{z_\xi}') \\ \\ &= (\overline{q_\theta(z_\theta)})^2+(\overline{z_\xi}')^2-2\cdot\overline{q_\theta(z_\theta)}^T\ \overline{z_\xi}' \\ \\ &= 2-2\cdot{\langle q_\theta(z_\theta),z_\xi'\rangle \over \lVert q_\theta(z_\theta)\rVert_2\cdot\lVert z_\xi'\rVert_2}\qquad(1) \end{aligned}

이후 식 (1)을 symmetric하게 바꾸기 위해 vv를 target network에, v′v'를 online network에 투입하여 계산한 L~θ,ξ\tilde{L}_{\theta,\xi}를 더해주면 다음과 같이 최종 loss function을 얻게 됩니다.

Lθ,ξBYOL=Lθ,ξ+L~θ,ξ(2)L^{BYOL}_{\theta,\xi}=L_{\theta,\xi}+\tilde{L}_{\theta,\xi}\qquad(2)

이 때 주의할 점이 있는데 식 (2)는 θ\theta에 대해서만 최적화되어야 합니다. ξ\xi를 업데이트하면 미래의 정보를 미리 아는 셈이 되기 때문에 data leak에 해당합니다. 대신 ξ\xi는 θ\theta의 EMA로 계산하여 업데이트해줍니다. 즉, θ\theta의 모멘텀을 이용하여 ξ\xi의 학습 방향을 올바르게 교정합니다.

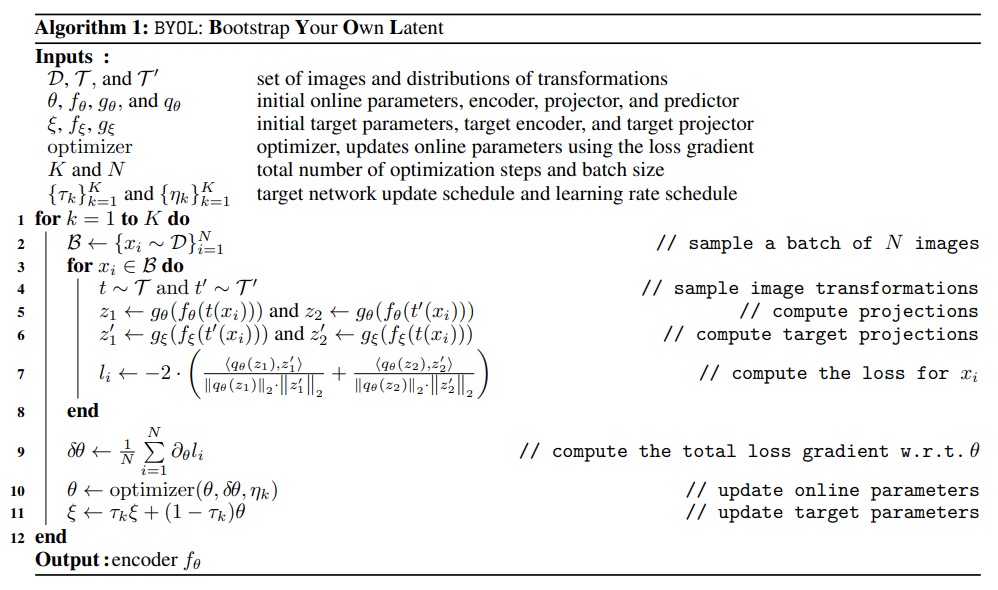
θ←optimizer(θ,∇θLθ,ξBYOL,η)andξ←τξ+(1−τ)θ η=learning rate\theta\leftarrow\text{optimizer}(\theta,\nabla_\theta L^{BYOL}_{\theta,\xi}, \eta)\quad\text{and}\quad\xi\leftarrow\tau\xi+(1-\tau)\theta\\ \ \\ \eta= \text{learning rate}

위 알고리즘을 보면 학습이 끝난 후에는 encoder function fθf_\theta만 남기고 나머지는 사용하지 않습니다. 따라서 training할 때보다 더 적은 자원으로도 inference가 가능합니다.

Mode collapse?

그런데 식 (1), (2)에는 mode collapse를 방지하기 위한 부분이 명시되어 있지 않습니다. 그렇다면 BYOL은 과연 mode collapse에서 자유로울까요?

Mode collapse이 발생하는 원인 중 하나는 모델이 positive class의 데이터를 생성하도록 학습하는 것이 아니라, loss를 최소화하도록 학습하기 때문입니다. arg min⁡θ,ξ∇θ,ξLθ,ξ\argmin_{\theta,\xi}\nabla_{\theta,\xi}L_{\theta,\xi}인 (θ∗,ξ∗)(\theta^*,\xi^*)에 도달하여 L=0L=0이 되면 더 이상 다른 정보를 고려하지 않게 되는 것이죠.

그런데 BYOL은 arg min⁡ξ∇ξLθ,ξ\argmin_\xi\nabla_{\xi}L_{\theta,\xi} 방향으로 ξ\xi를 업데이트하지 않습니다. 물론 이것만으로는 반드시 model collapse가 일어나지 않는다는 것이 보장되지 않으므로, 저자들은 (θ∗,ξ∗)(\theta^*,\xi^*)이 θ,ξ\theta,\xi 모두에 대해 동시에 optimal point가 되는 Lθ,ξL_{\theta,\xi}는 존재하지 않는다는 가설을 제시합니다.

예를 들어 GAN에서 Discriminator DD와 generator GG에 대해 D,GD, G가 '평형'을 이루는 지점에서의 파라미터 (d∗,g∗)(d^*, g^*)는 DD와 GG의 입장에서 optimal point가 아닙니다. 만약 DD의 분류 정확도가 100%라면 GG가 생성한 데이터는 실제와 동떨어진 데이터일 것이고, GG가 생성한 데이터가 완벽하게 실제 데이터와 같다면 DD의 분류 정확도는 50%로 수렴할 수밖에 없죠. 즉, DD와 GG를 동시에 최적화하는 loss function은 존재하지 않습니다. 물론 수식 상으로 BYOL에 이와 동일한 논리를 적용할 순 없지만 적어도 실험 중에는 이러한 mode collapse가 나타나지 않았다고 합니다.

Such equilibria is unstable

만약 위와 같은 equilibria가 존재한다고 해도 이는 unstable, 즉 실제로 나타나기 어렵다고 합니다. 예를 들어 online network의 predictor가 optimal할 때의 파라미터를 p∗p^*라고 하면 다음과 같이 나타낼 수 있습니다.

qθ=q∗withq∗≜arg min⁡qE[∥q(zθ)−zξ′∥22],(3) whereq∗(zθ)=E[zξ∣zθ]q_\theta=q^*\quad \text{with}\quad q^*\triangleq\argmin_q \mathbb{E}[\lVert q(z_\theta)-z'_\xi\rVert_2^2],\qquad(3)\\ \ \\ \text{where}\quad q^*(z_\theta)=\mathbb{E}[z_\xi|z_\theta]

식 (3)을 최적화하면 다음과 같습니다.

∇θE[∥q(zθ)−zξ′∥22]=∇θarg min⁡E[∥E[zξ∣zθ]−zξ′∥22] =∇θE[∑iVar(zξ,i′∣zθ)](4)\begin{aligned} \nabla_\theta\mathbb{E}[\lVert q(z_\theta)-z'_\xi\rVert_2^2] &= \nabla_\theta\argmin\mathbb{E}[\lVert \mathbb{E}[z_\xi|z_\theta]-z'_\xi\rVert_2^2]\\ \ \\ &=\nabla_\theta\mathbb{E}\left[\sum_i\text{Var}(z'_{\xi,i}|z_\theta)\right]\qquad(4) \end{aligned}

만약 online projection vector zθz_\theta가 constant vector cc를 출력한다고 가정해보겠습니다. 그러면 임의의 random variable X,Y,ZX, Y, Z에 대해 Var(X∣Y,Z)≤Var(X∣Y)\text{Var}(X|Y, Z)\leq\text{Var}(X|Y)이고 분산은 음수가 될 수 없으므로 다음이 성립합니다.

0≤Var(zξ′∣zθ)≤Var(zξ′∣c)(5)0\leq\text{Var}(z'_\xi|z_\theta)\leq\text{Var}(z'_\xi|c)\qquad(5)

즉, 데이터만 충분하다면 online projection vector zθz_\theta에서 얻는 새로운 정보를 통해 target projection vector zξ′z'_\xi를 (거의 항상) 업데이트할 수 있습니다.

0≤Var(c∣zθ)≤Var(zξ,i′∣zθ)0\leq\text{Var}(c|z_\theta)\leq\text{Var}(z'_{\xi,i}|z_\theta)

흥미로운 점은 만약 EMA를 사용하지 않고 ξ\xi에 대해 gradient descent를 적용하면(∇ξ)(\nabla_\xi) 위와 같이 target projection vector zξ′z'_\xi가 constant vector cc로 수렴하게 된다는 것입니다. 즉, 더 이상 파라미터 업데이트가 일어나지 않는 mode collapse가 발생합니다.

EMA를 활용한 파라미터 업데이트 외에도 predictor qθ(zθ)q_\theta(z_\theta) 또한 mode collapse를 방지하는 데 기여합니다. 실제로 predictor를 제거하면 바로 collapsed representation이 출력된다고 합니다.

Experiments

Implement details

  • ImageNet ILSVRC-2012 데이터셋 사용

  • SimCLR과 동일한 image augmentation 수행
    - random patch, horizontal flip, color distortion, gaussian blur 등

  • Encoder baseline으로 ResNet-50 사용
    - dim of yθy_\theta : 2048

  • Projection, Predictor는 MLP를 사용
    - dim of zθz_\theta : 4096, dim of qθ(zθ)q_\theta(z_\theta) : 256
    - linear-batchnorm-relu-linear 순으로 구성

  • Optimizer는 LARS 사용

Linear evaluation on ImageNet

Linear evaluation : 인코더를 freeze하고 linear classfier를 추가하여 성능을 평가하는 방법

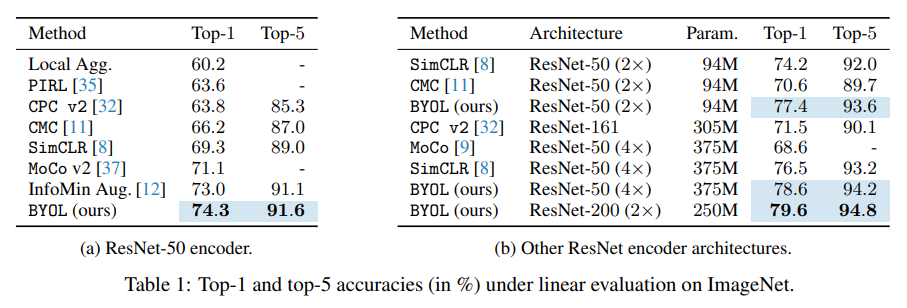
실험 결과 BYOL이 가장 높은 점수를 기록했습니다. 인코더의 레이어 수를 늘렸을 때도 BYOL이 가장 좋은 성능을 보여줍니다.

Semi-supervised training on ImageNet

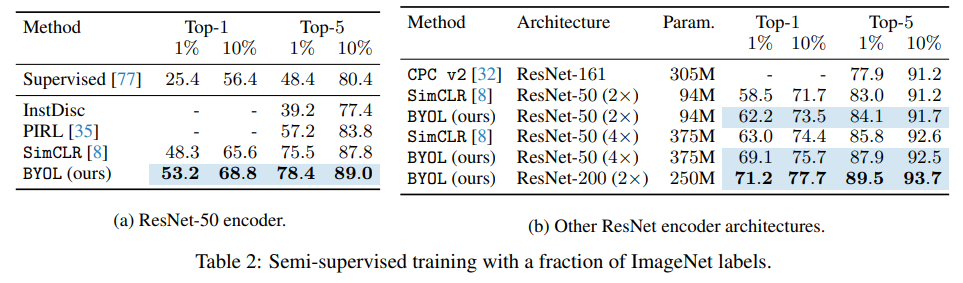
여기서 말하는 semi-supervised는 훈련 데이터 일부를 사용하여 인코더를 파인튜닝하는 것을 말합니다. 위 표는 각각 1%와 10%의 데이터의 라벨 정보를 활용하여 파인튜닝했을 때의 성능입니다.

Transfer to other classification tasks

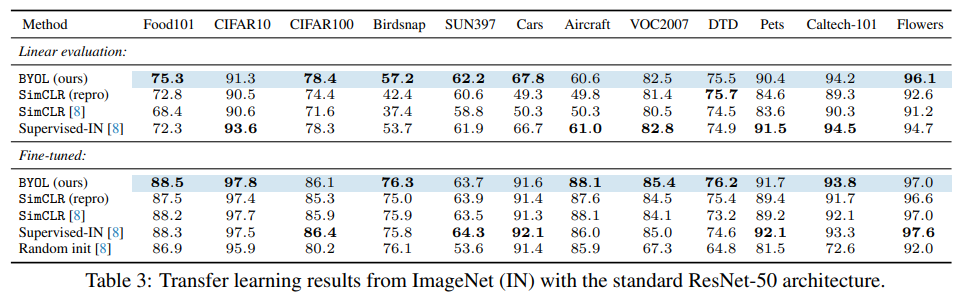
일부 데이터셋을 제외하면 대부분 BYOL이 가장 좋은 성능을 보였고, 그마저도 최고 점수를 받은 모델과 거의 차이가 나지 않는 것을 알 수 있습니다.

BYOL은 unsupervised, (implicit) self-supervised 모델이기 때문에 label 정보를 사용하지 않았는데도 label 정보를 사용한 supervised model보다 더 좋거나 비슷한 성능을 보여주고 있습니다.

Limitations

Batch normalization and BYOL

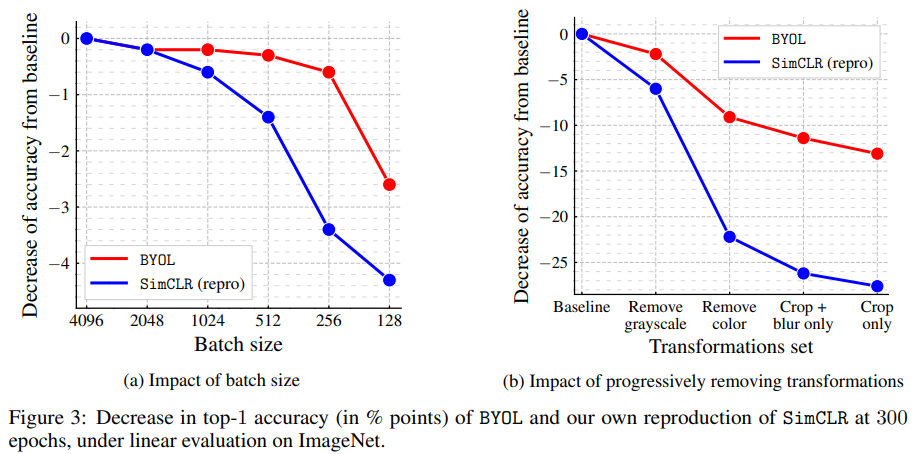
위 표를 보면 SimCLR은 augmentation strategy에 따라 성능이 크게 변화합니다. 하지만 BYOL은 성능이 SimCLR만큼 크게 움직이지는 않습니다. 물론 BYOL도 5~10% 가까이 성능이 저하되긴 하지만 개별 augmentation strategy의 난이도에 따른 변화로 납득할만한 수치입니다.

또, SimCLR은 배치 사이즈가 줄어들면 급격하게 성능이 저하되지만 BYOL은 256이상의 배치 사이즈에서는 성능이 거의 줄어들지 않습니다. 대신 256보다 작은 배치 사이즈에서는 확연하게 감소하기 시작하는데, 논문에서는 이를 batch normalization이 배치 사이즈에 영향을 받기 때문이라고 언급합니다. 즉, batchnorm이 배치 사이즈에 민감하기 때문에 성능에 악영향을 끼친다는 것이죠.

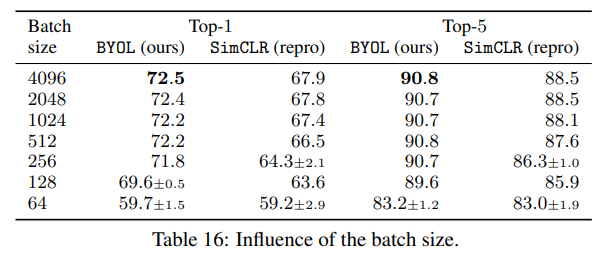
위 표에서도 배치 사이즈 256까지는 거의 성능의 변화가 없지만, 배치사이즈가 64까지 감소하면 성능이 빠르게 저하됩니다. SimCLR도 마찬가지인데, 이는 배치사이즈에 따른 성능 저하가 batchnorm layer 자체의 문제일 가능성을 암시합니다.

만약 그렇다면, batch normalization을 제거하면 성능이 향상될까요?

BatchNorm prevent mode collapse?

결론부터 말하자면, 그럴 수도 있고 아닐 수도 있습니다.

BYOL learns by asking, “how is this image different from the average image?“

Understanding self-supervised and contrastive learning with BYOL이라는 블로그 포스팅에서는 batchnorm(BN)이 mode collapse를 실질적으로 방지하는 역할이라고 주장합니다.

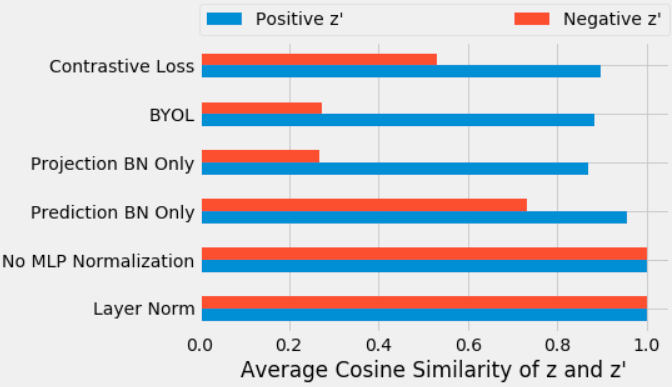
해당 블로그에서 제시한 그래프를 보면 MLP 내부에서 BN을 제거할 경우 mode collapse가 발생합니다. 반대로 projection에 BN을 달기만 해도 mode collapse가 사라지죠.

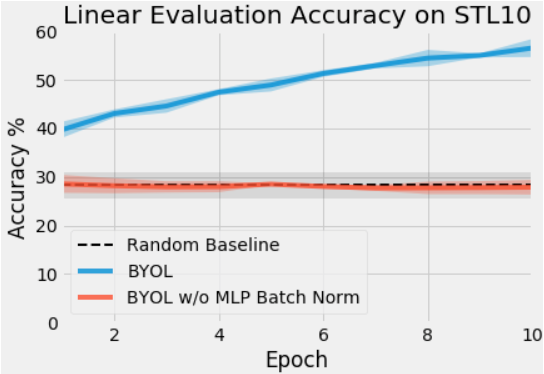
심지어 BN을 없앤 BYOL은 random initialized network와 별다른 차이가 없다(!)는 충격적인 결과도 보여줍니다.

Batch Normalization 논문을 보면 내부에서 정규화 과정을 거치면서 각 배치의 mean, var를 기준으로 representation vector에 nonlinearity를 부여하는 프로세스가 있는데, 이처럼 배치 내 데이터를 각각 해당 배치의 mode와 비교하는 과정을 거치는 것이 implicit contrastive learning의 역할을 한다는 것이 해당 블로거의 주장입니다.

BYOL works even without Batch statistics?

굉장히 흥미롭게도, 이에 대해 딥마인드 팀에서 BYOL works even without batch statistics 라는 논문을 통해서 반박을 내놓았습니다(!).

해당 논문에서는 BN이 implicit contrastive learning의 역할을 할 수 있다는 점은 부정하지 않습니다. 다만 BYOL에 들어 있는 BN은 단지 weight initialization을 위한 것이며, 위 표에서 볼 수 있듯이 초깃값을 잘 설정하면 성능에 지장이 없다고 강조합니다. 또한 BN이 아니더라도 group normalization과 weight standardization을 조합하면 좋은 성능을 얻을 수 있다고 하는데... 사실 GN+WS →\rightarrow BN과 비슷하다는 것이 흥미로운 포인트네요.

Also...

그 외에도 BYOL처럼 positive pair만으로 학습하여 좋은 성과를 거둔 Exploring Simple Siamese Representation Learning 이라던가 mode collapse의 원인을 다각도로 분석한 Understanding Self-Supervised Learning Dynamics without Contrastive Pairs 와 같은 후속 논문들이 있습니다. Self-supervised Learning 자체가 워낙 핫한 연구 분야라서, 만약 흥미가 있다면 해당 연구들을 더 살펴봐도 좋겠습니다.

참고문헌

  1. Bootstrap Your Own Latent： A New Approach to Self-Supervised Learning 리뷰
  2. [NIPS 2020] Bootstrap Your Own Latent A New Approach to Self-Supervised Learning (BYOL) 핵심 리뷰
  3. DMQA - Dive into BYOL
  4. Bootstrap your own latent
  5. Image Feature Learning - Self-Supervised Learning (2) _ Contrastive Learning
  6. Understanding self-supervised and contrastive learning with BYOL
profile
Ethan
재미있게 살고 싶은 대학원생
이전 포스트

[딥러닝] Layer Collaboration in the Forward-Forward Algorithm

다음 포스트

[신경과학] Serotonin neurons modulate learning rate through uncertainty

0개의 댓글