Intro.

다항회귀 모델로 예측해봐도 여전히 남아있는 과소적합이 찜찜한데... 도와주세요ㅠ
김 팀장🗣️ "뭐야, 높이랑 두께 데이터도 있으면서 왜 안 썼어? 선형회귀는 특성이 많을수록 효과가 뛰어나니까, 여러 개의 특성을 함께 적용해 봐!"

1. 다중 회귀

데이터 준비

• 이번엔 길이 말고 높이랑 두께까지, 특성(독립변수)이 3개로 늘어남.
• 인터넷에서 데이터를 편하게 내려받아 쓸 수 있는 pandas 라이브러리 활용!

  입력 데이터

  • pd.read_csv() : 외부의 csv 파일을 데이터프레임으로 받아오는 함수
    .to_numpy() : 넘파이 배열로 바꿔주는 메소드
    

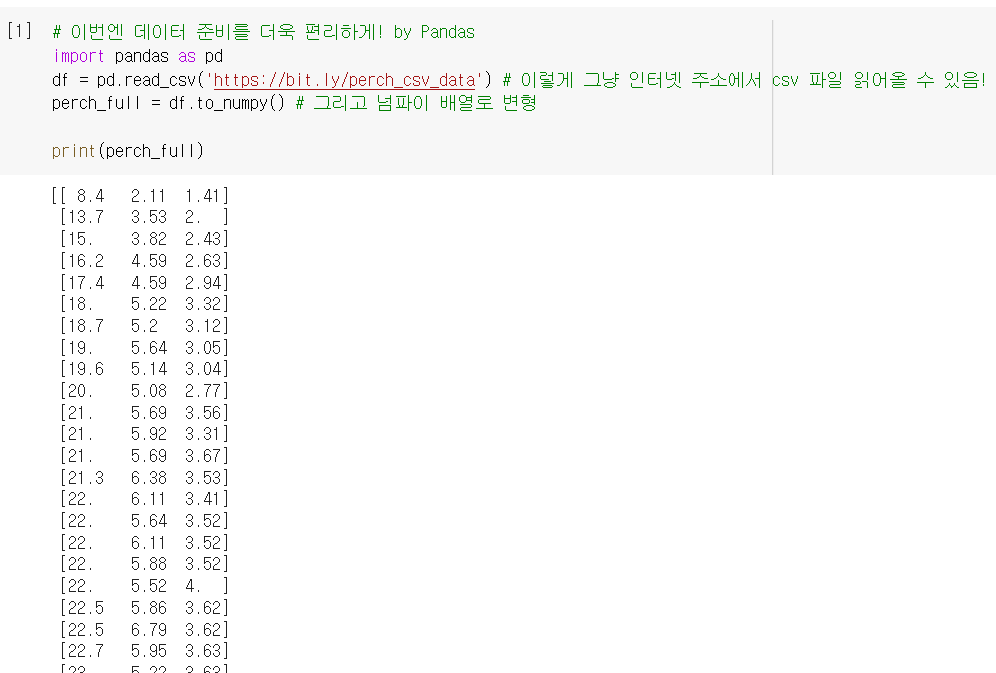
    타깃 데이터

    

    훈련/테스트 세트 분할

    

특성 공학(feature engineering)

• PolynomialFeatures() : 다항 특성을 만들어주는 변환기 클래스
• .transform() : 변환기로 데이터를 변환해주는 메소드 (❗.fit() 쓰고 써야 함)
• include_bias=False : 절편 항을 무시해주는 옵션
• .get_feature_names_out() : 변환된 특성 종류를 확인할 수 있는 메소드
  (x0, x1, x2는 각각 1, 2, 3번째 특성을 가리키는 문자임. = 길이, 높이, 두께)

다중회귀 모델 훈련

• 특성을 추가한 것뿐, 훈련할 땐 선형회귀랑 동일하게 LinearRegression() 쓰면 됨!
  역시 특성 다양해지니까 선형회귀의 능력이 강해지는구나! 이제 안 찜찜해 ㅎㅎ

2. 특성은 다다익선?

• degree : PolynomialFeatures로 특성 추가할 때, 고차항의 최대차수를 지정하는 매개변수 (기본값 = 2)
  
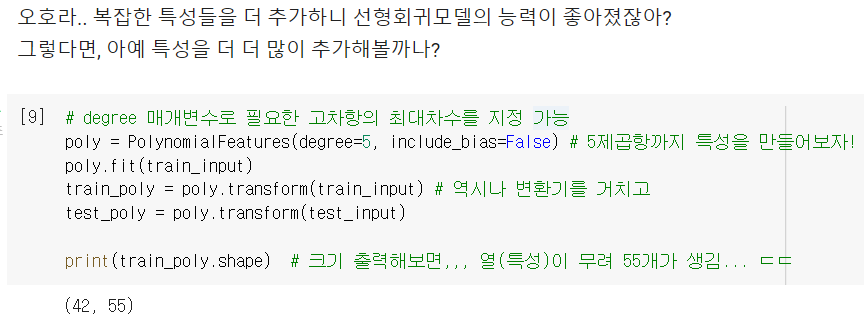
• 많으면 좋을 줄 알고 5제곱항까지 추가해봤는데 ...
  엄청난 과대적합이 되어버렸네 ㅠㅠ

3. 규제

규제(regularization)란?

• 훈련세트에 대한 과대적합을 완화시키는 대표적인 방법.
• 선형회귀의 경우, 계수(기울기)의 크기를 줄여서 보다 보편적인 패턴을 학습하게 함.
  이때, 계수들을 공정하게 줄이기 위해, 스케일 표준화가 필요함!
• StandardScaler() : '표준점수(z)'로 표준화해주는 변환기 클래스
  

릿지 회귀

• Ridge() : 선형회귀에 규제를 추가한 모델. 계수를 제곱한 값을 기준으로 적용하는 L2 규제로, 라쏘보다 릿지를 더 선호하는 경향이 있음.
  
• alpha : 규제의 강도를 조절하는 매개변수로, 값이 커질수록 강도가 세짐.
  ➕ 로그스케일 간격으로 다르게 넣어보면서, 최적의 alpha 값 찾는 게 좋음!
  
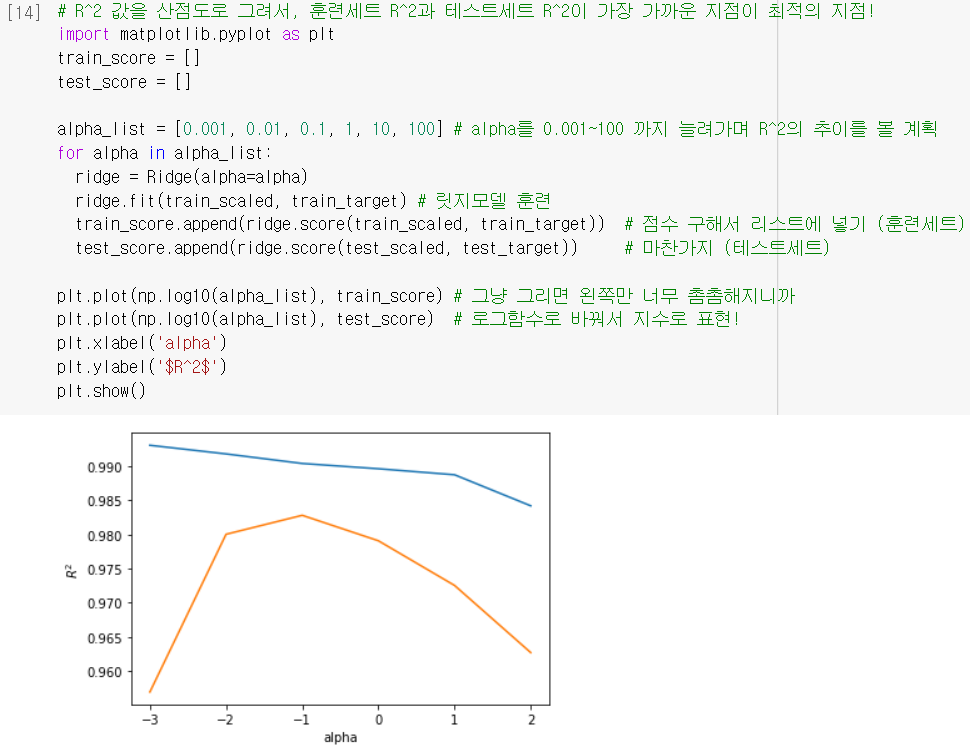
• 찾은 최적의 alpha 값으로 다시 훈련해보면, 확실히 더 좋은 결과!
  

라쏘 회귀

• Lasso() : 선형회귀에 규제를 추가한 모델. 계수의 절댓값을 기준으로 적용하는 L1 규제로, 릿지와 달리 계수를 아예 0으로 만들 수도 있음❗
  
• 마찬가지로 alpha 값을 바꿔가며 규제 강도 조절 가능.
  
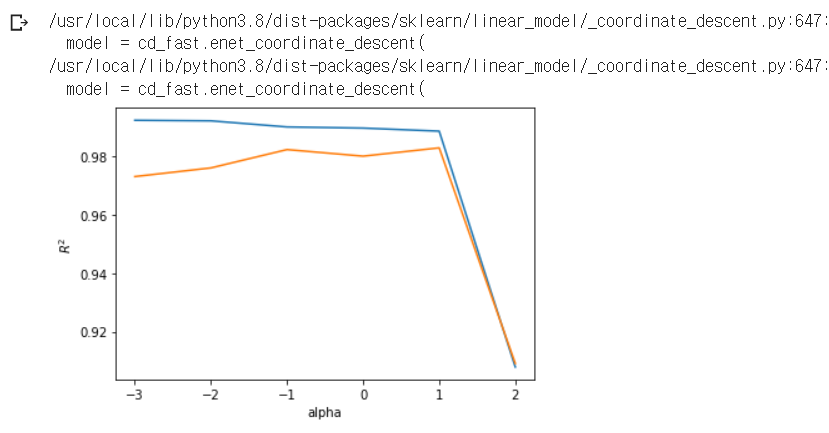
• 역시 최적의 alpha 값으로 다시 훈련해보면, 굿!
  
• ❗ 라쏘는 계수를 아예 0으로도 만들 수 있다던데...
  • np.sum() : 배열을 모두 더한 값을 반환하는 함수. T/F는 1/0으로 인식하여 계산함.
    

= 즉, 40개의 특성은 계수가 0이 되어버렸고, 실질적으로 사용한 계수는 15개뿐이라는 것!

➕플러스 알파

➊ PolynomialFeatures()

• '각 특성을 제곱한 항'과 '각 특성을 서로 곱한 항'을 추가해주는 변환기

poly = PolynomialFeatures()
poly.fit([[2,3]])			# 2,3으로 이루어진 샘플을 변환기에 넣고
print(poly.transform([[2,3]]))  # 변환을 돌리면
---------------------------------------------------------------
[[1. 2. 3. 4. 6. 9.]]			# 이렇게 새로운 특성들 추가됨!

➋ 하이퍼파라미터

• 모델이 학습하는 값(모델 파라미터)가 아니라, 우리가 따로 지정해줘야 하는 값.
• 대표적인 게 위에서 배운 alpha이고, 우리가 했던 것처럼 일일이 설정해보면서 최적의 값을 찾아야 한다. (*이 때, 보통 로그 스케일 간격으로 하는 것이 일반적이다)

---

🤔 Hmmmm...

156p. test_poly 는 왜 .fit() 안 해주나요?

target_poly (훈련세트)로 .fit() 해놨으니 그걸 그대로 쓰는 겁니다! 항상 훈련세트를 기준으로 테스트세트도 변환하는 습관을 들이는 게 좋아요!
🆗= 테스트세트를 따로 .fit()해주는 경우는 없다고 보자!

🤓 To wrap up...

더 높은 결정계수 값을 구하려고 특성의 개수를 늘림 (=다중회귀) → 묻고 더블로 특성공학까지 사용해서 특성을 더 다양하게 늘림 → 결과 굿! → 특성 많을수록 좋아보여서 55개까지 늘려봄 → 심각한 과대적합... → 줄이기 위한 규제 방법 (릿지, 라쏘)을 배움 + 최적의 alpha값 찾기!

오늘은 진짜 새롭게 배운 것들이 꽤 있었다! 앞으로 '과대적합'이 뜨면 릿지 규제, 라쏘 규제가 자연스럽게 떠오르길..!!
(p.171~173 부분 기록 추가하자)