Introduction to Bayesian Statistics(1)

0. Introduction

베이지안 통계(Bayesian Statistics)는 확률이 사건에 대해 특정한 정도의 ‘신뢰’를 제공하는 확률의 베이지안적 해석(Bayesian interpretation)을 기반으로 하는 통계 분야이다. 베이지안적 해석은 고전적인 통계와 관련된 빈도론자(Frequentist)의 해석과는 다른데, 빈도론적 해석은 수많은 시행 끝에 발생하는 상대적인 ‘빈도’를 토대로 확률을 해석하는 반면 베이지안적 해석은 현재 발생한 시행과 사전분포를 이용해 사후분포를 추정하는 등 관점의 차이가 존재한다.
이렇듯 ‘확률’에 대한 베이지안적 해석을 토대로 하는 베이지안 통계는 마르코프 체인 몬테 카를로, 근사적 베이지안 연산, 베이지안 회귀 등의 기법과 베이지안 딥러닝, 베이지안 메타러닝 등의 분야에 널리 쓰이고 있다. 특히, 전 세계에 인공지능의 부흥을 불러 일으킨 구글 딥 마인드의 바둑 인공지능 ‘AlphaGo’ 또한 딥러닝 모델과 함께 베이지안 기반 기법 중 Monte Carlo Tree Search를 사용해 인공지능의 괄목할 만한 성능 향상을 보여주기도 했다.

1. Basic of Probability

1.1 확률변수란?

쉽게 말하면, 일반적으로 자주 쓰이는 확률변수(X)는 사건이 존재하는 표본공간(S)에서 실수(R)로 대응하는 함수로 정의된다.

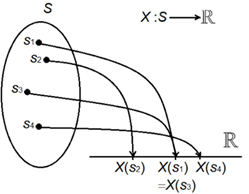
이 때, 확률(P)은 사건이 존재하는 표본공간(S; sample space)에서만 정의되기 때문에 아래와 같은 식으로 확률변수에 대한 확률을 정의할 수 있다.

$𝐴⊂ℝ~인 ~~𝐴에~~ 대해,$
$𝑃(𝑋∈𝐴)=𝑃(𝑋^{−1}(𝐴))=𝑃({𝑠∈𝑆:𝑋(𝑠)∈𝐴})$

즉, 확률변수는 정의역이 표본공간이고 공역이 실수인 함수이며, 공역의 종류에 따라 이산확률변수 또는 연속확률변수로 나뉜다.

이산확률변수

• 확률변수에서 공역이 셀 수 있는(countable) 집합인 경우
  Ex) 동전의 앞/뒤, 교통사고 건수, 성공 횟수 등

예를 들어, 확률변수 $X$가 서울 시내에서 발생하는 하루에 교통사고 건수를 나타낸다고 가정해보자. 이 때 $X$는 이산형 분포인 포아송 분포를 따른다고 가정할 수 있다.

$X$ ~ $Poi(5),$
$X∈\{0,1,2,3,…,∞\}$

연속확률변수

• 확률변수에서 공역이 (실수에서) 일정 구간의 모든 값을 가질 수 있는 경우
  Ex) A공장에서 생산한 전구의 사용 기간, 키, 몸무게 등

예를 들어, 확률변수 X가 한국 남자의 키를 나타낸다고 가정해보자. 이 때는 X가 정규분포를 따른다고 가정할 수 있다.

$X$ ~ $N(μ=174,σ^2=5^2),$
$X∈\{159.2,163.4,168,172.5,173,174.5,176.8,183,224\}$

1.2 베이즈 정리

조건부 확률

두 사건 A,B에 대해 사건 B가 이미 일어났을 경우, 사건 A가 일어날 조건부 확률은 아래와 같이 정의된다.

$P(A│B)=$ $P(A∩B)\over P(B)$

확률의 곱법칙

조건부 확률의 정의를 이용하면 아래와 같이 성립함을 쉽게 확인할 수 있다.

$P(A∩B)=P(B)P(A│B)=P(A)P(B|A)$

표본공간의 분할

k개의 사건들의 집합인 $\{A_1,…,A_k\}$가 다음의 두 성질을 만족할 때 $\{A_1,…,A_k\}$가 표본공간 $S$의 분할(partition)이라 한다.

1. $A_1,…,A_k$가 서로 배반
2. $P(\cup_{i=1}^k A_i )=1$

베이즈 정리

기본적으로 가능한 사건들({A_1,…,A_k})가 분할일 때, 조건부 확률의 정의와 확률의 곱법칙을 이용하면 베이즈 정리가 성립함을 알 수 있다.

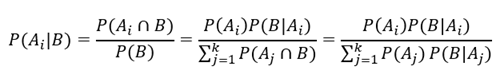
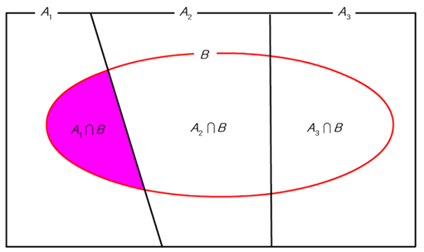
(베이즈 정리를 한 눈에 나타낸 그림)

베이즈 정리의 예로, 고등학교 수학 과정인 확률과 통계에서 자주 나오는 문제를 들 수 있을 것 같다.

문제

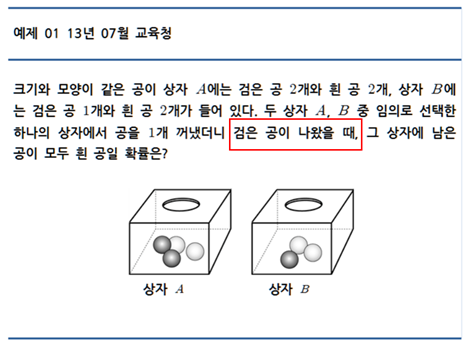
풀이

위의 베이즈 정리는 기본적으로 사건의 관점에서 서술된 식이다. 이 때, 매개변수 θ를 추론하는 데 데이터 X를 이용하는 통계적 추론을 생각해보자. 그러면 위 식을 아래의 식으로 간단하게 나타낼 수 있다.

1.3. Posterior -> prior + likelihood

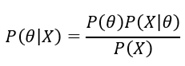
즉, ‘데이터 X가 주어졌을 때 매개변수 θ를 추정하는 문제(P(θ|X))’와 같은 어려운 task를 ‘매개변수 θ가 주어졌을 때 데이터 X의 분포를 활용(P(X|θ))’하는 상대적으로 쉬운 task를 통해 해결할 수 있는 것이다.
이 때, P(θ|X)는 데이터가 주어진 이후의 θ의 분포를 뜻하는 사후 분포(posterior), P(θ)는 데이터가 주어지기 이전의 θ의 분포를 뜻하는 사전분포(prior), $p(X|\theta)$는 관측(observation(likelihood))라고 한다.

2. Classical Statistics vs Bayesian Statistics

베이지안 통계(Bayesian Statistics)는 기존의 고전적인 통계(Classical Statistics)의 몇 몇 문제(?)를 해결하기 위해서, 또는 통계적 추론에 있어서 고전적인 통계를 사용하는 빈도 확률론자(frequentist)의 관점에서 벗어나 다른 태도를 취하기 위해 생겨난 철학으로 여길 수 있을 것 같다. 고전적인 통계는 물론이고 베이지안 통계 또한 베이지안 통계추론, 베이지안 딥러닝, 베이지안 메타러닝, 베이지안 최적화 등 수 많은 세부 분야들이 존재하기에 고전 통계와 베이지안 통계를 명확히 구분 지을 수는 없지만, 본 글에서는 아래와 같은 특성들을 기반으로 둘을 나눠보려 한다.

고전적 통계: 결정적, 상수, 확실성, 많은 데이터, 이론적, 전수조사
베이지안 통계: 비결정적, 변수, 불확실성, 적은 데이터, 근사적, 샘플링, 신뢰도

위와 같은 특성들을 기반으로 베이지안 통계(Bayesian Statistics)가 기존의 고전적인 통계(Classical Statistics)와 어떤 차이점이 있는 지 다양한 예시를 들어 살펴보도록 하자.

2.1 고전적 추론 vs 베이지안 추론

통계추론의 핵심 중 하나는 주어진 데이터($X$: 확률변수, $x$: 관측치)를 이용하여 미지의 관심 모수 $θ$를 추정하는 것이다. $f(X|θ)$를 미지의 관심 모수 $θ$에 의존하는 확률변수 $X$의 분포의 밀도 함수라 가정하자.

고전적 추론 – MLE

고전적 추정의 대표적인 방법 중에는 최대 우도 추정(Maximum Likelihood Estimation; MLE)가 있다. 데이터($x$)가 주어진 경우 매개변수($θ$)의 가능도를 나타낸 가능도 함수 $L(θ|x)$는 아래와 같이 정의된다. 가능도 함수는 일종의 사후분포라 할 수 있다.

$L(θ│x)$=$f(x|θ)$

즉, 데이터 $X$가 $θ$에 대한 정보를 가지고 있을 것이기에, 데이터 $X$를 통해 매개변수 $θ$를 추측하는 것이다. 단, 이 때 $θ$가 $X$의 분포를 결정하지, $X$가 $θ$의 분포를 결정하는 것은 아니다. 이 때 최적의 매개변수를 뜻하는 최대 우도 추정량($\hat\theta$)은 아래와 같이 정의한다.

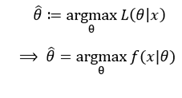
베이지안 추론 – prior distribution

이에 대응하는 베이지안 추론은 큰 틀은 비슷하지만, 베이즈 정리를 이용한다는 점에서 큰 차이가 있다.

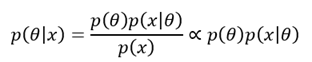
즉, 관측치 $x$가 주어진 이후 매개변수 $θ$의 확률 분포인 $p(θ|x)$, 즉 사후분포(posterior)를 얻기 위해 사전분포(prior)인 $p(θ)$와 자료(likelihood) $p(x|θ)$를 모두 활용하는 것이다.

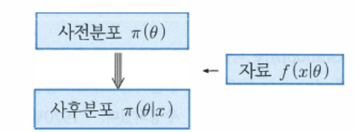
(베이지안 추론의 개념도)

2.2 신뢰 구간 vs 신용 구간

고전적 추론 – 신뢰구간(Confidence Interval)

고등학교 확률과 통계에 나온 신뢰구간이 여기서의 Confidence Interval에 해당한다. 추론하고자 하는 $θ$의 $100(1-α)\%$ 신뢰도를 갖는 신뢰구간은 아래와 같은 방식으로 정의된다.

$P[L(X)<θ<U(X)│ θ]=1-α$

즉, 특정 $θ$를 추정하기 위해, $θ$를 상수로 가정한 후 신뢰도 $100(1-α)\%$를 갖는 신뢰 구간을 정의한다. 그 후, 데이터가 $x$로 관측됐을 때 위 식에 ‘대입’하여 관측 값에 대한 신뢰구간을 사용한다. 예를 들어, 95%의 신뢰도로 매개변수 $θ$(여기서는 모평균 $μ$)를 추정한다고 가정해보자. 이 때 신뢰구간은 아래 그림과 같은 의미를 가진다.

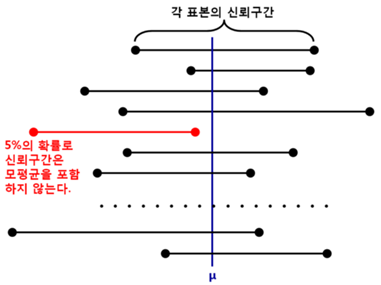
위의 그림은 95%의 신뢰도로 $θ$를 추정한다는 것은 $θ$가 해당 신뢰구간에 포함될 확률이 95%라는 것이 아니라, $θ$를 포함하는 신뢰구간이 약 100개 중 95개에 해당할 것이라는 사실을 보여준다. 즉, 신뢰 구간은 데이터가 $X=x$로 관측될 때, $θ$가 해당 신뢰구간에 포함될 확률은 아래와 같이 이산적으로 나타난다.

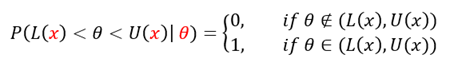
고전적 추론의 관점에서는 $θ$를 추정하는 데 $θ$를 이미 상수로 가정하고 신뢰구간을 구한 다음, 관측치 $x$를 대입함으로써 신뢰구간을 구하기 때문에 $θ$ 추론에 있어서 직관적이지 못한 것을 알 수 있다.

베이지안 추론 – 신용구간(Credible Interval)

베이지안 추론에서의 신용구간은 위와 같이 추정하고자 할 $θ$를 상수로 가정하지 않고 확률변수로 가정한다. 이를 토대로 데이터 $X=x$가 관측됐을 때, $100(1-α)\%$ 신뢰구간은 아래와 같이 정의된다.

$P(L(x)<θ<U(x)| x)=1-α$

이를 통해, θ가 구간 (L(x),U(x))에 놓일 확률은 정확히 1-α가 된다.

다시 신뢰구간과 신용구간을 비교하면 아래와 같다.

신뢰구간

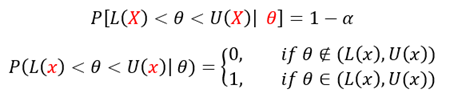
신용구간

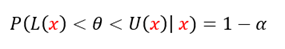
즉, 고전적 추론에서 편이, 분산, 신뢰구간, 가설검정 등의 오차확률은 모든 가능한 X값에 대하여 적분, 합 등의 형식을 취한다. 그렇기 때문에 위의 신뢰구간도 현재 주어진 관측치가 아닌 표본조사를 무한히 반복했을 때 발생할 모든 관측치들을 고려해서 얻어진 것이다. 베이지안 통계추론은 단순히 현재 주어진 관측치에만 의존하기 때문에 빈도론자들의 통계추론(고전적 통계추론)과는 관점이 다른 것을 알 수 있다.

2.3 Simulated Annealing vs Markov Chain Monte Carlo

담금질 기법(SA; Simulated Annealing Method)과 마르코프 체인 몬테 카를로(MCMC; Markov Chain Monte Carlo Method)은 특정 model의 매개변수 벡터 θ를 추정하기 위한 최적화(Optimization) 기법들이다. 이를 고전적 추론과 베이지안 추론을 구분 짓는 잣대를 위한 예시로 사용한 이유는 담금질 기법은 매개변수 θ를 결정적으로 추정하고 몬테 카를로 마르코프 체인은 매개변수 θ를 비결정적으로 추정하는 데에 있다.
이를 위해 담금질 기법을 사용해 매개변수를 추정했던 본인의 연구를 예시로 들어보자.

해당 연구에서는 한국 내의 코로나19 감염병의 전파를 기술하기 위해 아래와 같은 모델을 정의한 후, 2020년의 보건 복지부 데이터(신규 확진자, 격리자, 회복자, 격리 기간, 무증상 확진율 등)을 이용해 매개변수를 추정(최적화)하는 과정이 포함되어 있다.

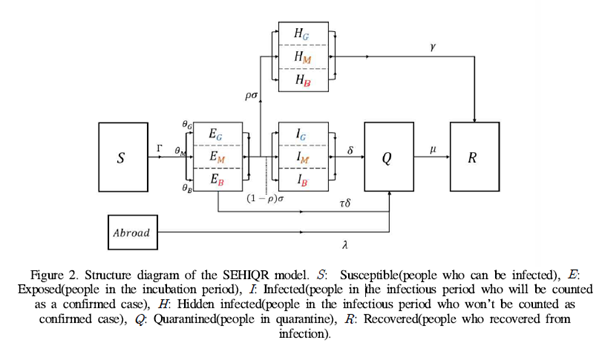
(감염병 전파를 위한 모델)
위 그림에 나타나 있는 매개변수들은 예측 확진자와 실제 확진자의 차이(MSE)를 줄이는 방향으로 최적화된다.

2.3.1 담금질 기법(Simulated Annealing)을 이용한 최적화

담금질 기법은 실제 금속공학에서 쓰이는 담금질에서 모티브를 얻어 최적화 문제에 적용된 기법이며, 실제로는 아래와 같이 매우 어려운 조합 문제인 Travelling salesman problem을 해결하기 위해 도입된 것으로 알려졌다.

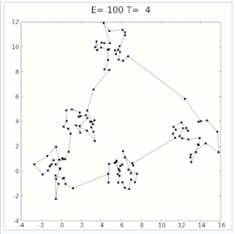
https://en.wikipedia.org/wiki/File:Travelling_salesman_problem_solved_with_simulated_annealing.gif

이런 조합에 관한 문제 외에도 연속적인 매개변수를 추정하기 위해 쓰이기도 한다.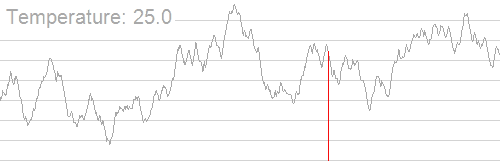

https://en.wikipedia.org/wiki/File:Hill_Climbing_with_Simulated_Annealing.gif

한 마디로, 온도가 높을 때에는 매개변수 공간(parameter space)를 넓은 보폭으로 전역적으로 탐색해 전역 최적점을 근사적으로 살펴본 다음, 온도가 낮아짐에 따라 좁은 보폭으로 지역적인 최적점을 향해 나아가는 방법이다.

(코로나19 연구에 사용된 담금질 기법 기반 알고리즘)

Parameter 추정 결과
이 기법을 통해서 추정된 모든 매개변수들은 결정적으로(즉, 상수로) 정해진다.

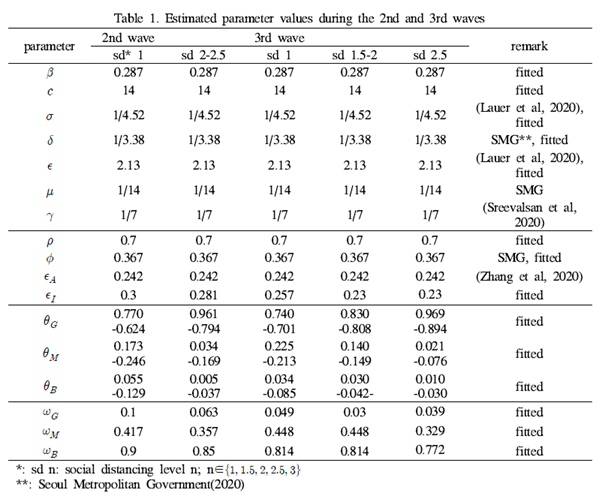
즉, 담금질 기법은 어느 정도 주어진 problem에 대해 매개변수 벡터인 θ에 대한 근사적인 전역 최적 값(Global optim)을 제공한다. 하지만 이 방법 또한 근사적인 방법이기 때문에 전역 최적 값이라는 보장은 없으며, 매개변수가 많아짐에 따라 전역 최적 값에 근사하는 매개변수 조합이 많아 지기 때문에 추정된 매개변수가 진정 옳은 지에 대한 통찰은 주지 못한다. 즉, 추정된 매개변수의 신뢰도와 관련해서는 어떠한 정보도 주지 못하는 것이다. 그렇기에 다른 방법을 활용해 매개변수의 신뢰도를 제고할 필요성이 있다.

2.3.2 마르코프 체인 몬테 카를로(MCMC)를 이용한 최적화

기본적으로 매개변수 추정과 관련해 현존하는 연구들은 상당히 많은 수가 (베이지안적 관점의) MCMC 기법을 사용하며, 쓰이는 알고리즘이 변형되더라도 기존의 큰 틀은 벗어나지 않는다.

(상당히 많은 수의 연구가 MCMC 기반 기법들을 사용한다.)

몬테 카를로와 관련해서는 후술하기로 하고, MCMC 기법의 결과에 대해서만 간단히 알아보자.

(위키디피아에서의 MCMC)

MCMC는 간단히 말하면 샘플링을 통해 구하고자 하는 매개변수의 분포를 모사하는 기법이다.

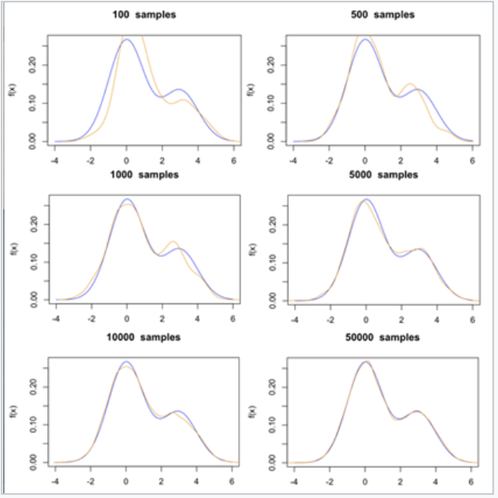
(샘플이 많아짐에 따라 목표 매개변수(파란 선)의 분포를 모사하는 모습)

MCMC기법을 활용해서 매개변수 θ의 분포를 추정한다면 해당 매개변수가 비결정적으로 정해지며, 신용구간 또한 구할 수 있는 장점이 존재한다. 이 장점으로 인해 매개변수를 추정(최적화)하는 대부분의 연구에서는 매개변수의 최적 값 외에도 95% C.I(Credible Interval)을 포함하는 것으로 보인다.

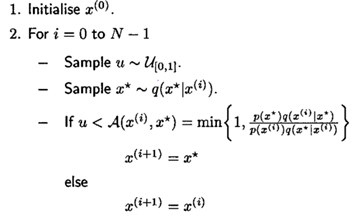
(MCMC 알고리즘 중 대표격인 MH(Metropolis-Hastings) 알고리즘)

Parameter 추정 결과
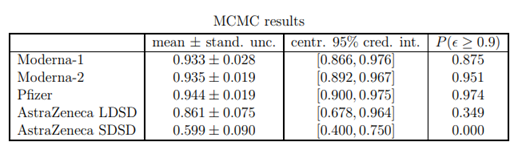(MCMC기법은 최적 값 뿐만 아니라 95%의 신용구간 또한 구할 수 있다.)

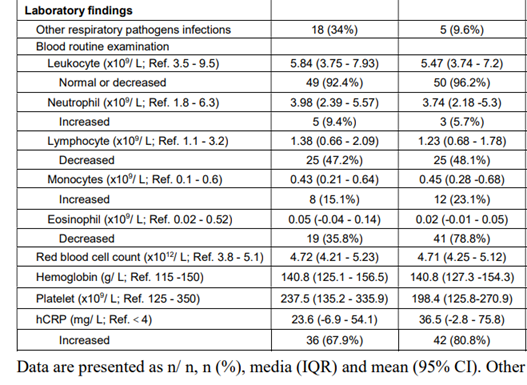
(MCMC기법이 아니여도 보통 특정한 수치를 추정할 때에는 95% CI를 포함한다.)

2.3.3 문제 예측 - 결정적 최적화 vs 비결정적 최적화

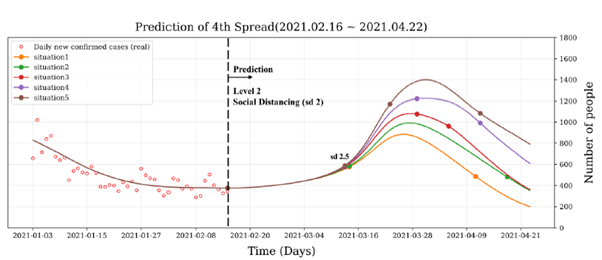
(담금질 기법의 결정적인 매개변수의 경우)

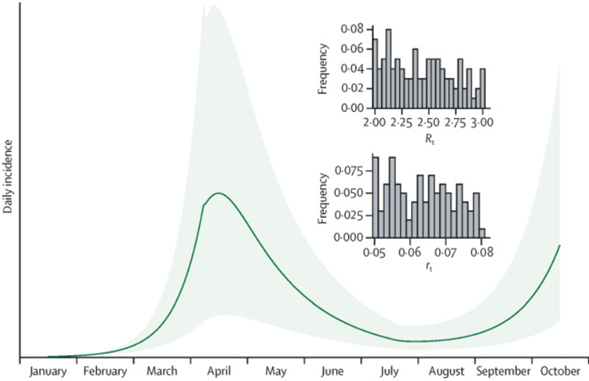
(MCMC 관련 기법의 비결정적인 매개변수의 경우)
위 그림의 차이와 같이, 매개변수가 결정적으로 정해진다면(즉, 상수로 여겨진다면) 목표 통계량(여기서는 신규 확진자)에 대해 (다양한 상황을 가정하지 않는 한) 하나의 결과만을 나타낼 수 있지만 매개변수 비결정적으로 정해진다면(즉, 분포로 여겨진다면) 같은 통계량에 대해서 95% 신용 ‘구간’을 나타낼 수 있게 된다. 이처럼 베이지안 기반 통계는 매개변수나 통계량 자체에 ‘신뢰도’, 혹은 ‘오차’ 등에 대한 정보를 제공함으로써 보다 풍부한 추론을 가능케 한다.

Introduction to Bayesian Statistics(2)

Continue on new post... - Introduction to Bayesian Statistics(2)

Ref

Predictability of case evolution of COVID-19 using MCMC | by Thomas Vergote | Medium
What is the probability that a vaccinated person is
shielded from Covid-19?
Simulated annealing - Wikipedia
Markov chain Monte Carlo - Wikipedia
모평균의 구간추정 예시 : 네이버 블로그
베이지안 통계학,서울시립대학교 통계학과 전공 수업(2021).