Introduction to Bayesian Statistics(2)

3. 베이지안+ 딥러닝 + 강화학습 = AlphaGo

3.1 몬테카를로

몬테카를로(Monte-Carlo)는 도시국가인 모나코 북부에 있는 지역으로 카지노, 도박으로 유명한 곳이다. 수학의 확률이론 자체가 도박에서 비롯되었기에 도박 도시의 대명사였던 몬테카를로 역시 확률론과 밀접한 관계가 있는 방법론을 지칭하기도 한다.
즉, 몬테카를로 방법이란 무작위 추출된 난수를 이용해 함수의 값을 계산하는 통계학적 방법으로, 수치적분이나 최적화 등에 널리 쓰인다.

적분 문제 중 면적 계산을 예로 들어보자. 위 그림에서 검은 실선에 의해 구분되는 파란색 영역의 넓이를 구하고자 할 때, 함수로 표현하기 힘들거나 이론적인 적분 값을 구하기 힘든 경우 몬테카를로 기법을 사용할 수 있다. 이 때, 정사각형으로 이루어진 영역의 상태 공간에서 임의로 샘플(데이터)을 뽑는다. 정사각형의 넓이는 알고 있기 때문에 정사각형 내부의 총 샘플 수와 파란색 영역에 속하는 샘플 수의 비율을 이용하면 파란색 영역의 넓이 또한 근사적으로 알 수 있게 된다.
오늘날 인터넷 상에는 적분 계산기(Wolfram Alpha 등)가 많이 존재하므로 특정 방정식에 대해 이론적인 면적을 계산하지 못하는 경우가 많지는 않다. 하지만 특정 영역에서는 이론적인 적분을 하지 못하는 경우가 존재하며, 가능하더라도 실행의 용이성 및 연산의 효율성 등의 이유로 몬테카를로 샘플링을 주로 이용하곤 한다.
베이지안 통계 추론에서는 가령 데이터가 주어졌을 때 사후 분포를 구하고, 이로부터 사후 평균이나 분산 등을 구하고자 할 수 있다. 이 경우 평균, 분산과 같은 통계량을 수리적으로 구하기는 어렵지만 사후 분포로부터 표본을 생성할 수 있는 경우가 종종 발생한다.
즉, 아래와 같은 적분 값
$I=∫_a^bg(x)f(x)dx$ 을 구하기 힘들 때,
$f(x)$ 라는 밀도 함수로부터 여러 개의 샘플($x$)을 얻을 수 있다고 가정해보자
이 때 확률에서 기댓값의 정의에 따라 $I=E(g(x))$ 로 나타낼 수 있다.
즉, $f(x)$로 부터 샘플 $x$를 많이 얻을 수 있다면, 위의 적분 값(또는 이론적 기댓값)은 아래와 같이 n개의 샘플 $x_1,x_2,….x_n$을 통해 근사적으로 구할 수 있게 된다.

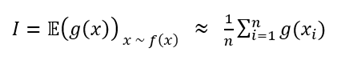
이처럼 샘플(난수)의 개수를 더욱 많이 발생시킬수록 더욱 정확한 값을 얻을 수 있겠지만, 확률적인 방법론이기 때문에 어느 정도 오차가 발생할 수밖에 없다.
다양한 컴퓨터 시뮬레이션, 예측 등에 쓰이지만 역사적으로 가장 중요한 사례로 미국의 원자폭탄 개발 계획인 ‘맨해튼 프로젝트’를 들 수 있다.

폴란드 출신의 수학자 스태니슬로 울람은 그 유명한 폰 노이만과 함께 맨해튼 프로젝트에 참가하였다. 울람은 새로운 수학적 방법론을 도박의 도시 이름을 따서 몬테카를로 방법이라 명명하였고, 이 방법은 중성자가 원자핵과 충돌하는 과정을 이해하고 묘사하는 데 결정적 역할을 하였다.
즉, 핵분열의 과정에서 우라늄 원자핵과 충돌한 중성자 1개가 다시 중성자 3개를 방출하는데, 이 연쇄반응에서 중성자들은 마치 분기하는 나뭇가지들처럼 복잡한 경로를 보인다. 몬테카를로 방법을 적용한 확률적 시뮬레이션을 통해 이 경로를 파악하고 결과를 ‘추정’할 수 있는 것이다.

3.2 알파고

알파고를 개발한 구글의 딥마인드는 <딥러닝 신경망과 트리 검색으로 바둑 마스터하기(Mastering the game of Go with deep neural networks and tree search)>라는 제목으로 네이처 논문에 알파고의 기반 기술과 알고리즘을 자세히 설명해 놓았다. CPU 1,202개, GPU 176개 등 분산 컴퓨터, 정책망 및 가치망으로 이루어진 신경망, 과적합 방지를 위한 지도학습과 강화학습의 결합, 고속 시뮬레이션, 롤아웃 등 중요한 요소 또한 존재하지만 여기서는 핵심적인 알고리즘인 몬테카를로 트리 서치의 기본 구조만을 나타내었다.

몬테카를로 트리 서치

바둑은 가로세로 19줄로 이루어진 바둑판 위에 흑돌과 백돌이 서로의 집을 만들고 세력 다툼을 하는 개념의 게임이다. 숫자로 계산해보면 바둑에서 착수가 가능한 모든 패턴은 약 10^171 가지로, 우주의 모든 원자 개수인 약 10^81보다도 훨씬 많다. 그렇기에 컴퓨터의 연산 능력이 아무리 좋아져도 바둑은 절대 인간을 이길 수 없다는 의견이 지배적이었는데, 알파고 기반 인공지능은 어떻게 인간을 압도하는 성능을 가지게 됐을까?

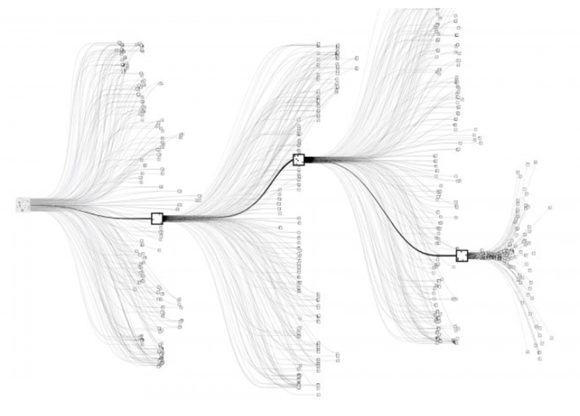
몬테카를로 트리 서치는 Min-max 알고리즘의 성능을 개선한 알고리즘으로, 모든 경로를 탐색하기 불가능한 상황에서 효율적이다. 간단히 말해 ‘경우의 수가 너무나도 많을 때 순차적으로 시도하는 것이 아닌 랜덤하게 시도하는 것’ 이다.

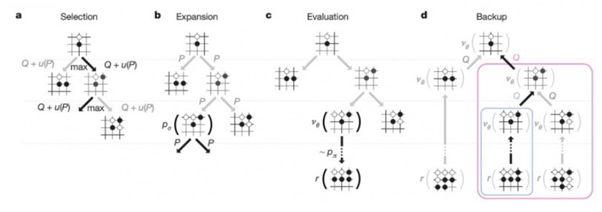
바둑은 착수 후 상대방이 어디에 둘 것인지, 또 그 다음 수는 어디에 둬야할 지 계속해서 선택과 경우의 수가 굉장히 많이 발생한다. 그렇기 때문에 무작위로 일정 횟수만큼 착수를 한 다음, 그 중 가장 승률이 높은 수를 두게 되는 것이다. 이를 위해 고속 시뮬레이션, 롤아웃, 분산 컴퓨팅 등 다양한 보조 기법들이 사용되었다.

4. 베이지안 딥러닝 / 메타러닝

4.1 베이지안 뉴럴 네트워크(BNN)

기존의 뉴럴 네트워크는 뉴런들 사이에 존재하는 layer들의 parameter가 상수로 부여되는 반면, 베이지안 뉴럴 네트워크는 그 parameter 자체를 하나의 분포로 생각한다. 즉,학습을 할 때에는 parameter의 확률 분포에 해당하는 모수(예를 들어 정규분포에서는 평균과 분산)를 학습하고, 예측을 할 때에는 그 분포로부터 샘플링을 통해 얻음으로써 95% 신뢰도를 부여한 불확실한 예측을 하는 것이 베이지안 뉴럴 네트워크의 특징이다.
즉, 불확실성(Uncertaintiy)를 다루기 위해 ‘모르는 건 모른다고 하는 모델’을 만드는 것이다. 가령, 이미지 분류 모델에서 개와 고양이를 대상으로 학습을 시킨 다음, 자동차를 분류 예측에 사용한다면 자동차 이미지는 개 또는 고양이에 해당하는 결과를 낼 것이다. 베이지안 뉴럴 네트워크는 이처럼 어떻게든 결과를 내는 것이 아니라, 만약 자동차 이미지의 분류 결과가 고양이일 확률 40%, 강아지일 확률 60%의 분포를 갖는다면, 모델로 하여금 ‘모르겠다’ 라는 반환 값을 내놓게끔 설계된 것이다.
이러한 불확실성은 신뢰도가 필요한 분야(의학, 자율주행) 등에서 활용될 수 있다. 예를 들어 운전을 할 경우에는 언제 어떤 사고가 일어날 지 모르기 때문에 초록 불이라 해서 그냥 속도를 계속 내서는 안 된다. 차가 갑자기 들어올 수도, 갑자기 빨간 불이 될 수도 있기 때문에 항상 불확실성을 염두에 두고 판단을 내려야 하는 것이다.

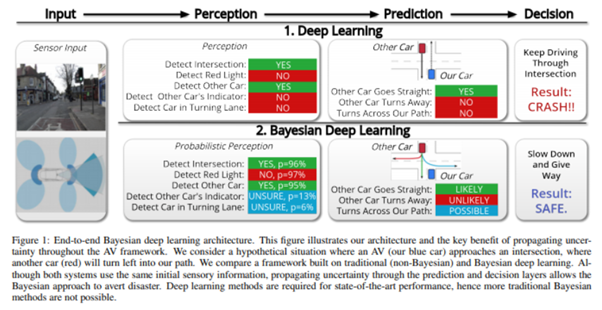
이러한 BNN과 유사한 역할을 수행할 수 있는 것이 흔히 알려진 Dropout이다. 가령, Dropout을 학습 때만 적용하고 Evaluation 단계에서는 사용하지 않는 것이 보통이지만, Evaluation 때에도 dropout을 사용한다면 시행마다 결과가 조금씩 다를 것이고, 이로부터 불확실성(Uncertainty)를 추정할 수 있게 된다(Monte Carlo Dropout 등).
베이지안 딥러닝(베이지안 뉴럴 네트워크)가 보여준 것처럼 인공지능 모델의 블랙박스 특성에 대해 고찰하고, 신뢰도 등을 제고하려는 노력은 이 네트워크가 큰 그림에서 볼 때 XAI(eXplainable AI, 설명가능한 인공지능)에 속할 수 있다는 것을 암시한다.
국내 인공지능 솔루션 스타트업 중 하나인 에이아이트릭스(AITRICS) 또한 인공지능의 해석 가능성을 높이기 위해 ‘해석 모듈(Interpretation module)’과 결과에 대한 불확실성을 계산하여 신뢰도를 제공하는 ‘베이지안 뉴럴 워크(Bayesian neural networks)’ 기술을 도입했다고 한다.

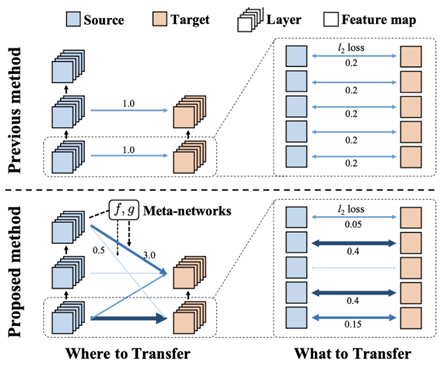
(에이아이트릭스 메타트랜스퍼(AITRICS metatransfer) 방법, 메타 네트워크 f와 g는 채널의 중요도에 따라 두 네트워크의 레이어 사이에 전달할 지식의 양을 결정한다.)
이에 추가로 베이지안 뉴럴 네트워크와 시계열 모델(attention)을 결합해 시계열 데이터에서 불확실성을 고려한 의사 결정을 할 수 있는 ‘Uncertainty-awre attention mechasim’, 전이 학습(transfer learning)의 전이 방식이 해석하기 까다롭다는 문제를 해결하기 위해 ‘meta learning method’ 등을 제안하였다. 메타러닝 방법론을 이용해 특정 task를 해결하기 위해 어떠한 task에서 얼마만큼의 지식을 끌어와야 하는지, 또 그런 지식들이 현재 문제를 풀기위한 딥 네트워크의 어떠한 파라미터를 최적화하는 데 주로 사용되어야 하는지를 학습하는 방법론으로, 결과의 근거를 유추하여 해석을 가능하게 하며 전이 학습의 효율성을 증대시켜, 예측 성능을 큰 폭으로 향상시킬 수 있다고 한다.

4.2 Meta-Learning is All You Need

메타러닝의 전반적인 지식과 블랙박스 메타러닝, 최적화 기반 메타러닝, 비모수(Non-parametric) 메타러닝 등을 살펴본 논문으로, 여기서도 베이지안 기반 메타러닝에 관한 내용이 소개되었다.

(메타러닝 문제는 대략적으로 결정적 관점과 확률적 관점 두 가지로 나뉜다.)

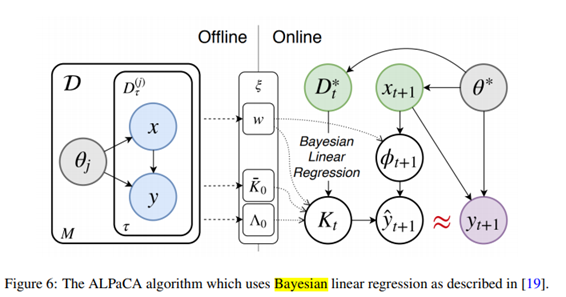
(베이지안 선형 회귀를 사용한 ALPaCA 알고리즘)

특히, 저자는 글의 마지막에도 메타러닝에는 베이지안 메타러닝과 메타 강화학습 등과 같은 흥미로운 분야가 많다고 얘기하며, 메타러닝을 사용해 헬스케어나 제조업 등 다양한 실생활 분야에 적용하기를 기대한다며 논문을 끝마치기도 한다.

이처럼 베이지안 관련 통계 기법들은 반 세기 전 원자폭탄부터, 최근 인공지능 분야까지 폭 넓게 쓰이고 있다. 앞으로 더욱 완벽한 인간 중심 인공지능을 개발하기 위해 설명 가능 인공지능, 강화 학습 등이 끊임 없이 발전하고 있는 상황에서 베이지안-식 관점을 가지고 문제를 바라본다면 이전 보다 흥미로운 접근이 가능할 것이라고 생각한다.

Ref(2)

머신러닝 메타러닝(Learning To Learn) (tistory.com)
베이지안 메타 학습 만 있으면됩니다 (ichi.pro)
최근 머신 러닝 핫한 연구 분야 (1/3) :: 취미생활하는 공대생 (tistory.com)
닥터박 :: 알파고, 몬테카를로 트리탐색 (tistory.com)
몬테카를로 방법과 인공지능 – Sciencetimes