기본 레이어 이해하기 시리즈
Convolution == 만능?
Convolution Layer의 장점을 생각해보자. Linear Layer 대비 효율적인 연산 과정, 약간의 데이터 소실에도 불구하고 (특히 이미지 처리 과정에서) low-level부터 high-level까지 다양한 지역적 특성을 비교적 수월하게 추출할 수 있다는 점 등을 꼽을 수 있겠다.
장점만 놓고 보면 마치 만능처럼 보인다. 하지만 합성곱 레이어에는 큰 단점이 한 가지 있는데, 바로 한정된 크기의 필터로만 데이터를 읽어온다는 점이다. 그런데 이게 왜 문제일까?
한 번 지정된 필터 크기만큼씩만 데이터를 읽을 경우 발생할 수 있는 문제점을 생각해보자.
크게 다음의 두 가지를 꼽을 수 있다.
What if...
1. 구분하고자 하는 패턴이 지정한 필터 크기보다 클 경우
2. 구분하고자 하는 패턴이 필터 경계선에 겹치는 경우
두 문제 모두 필터의 크기를 늘리면 해결할 수 있을 것처럼 보인다. 하지만 그 경우 필터의 크기를 얼마나 늘려야 하는가에 대한 문제가 발생한다. 극단적으로는 필터 크기가 이미지의 크기와 같아질 수도 있겠지만, 이 경우 합성곱 레이어는 선형변환 레이어와 똑같은 일을 하게 된다. 결국 필터의 크기를 늘리는 것은 근본적인 해결책이 아니다.
Receptive Field
필터의 크기를 늘릴 수 없다면, Receptive Field 를 늘리면 된다. 수용 영역 이라고도 번역되는데, 쉽게 말해서 필터를 통해서 보는 영역을 가리킨다. (합성곱 레이어 파트에서 살펴봤던 윈도우 개념과 똑같은 것처럼 느껴질 수도 있지만 둘은 엄연히 다른 개념이다.)
그런데 필터 대신 수용 영역을 늘리면 된다는 말은 마치 모순처럼 들린다. 앞에서 분명히 필터의 크기를 늘리는 것은 근본적인 해결책이 아니라고 했는데, 필터를 통해서 보는 영역의 크기를 늘리면 해결할 수 있다? 어떻게 이게 가능할까?
나무 말고 숲을 보자
한 개의 필터를 나무, receptive field를 숲으로 생각해보자. 여러 개의 필터가 보는 윈도우를 하나의 수용 영역으로 묶을 수 있다면 수용 영역이 커지는 것과 같은 효과를 낼 수 있을 것이다.
어떻게 하면 여러 개의 윈도우를 하나로 묶어 계산할 수 있을까?
정답은 윈도우를 통해 생성된 feature map 여러 개를 동시에 계산하는 것이다. 동시라고 하니까 어려워 보이지만, 예시를 통해 살펴보면 쉽게 이해할 수 있다.
Pooling == 피처 맵의 피처 맵
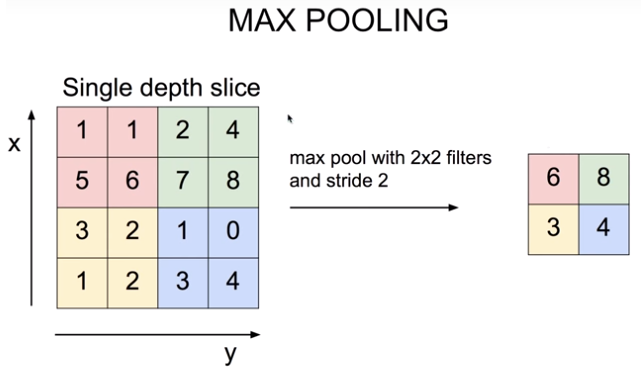
위 그림에서 왼쪽 사각형은 합성곱 연산을 통해 추출된 feature map이고, 오른쪽 사각형은 왼쪽의 feature map의 색칠된 구역별로 가장 큰 값을 추출한 것이다. feature map의 feature map이라고도 할 수 있다.
이게 바로 Pooling Layer에서 하는 일이다.
풀링 레이어는 쉽게 말해서 피처 맵들의 피처 맵을 만드는 작업이다. 앞서 합성곱 레이어에서 피처 맵을 만들 때 필터와 스트라이드를 사용한 것처럼 풀링 레이어에도 필터와 스트라이드 개념이 존재한다. (위 그림에서 풀링 레이어의 필터 크기는 2*2이고, 스트라이드는 2이다.)
결과적으로 우리는 풀링 레이어에서 추출된 피처 맵만 보고도 어떤 패턴이 어떤 지역에 있는지 알 수 있다. 또한 연산 측면에서도 이득을 볼 수 있다. 풀링 과정에는 별도의 파라미터나 복잡한 연산이 필요하지 않기 때문이다.
여러가지 풀링 방법
위 그림처럼 최대값을 추출하는 것을 Max Pooling, 최소값을 추출하는 것을 Min Pooling, 각 값의 평균을 내어 추출하는 것을 Mean Pooling이라고 한다.
CNN 등 이미지 처리 네트워크에서는 주로 Max Pooling을 사용한다. 최대값 풀링은 합성곱 연산으로 추출된 각 지역별 피처의 특성을 강조하는 효과가 있기 때문이다.
물론 굳이 풀링을 쓰지 않고 여러 겹의 Convolution Layer를 쌓을 수도 있다. 하지만 합성곱만으로 수용 영역을 크게 만드려면 아주 많은 양의 레이어가 필요하다. 결과적으로 연산 효율 측면에서 오히려 손해일 뿐만 아니라 Overfitting, 기울기 손실 등의 또다른 문제가 발생할 위험이 있다.
참고로 읽어볼 만한 자료 | Dilated Convolution
