기본 레이어 이해하기 시리즈
Deconvolution
합성곱, 선형변환 등의 방법으로 차원축소된 데이터는 정보의 소실이 발생한다.
Deconvolution Layer는 이 때 손실된 정보를 복원하는 일을 한다.
Deconvolution은 여러 가지 의미로 사용되지만, 수학적으로는 정확히 Convolution 연산의 역연산을 가리키는 개념이다. 그렇다면 과연 프로그래밍적으로 완전한 역연산을 구현할 수 있을까?
결합은 분해의 역순?
합성곱 연산을 수식으로 표현하면 다음과 같다.
여기서 h(x)는 input 데이터이고, g(x)는 필터(+풀링) 연산, h(x)는 피처 맵에 해당한다. 즉, h(x)와 g(x)를 가지고 f(x)에 근사할 수 있다면 데이터를 복원하는 것과 같다고 할 수 있다.
그럼 이제 구체적인 방법을 생각해보자.
합성곱 연산 과정은 각 커널의 값을 윈도우에 곱한 후 전부 더한다. 우리는 커널의 값과 피처 맵의 최종 output 값을 알고 있지만, 원본 값과 어떤 식으로 더해졌는지는 모른다.
<A> <k> <F>
[3][4][2] [1][1] [19][14]
[5][7][1] >> [1][0] >> [15][13]
[3][0][5]convolution layer에서 위와 같은 단순한 연산을 거쳤다고 가정해보자.
출력된 피처 맵 에 대하여 값인 19를 가지고 원본 데이터 의 값을 바로 알 수 있을까? 가능한 조합의 수는 임의의 숫자 4개를 더해서 19가 되는 경우의 수와 같다. 수식으로는 다음과 같이 나타낼 수 있다.
를 만족하는 (a, b, c, d)의 조합
당장 자연수가 아닌 정수로만 범위를 확장해도 경우의 수는 무한대로 수렴한다. 쉽게 말해서 불가능하다. 따라서 정확한 수학적 역연산이 아니라 다른 방법이 필요하다.
Upsampling
데이터의 효율적 연산을 위해 차원을 축소하는 과정을 Downsampling이라고 하는데, 반대로 데이터의 크기를 역으로 늘리는(차원을 확대하는) 과정을 Upsampling 이라고 한다.
upsampling을 이용하면 피처 맵을 가지고 이미지를 생성할 수 있다. 물론 추가로 데이터를 생성하는 방법도 여러 가지가 있다. 이를 보간한다고 하는데, 크게 3가지의 보간법이 있다.
- Nearest Neighbor : 복원해야 할 값을 가까운 값으로 복제
- Bed of Nails : 복원해야 할 값을 0으로 처리
- Max Unpooling : Max Pooling 때 버린 값을 따로 기억해 두었다가 복원
각 보간법의 시각적 예시: 참고 링크
upsampling은 다양하게 활용될 수 있다. 예를 들어 저해상도의 이미지를 고해상도로 변환하거나, 전체 이미지에서 추출한 피처 맵 부분을 강조하는 효과를 낼 수도 있고, 임의의 이미지에 특정한 패턴을 입힐 수도 있다. 새로 생성한 이미지를 가지고 모델을 더 잘 훈련시킬 수도 있는데, 이게 바로 GAN의 핵심 아이디어이기도 하다.
Transpose Convolution
Transpose Convolution (이하 TC)를 활용하면 엄밀한 의미의 deconvolution까진 아니지만 비슷한 효과를 얻을 수 있다. TC 말고도 여러 가지 deconvolution 방법론이 있지만 그 자체로 하나의 분야이므로 여기서는 자주 언급되는 transpose convolution만 간단하게 살펴보자.
TC의 기본 아이디어는 합성곱 연산을 통해 얻어낸 피처 맵과 원본 이미지를 각각 input 데이터와 정답 데이터로 삼아 학습을 통해 원본 이미지에 가깝게 새로운 이미지를 생성하는 것이다.
바로 여기서 Deconvolution과 개념적 차이가 생긴다. Deconv 연산은 합성곱 연산 과정에서 사용한 커널을 그대로 재사용한다. 즉, 학습 과정이 일어나지 않는다. 반면 TC는 연산 과정에서 커널 값이 업데이트된다.
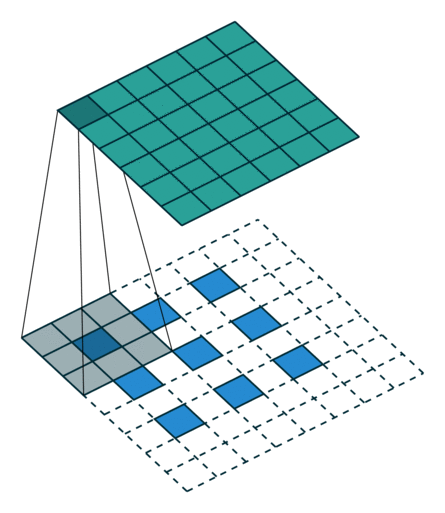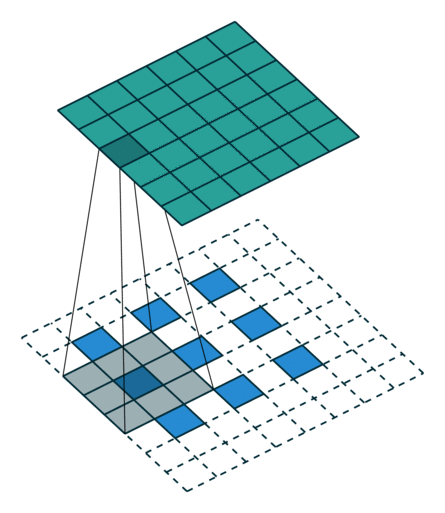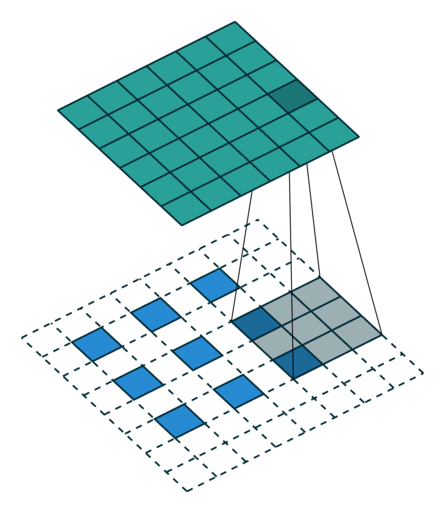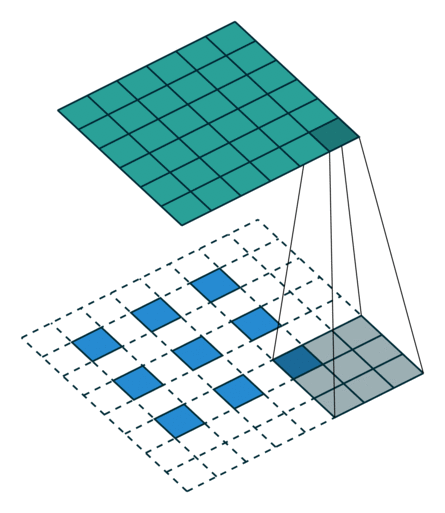
(출처: https://github.com/vdumoulin/conv_arithmetic)
위 그림을 보면 Transpose Convolution 과정을 쉽게 이해할 수 있다. 파란색이 input이고 청록색이 output 이미지이다. 합성곱 연산 과정을 역으로 따라가기 때문에 TC 연산에 사용되는 필터의 크기는 합성곱 연산에서 사용한 필터 크기와 같아야 한다.
연산 과정을 자세히 살펴보면 피처 맵의 각 원소 주변을 보간하여 input 데이터로 사용하는 것을 알 수 있다.
Auto Encoder
Auto Encoder는 이름처럼 학습한 이미지와 유사한 이미지를 생성해내는 역할을 한다. TC를 사용할 수도 있고 사용하지 않고 구현할 수도 있다.
Transpose Convolution을 사용하지 않는 Auto Encoder
먼저 TC를 사용하지 않는 오토인코더를 만들어 보자.
import numpy as np
from tensorflow.keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D
from tensorflow.keras.models import Model
from tensorflow.keras.datasets import mnist
import json
import matplotlib.pyplot as plt
# data load
(x_train, _), (x_test, _) = mnist.load_data()
x_train = np.expand_dims(x_train, axis=3)
x_test = np.expand_dims(x_test, axis=3)
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.오토인코더에는 y_test나 y_train이 없다. 원본과 가까운 이미지를 생성하는 것이 목적이기 때문이다. 따라서 자기 자신(이 경우엔 x_train)을 라벨로 삼는다.
# input
input_shape = x_train.shape[1:]
input_img = Input(shape=input_shape)
# encoder
encode_conv_layer_1 = Conv2D(16, (3, 3), activation='relu', padding='same')
encode_pool_layer_1 = MaxPooling2D((2, 2), padding='same')
encode_conv_layer_2 = Conv2D(8, (3, 3), activation='relu', padding='same')
encode_pool_layer_2 = MaxPooling2D((2, 2), padding='same')
encode_conv_layer_3 = Conv2D(4, (3, 3), activation='relu', padding='same')
encode_pool_layer_3 = MaxPooling2D((2, 2), padding='same')
encoded = encode_conv_layer_1(input_img)
encoded = encode_pool_layer_1(encoded)
encoded = encode_conv_layer_2(encoded)
encoded = encode_pool_layer_2(encoded)
encoded = encode_conv_layer_3(encoded)
encoded = encode_pool_layer_3(encoded)
# decoder
decode_conv_layer_1 = Conv2D(4, (3, 3), activation='relu', padding='same')
decode_upsample_layer_1 = UpSampling2D((2, 2))
decode_conv_layer_2 = Conv2D(8, (3, 3), activation='relu', padding='same')
decode_upsample_layer_2 = UpSampling2D((2, 2))
decode_conv_layer_3 = Conv2D(16, (3, 3), activation='relu')
decode_upsample_layer_3 = UpSampling2D((2, 2))
decode_conv_layer_4 = Conv2D(1, (3, 3), activation='sigmoid', padding='same')
decoded = decode_conv_layer_1(encoded)
decoded = decode_upsample_layer_1(decoded)
decoded = decode_conv_layer_2(decoded)
decoded = decode_upsample_layer_2(decoded)
decoded = decode_conv_layer_3(decoded)
decoded = decode_upsample_layer_3(decoded)
decoded = decode_conv_layer_4(decoded)
# compile
autoencoder = Model(input_img, decoded)
autoencoder.summary()
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')당연히 input shape와 패딩도 자기 자신과 동일하게 설정한다.
인코더는 디코더의 출력을 입력으로 받는다.
디코더 마지막 레이어의 활성화 함수는 Sigmoid를 사용하므로, loss 함수도 binary_crossentropy를 사용한다.
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 28, 28, 1)] 0
conv2d (Conv2D) (None, 28, 28, 16) 160
max_pooling2d (MaxPooling2D (None, 14, 14, 16) 0
)
conv2d_1 (Conv2D) (None, 14, 14, 8) 1160
max_pooling2d_1 (MaxPooling (None, 7, 7, 8) 0
2D)
conv2d_2 (Conv2D) (None, 7, 7, 4) 292
max_pooling2d_2 (MaxPooling (None, 4, 4, 4) 0
2D)
conv2d_3 (Conv2D) (None, 4, 4, 4) 148
up_sampling2d (UpSampling2D (None, 8, 8, 4) 0
)
conv2d_4 (Conv2D) (None, 8, 8, 8) 296
up_sampling2d_1 (UpSampling (None, 16, 16, 8) 0
2D)
conv2d_5 (Conv2D) (None, 14, 14, 16) 1168
up_sampling2d_2 (UpSampling (None, 28, 28, 16) 0
2D)
conv2d_6 (Conv2D) (None, 28, 28, 1) 145네트워크 구조를 보면 실질적인 shape의 변화는 MaxPooling2D와 UpSampling2D에서만 일어난다는 것을 알 수 있다.
shape의 변화를 자세히 살펴보자. 원본 이미지 크기는 (28, 28, 1)인데 첫 MaxPooling 레이어의 파라미터가 (2, 2)이고, Convolution Layer에서 지정한 필터 개수가 16개이기 때문에 (28, 28, 1)에서 (14, 14, 16)으로 변환된다. 이어서 두 번째 MaxPooling 레이어를 거치며 (7, 7, 8)로 바뀌고, 최종적으로는 (4, 4, 4) 형태로 인코더에서 출력된다.
디코더는 (4, 4, 4) 모양의 데이터를 입력받아 UpSampling 레이어를 거쳐 다시 (8, 8, 4) 모양으로 바꾼다. UpSampling 레이어를 계속 거쳐 최종적으로는 원본 이미지의 모양과 동일한 (28, 28, 1)로 변환된다.
얼마나 원본과 같을까?
그런데 모양이 같다고 데이터가 동일한 건 아니다.
UpSampling 레이어의 디폴트 옵션은 nearest이다. 가까운 데이터를 그대로 가져온다는 뜻이므로, 실제 데이터와는 당연히 차이가 생길 수 밖에 없다.


위쪽은 원본 이미지이고 아래쪽은 오토인코더를 사용하여 생성한 이미지이다. nearest 옵션을 주었으니 당연히 경계가 잘 구분되지 않을 수밖에 없다.
그렇다고 네트워크 구조가 잘못된 것은 아니다. 애초에 epoch 수도 10밖에 되지 않거니와 Variational Autoencoder나 DCGAN 같은 모델은 동일한 디코더 구조를 가지고 훨씬 좋은 성능을 뽑아내기 때문이다.
그렇다면 Transpose Convolution을 사용하면 얼마나 좋은 성능이 나오는지 실험해보자.
Transpose Convolution을 사용하는 Auto Encoder
기본적인 네트워크 구조는 동일하되, Conv2D 레이어를 Conv2DTranspose 레이어로 바꿔주면 된다.
from tensorflow.keras.layers import Conv2DTranspose
# Conv2DTranspose
# input
input_shape = x_train.shape[1:]
input_img = Input(shape=input_shape)
# encoder
encode_conv_layer_1 = Conv2D(16, (3, 3), activation='relu')
encode_pool_layer_1 = MaxPooling2D((2, 2))
encode_conv_layer_2 = Conv2D(8, (3, 3), activation='relu')
encode_pool_layer_2 = MaxPooling2D((2, 2))
encode_conv_layer_3 = Conv2D(4, (3, 3), activation='relu')
encoded = encode_conv_layer_1(input_img)
encoded = encode_pool_layer_1(encoded)
encoded = encode_conv_layer_2(encoded)
encoded = encode_pool_layer_2(encoded)
encoded = encode_conv_layer_3(encoded)
# decoder
decode_conv_layer_1 = Conv2DTranspose(4, (3, 3), activation='relu', padding='same')
decode_upsample_layer_1 = UpSampling2D((2, 2))
decode_conv_layer_2 = Conv2DTranspose(8, (3, 3), activation='relu', padding='same')
decode_upsample_layer_2 = UpSampling2D((2, 2))
decode_conv_layer_3 = Conv2DTranspose(16, (3, 3), activation='relu')
decode_upsample_layer_3 = UpSampling2D((2, 2))
decode_conv_layer_4 = Conv2DTranspose(1, (3, 3), activation='sigmoid', padding='same')
decoded = decode_conv_layer_1(encoded) # Decoder는 Encoder의 출력을 입력으로 받습니다.
decoded = decode_upsample_layer_1(decoded)
decoded = decode_conv_layer_2(decoded)
decoded = decode_upsample_layer_2(decoded)
decoded = decode_conv_layer_3(decoded)
decoded = decode_upsample_layer_3(decoded)
decoded = decode_conv_layer_4(decoded)
# compile
autoencoder = Model(input_img, decoded)
autoencoder.summary()
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')결과는 다음과 같다.


생각보다 큰 차이가 없다. 위에서 언급했다시피 nearest 옵션을 변형하지 않는 이상 생성하는 이미지의 경계 구분은 어려울 것이다. 그렇다면 어떤 방법을 써야 효율적이고 성능이 좋은 Deconvolution 모델을 만들 수 있을까?
이런 고민을 통해 오토인코더의 디코더 개선 과정에서 영감을 얻어 만들어진 것이 바로 GAN이다.
참고할 만한 링크 | Transpose와 Upsampling
