- 전체보기(7)
- 선형대수(4)
- 통계수학(3)
- Object Detection(1)
- confusion matrix(1)
- Producting Serving(1)
- 평가지표(1)
- 회귀분석(1)
- iou(1)
- 논문 리뷰(1)
- airflow(1)
- Map(1)
- meta learning(1)
MAML 소개
Abtract 이 논문은 모델에 관계 없이 적용 가능한(model-agnostic) meta-learning 알고리즘을 제안한다. 이 알고리즘은 Gradient descent로 훈련된 모든 모델과 호환되며 분류, 회귀, 강화 학습 등 다양한 학습 문제에 적용될 수 있다

행렬의 계수, rank
1. 열공간(column space)과 행공간(row space) $m\times n$ 행렬 $A$ n개의 열벡터에 의해 생성되는 $\mathbb{R}^m$의 부분 공간을 A의 열공간(column space)이라고 한다. m개의 행벡터에 의해 생성되는 $\mathbb
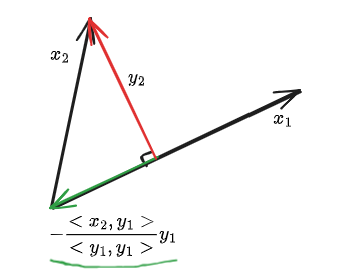
벡터 공간의 기저와 차원, 정규 직교 기저, 그람-슈미트 정규직교화
벡터 공간 S에 있는 벡터의 집합 ${x_1,x_2,\\dots,x_n}$에 대하여 다음을 만족하면 ${x_1,x_2,\\dots,x_n}$은 S의 기저(basis)이다. 1\. ${x_1,x_2,\\dots,x_n}$ spans the vector space S.2\
벡터 공간, 선형 결합, 생성 집합, 내적, 선형 독립, 선형 종속
벡터들을 포함하는 집합 S가 다음을 만족할 때 이를 벡터 공간(vector space)라고 한다. (ⅰ) O ∈ S (ⅱ) x ∈ S, y ∈ S 이면 x+y ∈ S. (closed for addition) (ⅲ) x ∈ S 이면, 임의의 실수 α에
행렬 및 벡터 표기법
앨빈 C. 렌쳐의 책 'Linear models in statistics'을 읽고 정리한 내용입니다. 2.1 행렬 및 벡터 표기법 2.1.1 Matrices, Vectors, and Scalars matrix, 행렬 행렬을 나타내기 위해 대문자 굵은 글씨를 사용하

Window에서의 Airflow실습: Airflow 설치
내가 가지고 있는 노트북이 Window 환경이기 때문에 Vscode 내의 wsl Terminal에서 진행하였다. ctrl+단축키로 터미널창을 열어주고, +버튼 옆 꺽쇠를 눌러 WSL을 연다. !\[](https://velog.velcdn.com/images/o
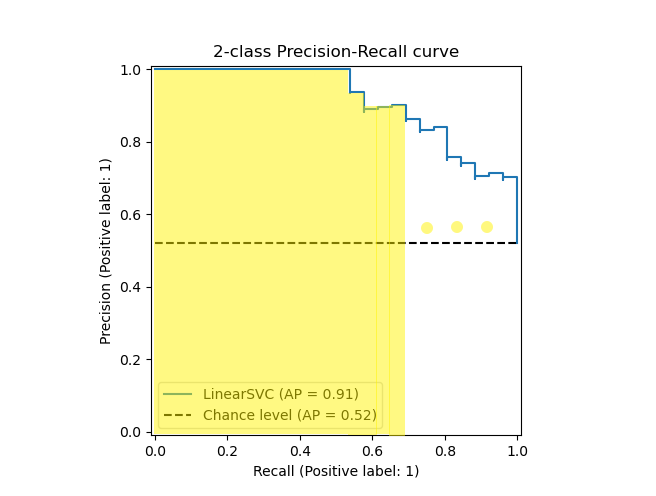
Evaluation of Object Detection
이 포스트에서는 Object Detection에서 많이 사용되는 평가지표에 대해 알아보겠습니다. 모델이 객체를 얼마나 잘 잡아내느냐 평가하는 성능 평가, 모델이 얼마나 빠르게 돌아가느냐 평가하는 속도 평가로 나누어 살펴보겠습니다. 1. 성능 평가 얼마나 잘 객체를 탐지
