[Paper Review] - Unlocking the Power of Patch: Patch-Based MLP for Long-Term Time Series Forecasting(AAAI, 2025)
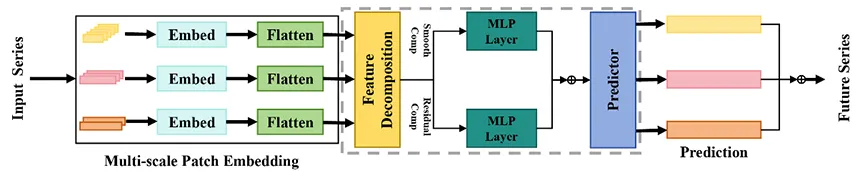
장기 시계열 예측 문제에서 MLP에 Patching을 적용한 PatchMLP라는 새로운 모델을 제안Transformer가 장기 시계열 예측(Long-Term Time Series Forecasting, LTSF) 과제의 해법이 될 수 있는지 회의적.패치 메커니즘을 적용
[Paper Review] - Not All Data are Good Labels: Onthe Self-supervised Labeling for Time Series Forecasting(2025.02)
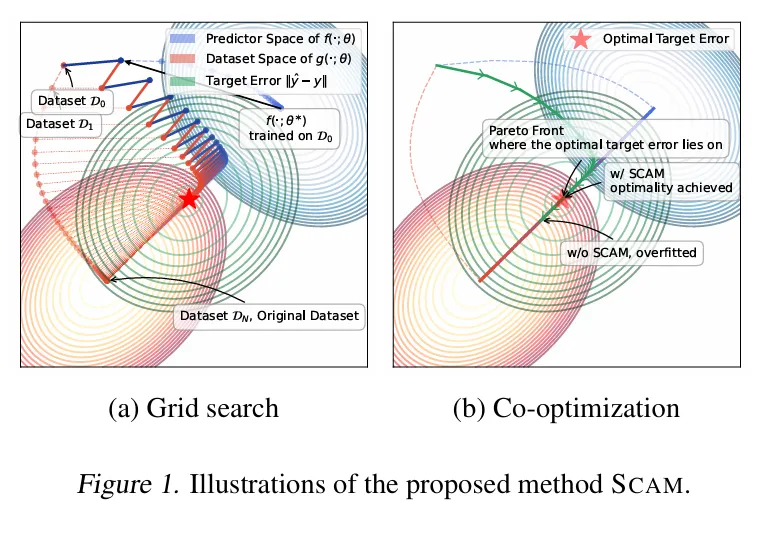
Self-supervised leaerning을 활용한 라벨 보정 :기존의 원시 라벨(raw labels)이 가진 노이즈와 과적합 문제를 완화하기 위해, 재구성(reconstruction) 네트워크를 이용하여 후보 데이터셋(candidate datasets)을 생성하고
[Paper Review] - W-MSE(Whitening Mean Squared Error, 2021, ICML)
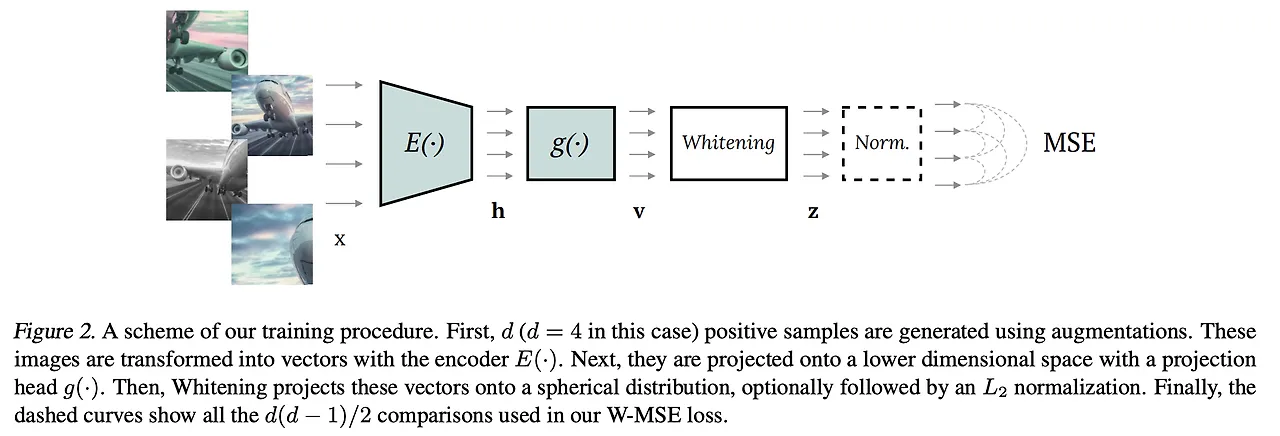
Whitening MSE(W-MSE)라는 새로운 Self supervised learning loss function을 제안.배치 샘플을 구형 분포(spherical distribution)에 놓이도록 제약하며, 기존 positive-negative instance c

[Paper Review] - Soft Contrastive Learning for Time Series (SoftCLT), ICLR 2024
시계열 데이터에 특화된 Soft Contrasive Learning 전략을 제안다양한 다운스트림 작업에서 기존 contrasive learning 방법론 모델들보다 좋은 성능을 보임plug - and - play 방식이기 때문에 다른 모델 프레임워크에 쉽게 적용시킬 수
Batch Normalization(배치 정규화)
Batch Normalization은 학습 과정에서 각 배치 단위 별 다양한 분포를 가진 데이터를 각 배치별로 평균과 분산을 이용해 정규화하는 것이다.Batch Normalization는 별도의 과정으로 있는 것이 아닌, 신경망 안에 포함되어 학습시 평균과 분산으로 조
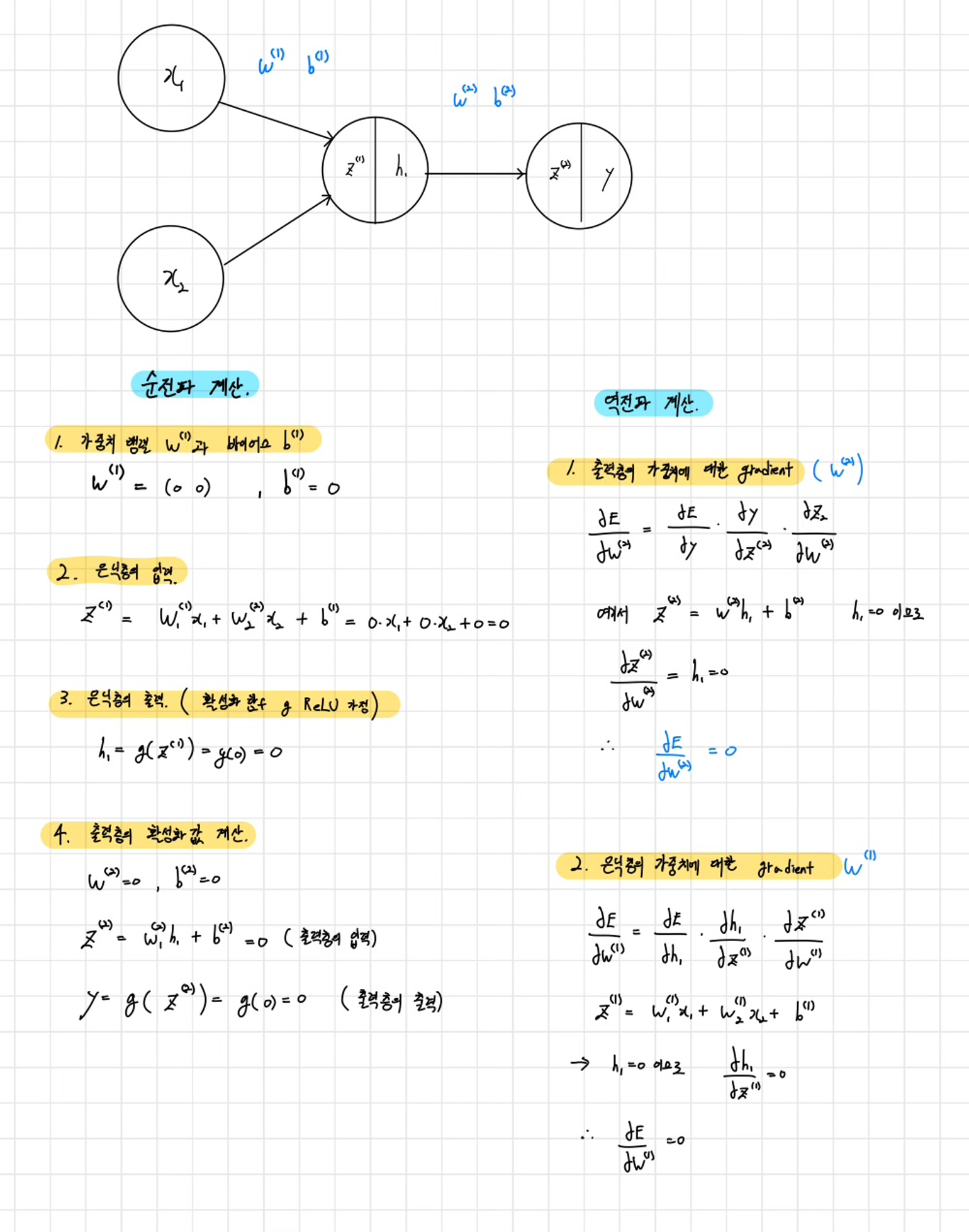
가중치 초기화(Weight initialization)
가중치 초기화란?(Zero Initialization (제로 초기화)( - 가중치의 초깃값을 모두 0으로 설정하면 어떻게 될까?( - 이유(Xavier Initialization (자비에 초기화)( - 기본 아이디어( - 수식( - 정규분포 (Ga
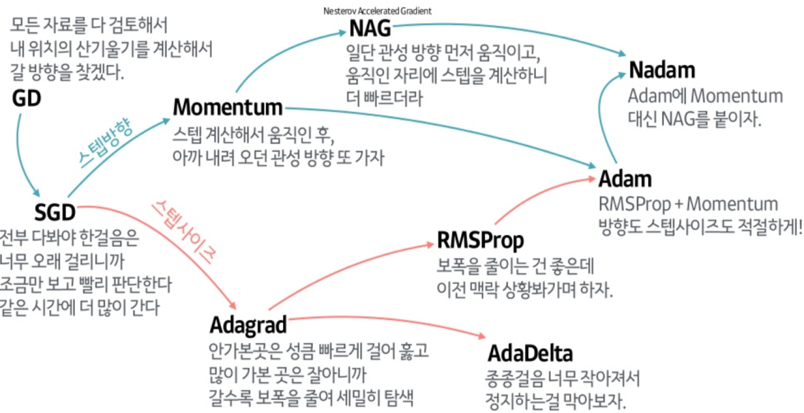
최적화 알고리즘 - RMSProp,Adam
RMSProp(Root Mean Square Propagation)은 Adagrad의 단점을 보완하기 위해 등장했다. Adagrad는 학습률이 점점 작아져 학습이 멈추는 문제가 있는데, RMSProp은 이를 해결하려고 고안된 알고리즘이다.RMSProp의 핵심 아이디어는
최적화 알고리즘 - SGD, Momentum, Nesterov momentum, Adagrad
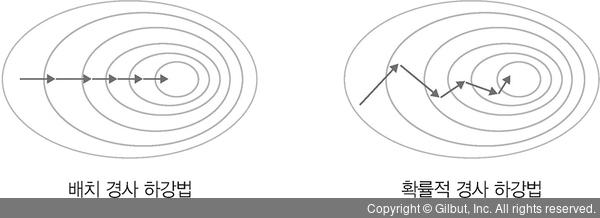
최적화 알고리즘 - SGD, Momentum, Nesterov momentum, Adagrad 참고자료 >밑바닥부터 시작하는 딥러닝 >https://velog.io/@cha-suyeon/DL-최적화-알고리즘 들어가기에 앞서 신경망 학습의 목적은 손실 함수의 값
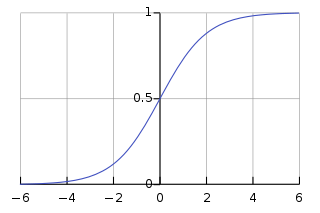
기울기 소실 문제(Problem Vanishing Gradient)
참고자료 https://ydseo.tistory.com/41gradient 기반의 method는 parameter value의 작은변화가 network output에 얼마나 영향을 미칠지를 이해하는 것을 기반으로 parameter value를 학습시킨다.만약
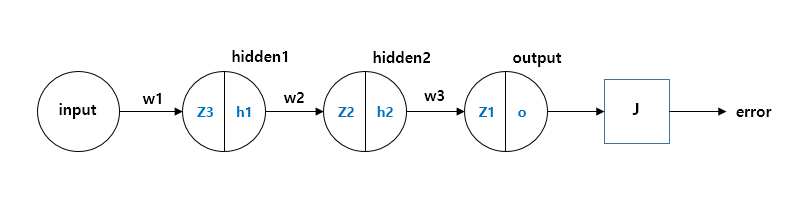
손으로 공부하는 역전파(BackPropagation)
예시z1,z2,z3: 각 레이어의 노드 출력과 가중치의 합성곱.h1,h2,h3h_1, h_2, h_3h1,h2,h3: 각각 z1,z2,z3 값의 활성화 함수, 즉 시그모이드 함수의 결과 (각 노드의 출력). z1,z2,z3z_1, z_2, z_3 J: 시스템의 에러
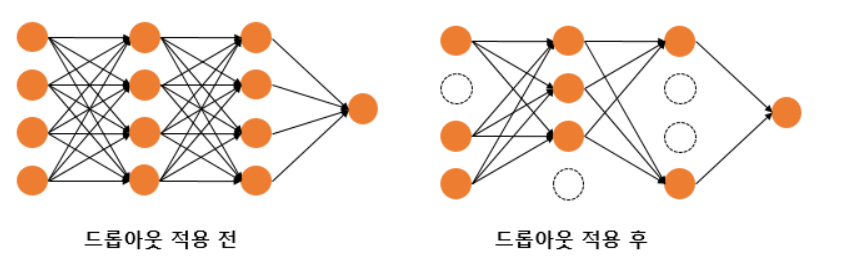
과적합 방지 기법(딥러닝)
데이터 수가 적은 경우모델의 파라미터가 많은 경우딥러닝 모델은 고전 머신러닝 모델에 비해 압도적으로 파라미터가 많기 때문에 과적합이 되기 쉬움데이터 양 증가: 충분한 데이터가 있으면 모델이 일반적인 패턴을 학습하여 과적합을 방지할 수 있습니다. 데이터가 부족한 경우에는
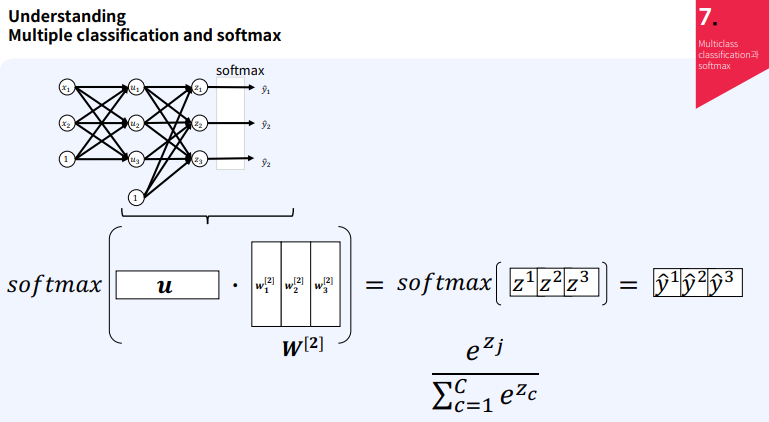
다중 클래스 분류와 소프트맥스 함수
다중 클래스 분류는 여러 개의 클래스 중 하나를 예측하는 문제이다. 이를 위해 신경망을 사용하여 각 클래스에 대한 확률을 계산하고, 가장 높은 확률을 가진 클래스를 선택하게 된다. 입력층 (Input Layer):입력 데이터 ( x_1 ), ( x_2 )를 포함보통 b
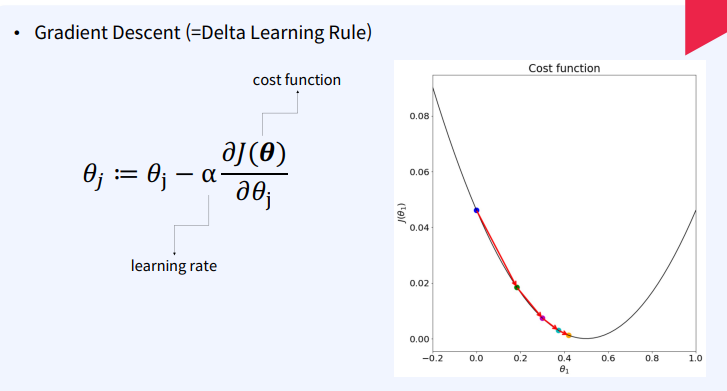
Gradient descent
✔ Gradient Descent란?Gradient Descent는 함수의 매개변수 값을 반복적으로 조정하여 주어진 함수를 최소화하는 최적화 알고리즘입니다. 이 알고리즘의 목적은 함수의 최소값을 제공하는 매개변수 값을 찾는 것입니다. 머신 러닝에서는 주로 비용 함수나
Loss function, cost function 차이점
정의: 개별 훈련 예측의 오차를 측정합니다.용도: 각 데이터 포인트에 대해 모델의 예측이 실제 값과 얼마나 다른지를 계산합니다.예시: MSE (Mean Squared Error), MAE (Mean Absolute Error), Cross-Entropy Loss 등.정

