Paper: Interpretable Convolutional Neural Networks
Code : github.com

0. Abstract

본 논문은 CNN 내 high conv-layer에서 지식 표현을 더 명확하게 하기 위해 전통적인 CNN을 Interpretable CNN으로 수정하는 방법을 제안한다. 해석가능한 CNN에서는 high conv-layer 내 각 필터가 구체적인 object의 part를 표현한다. 특히, object part나 texture의 annotation을 추가하지 않아도 전통적인 CNN의 학습 방법과 같은 방식을 활용해학습할 수 있다. 해석가능한 CNN은 학습 과정에서 자동적으로 high conv-layer내 각 filter를 각 object part에 할당한다. 이 방법은 CNN기반으로 하는 다양한 구조에 적용될 수 있다. 해석가능한 CNN가 생성하는 명시적인 지식 표현(explicit knowledge representation)은 사람으로 하여금 CNN 내 logic을 이해할 수 있게 해준다. 예를 들어, CNN이 예측할 때 어떤 패턴을 기억하는지 등.. 그 외에도 전통적인 CNN보다 해석가능한 CNN 내 필터가 더 의미 깊은 해석을 보여준다는 결과 또한 존재한다.

1. Introduction

CNN은 object classification, detection 등의 task에서 괄목할 만한 성능을 보여왔지만, 해석력은 항상 CNN의 아킬레스건이였다.
본 논문에서는, 다음과 같은 문제에 초점을 둔다.

• 추가적인 human supervision(지도) 없이, CNN을 conv-layer로 하여금 해석가능한 지식 표현을 획득할 수 있게끔 수정할 수 있을까?

우리는 CNN이 end-to-end 학습 과정 중에 representation에 대한 특정한 introspetion(자기 성찰)을 얻기를 기대하고, 이로부터 높은 해석가능성을 보장하기 위해 representation을 regularize?(정규화) 할 수 있기를 원한다. CNN의 해석가능성을 높히는 문제는 전통적인 off-line visualization과 pre-trained CNN representation의 diagnosis(LIME, SHAP, Grad-CAM 등 post-hoc XAI method)과는 다른 문제이다(본 논문 내 예시 레퍼런스 존재).

Bau et al[paper]은 CNN 내 존재하는 6가지의 semantics(의미, 의미론)를 정의했는데, 이는 objects, parts, scenes, textures, materials, colors로 이루어진다. 사실상, objects와 parts는 특정한 shape를 갖는 object-part patterns으로 여길 수 있고, 나머지 4개는 명확한 contour가 없는 texture pattern으로 여길 수 있다. 또한, low conv-layer의 filter는 보통 간단한 texture를 묘사하는 반면에, high conv-layer는 보통 objet parts를 묘사하곤 한다.

따라서, 본 연구에서는 high conv-layer의 filter가 object part를 학습하는 데 초점을 맞춘다. 아래 그림은 전통적인 CNN과 우리의 interpretable CNN 사이의 차이점을 나타낸다.

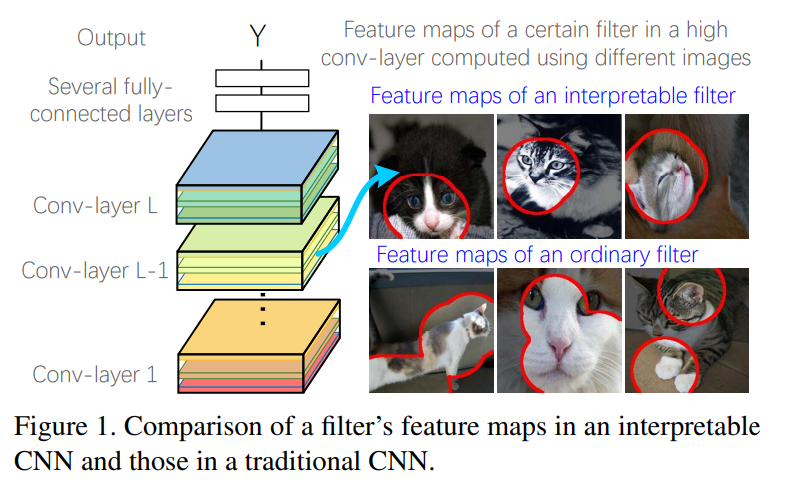
이 때 original CNN의 high-layer filter들은 mixture of patterns을 묘사한다(예를 들어, 고양이의 다리와 머리 두 가지에 의해 필터가 활성화될 수 있다). 이처럼 복잡한 representation은 network의 설명력을 약화시킬 수 있다.
대조적으로, 우리의 interpretable CNN의 필터들은 특정 부위에 의해서만 활성화된다. 이런 방식으로, 분류를 위한 CNN의 필터에 의해 어떤 object part를 인지하는 지 명시적으로 설명할 수 있게 된다. 요약하면, 연구의 목표는 아래와 같다.

• CNN의 설명력을 개선하되, 다양한 구조를 가진 CNN에 적용될 수 있게끔 CNN을 약간만 수정한다.
• 지도를 위한 object parts나 texture의 annotation은 필요 없어야 한다(부분적인 비지도학습). 대신, 각 filter가 object part를 자동적으로 학습할 수 있게끔 한다.
• 해석가능한 CNN은 top layer의 loss function을 바꿔선 안되며, original CNN과 같은 학습 방법을 사용한다.
• 연구 조사 결과, 해석 가능성을 목표로 하는 구조 설계는 분류 성능을 약간 낮출 수 있다. 하지만, 우리는 최대한 성능 저하를 제한하는 쪽으로 연구를 진행하였다.

Method
우리는 CNN의 특정 conv-layer에 있는 filter가 object part의 표현을 학습하기 위해, 간단하지만 효율적인 loss를 제안한다. 즉, 각 filter의 output feature map에 대한 loss를 도입한다.

위의 그림에 간략히 나타난 loss는, 카테고리 간 activation에 대해 낮은 entropy와 neural activation의 공간 분포에 대해 낮은 entropy를 격려한다. 예를 들면,

1. 각 filter는 하나의 category에 의해 배타적으로(exclusively) 포함된 distinct (?)object part를 encode해야한다.
   • 각 filter가 object의 일부분(예를 들어, 고양이의 얼굴, 사람의 팔 등(불확실))만을 학습해야 한다는 말이다.
2. 다양한 object region에 반복적으로 나타나는 게 아니라, object의 single part에 의해서 filter가 활성화되어야 한다.
   • 아마 object 내 하나의 part는 하나의 filter에만 영향을 끼쳐야 한다는 말이다.

우리는 다양한 region들에 존재하는 반복적인 shape가 low-level texture(색, 모서리 등)를 묘사할 가능성이 high-level parts을 묘사할 가능성보다 높다고 가정한다. 예를 들면, 왼쪽 눈과 오른쪽 눈은 다른 filter에 의해 represented 될 수 잇는데, 두 눈이 대칭적이긴 하지만, 같지는 않기 때문이다.

The value of network interpretability
high conv-layer의 명확한 semantics는 우리가 사람으로 하여금 네트워크의 판단을 신뢰하게끔 할 때 아주 유용하다. dataset이나 reprensetations의 편향을 고려할 때, test image의 높은 accuracy로는 CNN이 올바른 representation을 encode할 지 보장하긴 힘들다.

• 예를 들면, face image에서 CNN은 'lipstick'을 인지하는 데 eye feature라는 잘못된 context를 사용할 수도 있다.

따라서, CNN이 의미적으로, 그리고 시각적으로 CNN 내부의 논리를 설명하지 않는 이상, 인간은 network를 완전히 믿을 수 없다.

network diagnosis를 위한 최근 연구들([Interpretable Explanation..], [Grad-CAM], [LIME])은 pixel level에서 output을 예측하는 데 가장 많이 기여한 image region을 localize한다.
하지만 본 연구에서는, object-part level에서 CNN이 작동 원리를 설명하길 기대한다. 해석가능한 CNN이 주어졌을 때, 우리는 object classification을 위한 CNN에 의해 기억되는 object part의 분포를 명시적으로 보여줄 수 있게 된다.

Contributions
본 연구는 CNN 내 high conv-layer의 표현이 해석가능하게끔 CNN을 end-to-end로 학습하는 새로운 태스크에 집중했다. 이 목적을 위해 간단하지만 효과적인 CNN 수정법을 제안했으며, CNN을 포함하는 다양한 구조에 적용가능할 뿐더러 추가적인 annotation 없이 학습시킬 수 있다. Experiments는 우리의 방법이 CNN의 object-part interpretability를 향상시켰다는 것을 보여준다.

2. Related work

Network visualization
Pattern retrieval
Model diagnosis
Learning a better representation

3. Algorithm*

CNN의 target conv-layer가 주어졌을 때, 우리는 이 conv-layer 내 각 filter가 특정 category의 특정 object part에 의해서 활성화 되기를 기대한다(당연히 다른 categories의 이미지에 대해서는 활성화되지 않아야 한다). 우선, $I$를 학습 이미지의 집합이라 해보자. 이 때, $I_C\sub I$는 category $c(c=1,2,3...,C)$에 속하는 부분집합을 말한다. 이론적으로, CNN을 학습하는 데 있어서, multi-class classification, single-class classification(c=1이 특정 카테고리, c=2가 랜덤 이미지), 그리고 다른 task들에 대해서 다른 종류의 loss를 사용할 수 있다.

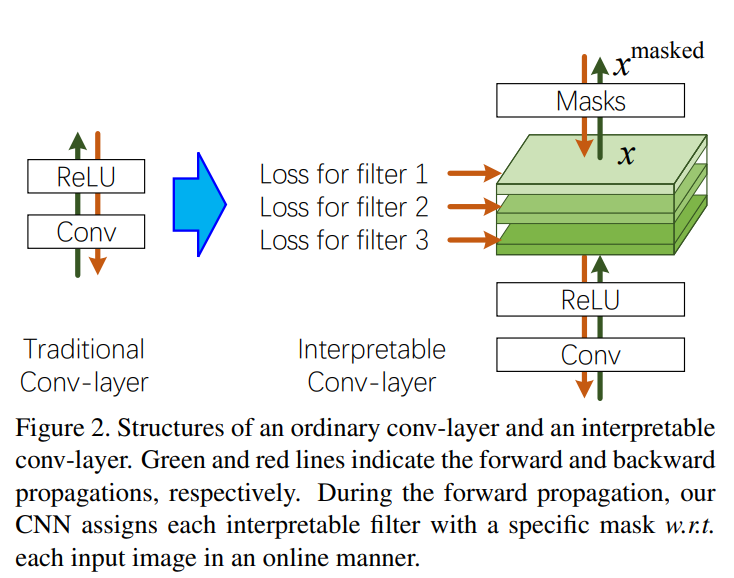
(위의)Figure 2는 우리의 interpretable conv-layer을 보여준다. 다음 단락에서는, target conv-layer에 있는 단일 filter $f$의 학습에 대해서 집중적으로 다룰 것이다. 간단히 말하면, ReLu 연산 뒤에 filter $f$의 feature map $x$에 대한 loss를 추가할 것이다.

During the forward propagation, input image $I$가 주어졌을 때, CNN은 ReLU 연산 후에 filter $f$의 feature map $x$를 연산한다($x$는 $n\times n$ matrix이고, $x_{ij}\geq0$이다).
우리 방법은 feature map $x$에 있는 object part의 potential position을 매우 강한 활성화($\hat{\mu}=argmax_{\mu =[i,j]} x_{ij}, 1\leq i, j\leq n$)를 보이는 neural unit으로 추정한다.
그 후, 추정된 part position $\hat{\mu}$을 기반으로, CNN은 noisy activation을 걸러내기 위해 feature map $x$에 특정한 mask를 할당한다.

다른 이미지가 주어졌을 때, $f$에 대응하는 object part가 $n^2$의 다양한 위치에 나타날 수 있기 때문에, 우리는 filter $f$를 위한 $n^2$ template을 정의한다($\{ T_{\mu_1},T_{\mu_2}, T_{\mu_3}, ..., T_{\mu_{n^2}}\}$). 아래의 Figure 3에 보이는 것처럼, 각 템플릿 $T_{\mu_i}$는 $n\times n$의 행렬이며, 이는 target part가 주로 feature map $x$에 있는 $i$번째 unit을 촉발할 때, feature map $x$에 대한 이상적인 활성화 분포를 묘사한다(?).

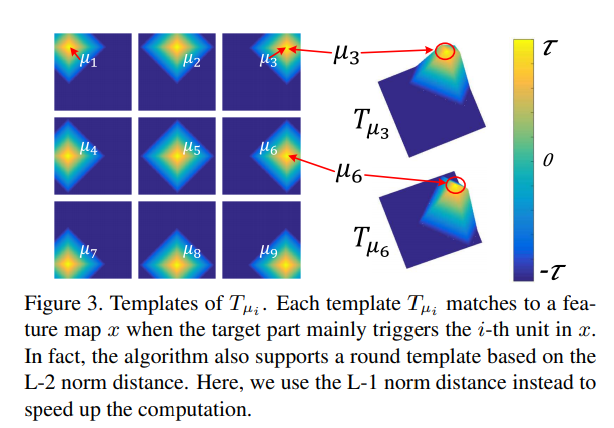
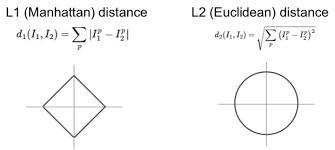
우리의 방법은 $n^2$ 템플릿에서 나온 part position $\hat{\mu}$에 대한 템플릿 $T_{\hat{\mu}}$을 mask로 선택한다. 그리고, output masked feature map으로서 $x^{masked}=max\{x\circ T_{\hat{\mu}}, 0 \}$를 연산한다($\circ$ 는 Hadamard product).

※ L1 norm, L2 norm?

그 다음, 아래의 Figure 4는 다양한 이미지들에 대해 선택된 masks $T_{\hat{\mu}}$ 를 시각화하고, original과 masked feature map을 비교하는 모습을 보여준다.

CNN은 다른 이미지에 대해 각기 다른 템플릿을 선택한다. Mask operation은 Gradient Back-Propagation을 support(?)한다.

위의 템플릿 관련한 개념은 $\tau$가 어떻게 정해지는 지를 중점으로 이해하면 될 듯 하다.

During the back-propagation process, 우리의 loss는 filter $f$가 category $c$의 특정한 object part를 표현하게끔 하고, 다른 category의 이미지에 대해서는 반응하지 않게끔 한다.
(본 글 내 Section 3.2에서 filter $f$에 대한 category $c$의 결정 방법이 있음)
아무튼, $X$를 $X=\{x|x=f(I), I\in \bold{I}\}$라 정의하고, 이를 다양한 트레이닝 이미지에 대한 'ReLU 연산 이후 filter $f$의 feature map'이라 정의하자. input image $I$가 주어졌을 때, 만약 $I\in I_c$라면 우리는 feature map $x=f(I)$가 할당된 템플릿 $T_{\hat{\mu}}$에 fitting 되는 것을 기대한다. 반면, $I\notin I_c$라면, negative 템플릿인 $T^{-}$를 고안하고, feature map $x$가 $T^{-}$에 매칭되길 바란다.
단, forward propagation 동안은, negative 템플릿을 사용하지 않고 다른 categories를 포함한 모든 feature maps은 마스크로 $n^2$ 템플릿을 선택한다.

따라서, 각 feature map $x$는 $n^2+1$개의 템플릿 중 하나에 배타적으로 fitting 되어야 한다(negative 템플릿 1개와 기존의 템플릿 $n^2$개). 그 후, 우리는 filter $f$의 loss에 대한 연산을 '$X$와 $T$ 사이의 minus mutual information'으로서 연산한다.
($X$는 feature map이고, $T$는 템플릿)

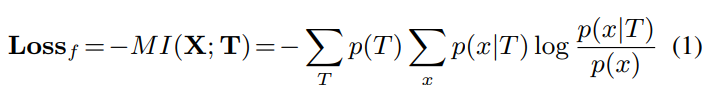
템플릿에 대한 사전 분포는 $p(T_{\mu})= {{\alpha}\over {n^2}}$, $p(T^{-})=1-\alpha$로 주어진다($\alpha$: (상수) 사전 우도).

템플릿은 $n^2$의 경우의 수가 있으며, 이를 모두 고려하면 positive template은 $\alpha$의 확률을, negative template은 $1-\alpha$의 확률을 보이는 것을 알 수 있다.

feature map $x$와 템플릿 $T$ 사이의 fitness는 조건부 우도인 $p(x|T)$로 추정한다.

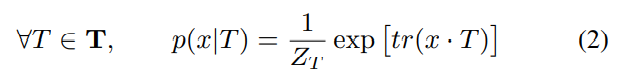
이 때, $Z_T=\sum_{x\in X} exp[tr(x*T)]$이다. $x*T$는 $x$와 $T$의 곱이고, $tr(*)$는 행렬의 trace를 뜻한다. 즉, $tr(x*T)=\sum_{ij}x_{ij}t_{ij}$이다.

trace는 그저 feature map과 template이 Element-wise product한 것을 간단히 나타낸 것 뿐이다. 즉, 직관적으로 보자면, 'feature map $x$와 template $T$가 (다른 feature map들에 비해) 얼마나 유사한가?' 정도로 볼 수 있다.

당연히 위 식의 $exp$는 softmax 형태를 만들어주기 위함이다. 자세히는, logit, sigmoid 등에서 softmax까지 이어지는 개념들 참고.

$p(x)$는 $p(x)=\sum_Tp(T)p(x|T)$로 정의된다.

위 식은 단순히 (분할된) 이산확률분포라면 성립하는 식이다. 이쯤에서 위의 식 (1), (2)를 다시 보고 이해하는 것이 좋다.

Part templates: 위의 그림 Figure 3에서 나타난 것처럼, negative 템플릿은 $T^{-}=(t_{ij}^{-}), t_{ij}^{-}=-\tau<0$로 주어지며, 이 때 $\tau$는 양수의 상수이다. $\mu$에 대응하는 positive 템플릿은 $T_{\mu}=(t_{ij}^{+}), t_{ij}^{+}=\tau *max(1-\beta {{{||[i,j]-\mu||}_1}\over{n}}, -1)$로 주어진다. 이 때, $||*||_1$은 $L_1$ norm distance를 말하며, $\beta$또한 상수의 매개변수이다.

참고로, 위의 식들 중 일부는 본 논문의 4장(Understanding of the loss)를 곁들여야 이해할 수 있다. 그를 위해 본 블로그 글에서는 본 논문의 4장을 3.1절로, 본 논문의 3.1절(Learning)을 3.2절로 표기한다.

3.1. Understanding of the the loss*

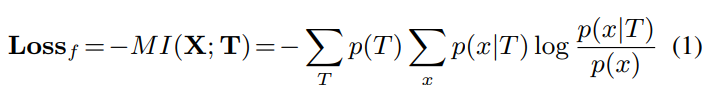
$\bold{T}^{'}=\{T^{-},\bold{T}^{+}\}$라 정의하고, $H(\bold{T})$를 $H(\bold{T})=-\sum_{T\in \bold{T}}p(T)logp(T)$, 즉 part template의 사전 엔트로피라 하자.
그러면, 위 식은 아래와 같은 식으로 다시 쓰일 수 있다.

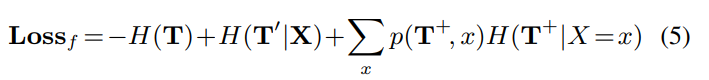
Low inter-category entropy:
우선, 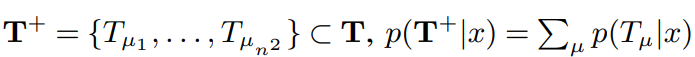라 가정하자.

이 때, 식 (5)의 두 번째 텀인 $H(\bold{T}^{'}|\bold{X})$는 아래와 같이 계산할 수 있다.

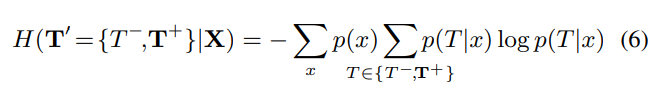
우리는 모든 positive 템플릿 집합인 $\bold{T}^{+}$를 category $c$를 표현하는 single label이라 정의한다. negative 템플릿은 category $c$ 이외의 다른 categories를 나타내기 위한 관점에서 $T^{-}$를 사용한다. 이 용어들은 inter-category activations의 낮은 조건부 엔트로피를 격려한다.

category $c$와 $others$의 엔트로피가 낮다면, 서로 구분이 잘 되도록 activation 되었다 볼 수 있다.
또한, 모든 feature map을 순회해야 하므로, 사전확률 $p(x)$가 곱해질 수 밖에 없다.

예를 들면, 잘 학습된 filter $f$는 특정 카테고리 $c$에 의해서만 배타적으로 활성화 되어야 하며, 다른 카테고리들에는 활성화되면 안 된다. 우리는 filter $f$의 feature map $x$를 'input image가 category $c$에 속하는지, 아닌지'를 판단하기 위해 사용할 수 있다.
예를 들면, 낮은 불확실성(엔트로피)라면, feature map $x$는 $T_{\hat{\mu}}$에 fitting되거나, $T^{-}$에 fitting되는지.

Low spatial entropy:

$\tilde{p}(T_{\mu}|x)={{p(T_{\mu}|x)}\over{p(\bold{T}^{+}|x)}}$이라 할 때,
방정식(5)의 세번째 식(의 일부)을 다시 쓰면 아래와 같다.

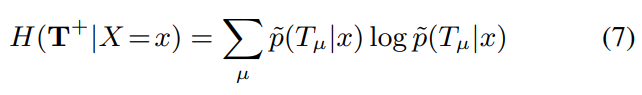
직관적으로 엔트로피 식을 이해하기 위해 $p(\bold{T}^{+}|x)=\sum_{\mu}p(T_{\mu}|x)$ 임을 참고하자.

이 term은 feature map $x$ 내 activations의 spatial distribution의 낮은 조건부 엔트로피를 격려한다. 예를 들면, image $I\in\bold{I}_c$가 주어졌을 때, 잘 학습된 filter는 오직 feature map $x$의 'single region' $\hat{\mu}$ 에 의해서만 활성화 되어야 한다. 즉, 'different location'에서 반복적으로 활성화되어선 안 된다.

3.2 Learning

학습 과정에 대해 더 정확히 살펴보자.
forward-propagation: CNN 내 각 filter가 bottom-up 방식으로 정보를 통과시킨다.

• 이는 전통적인 CNN과 거의 동일하다.

back-propagation: 해석가능한 conv-layer 내 각 filter가 filter의 feature map $x$에 대한 gradients를 $k$번째 샘플의 final task loss인 $\bold{L}(\hat{y}_k, y_k*)$와, filter loss인 $Loss_f$ 로부터 받는다. $\lambda$는 가중치이다.

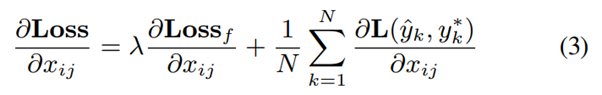
여기서 final task loss는 classification loss를 뜻할 것.
본 논문에서는 $\lambda$를 $\lambda \propto {{1}\over{t}}mean_{x\in X}max_{i,j}x_{ij}$ 로 사용함.

그 후, 위 식 (3)에서 계산한 그래디언트를 lower layer로 보내고, lower layer에 있는 parameters에 관한 Xgradient(본문 오타?)와 feature maps에 관한 gradients를 계산해, CNN을 업데이트 한다.
그 단계에서, feature map $x$의 각 요소 $x_{ij}$에 대한 $Loss_f$의 gradient는 아래와 같이 계산될 수 있다(첫 번째 loss).

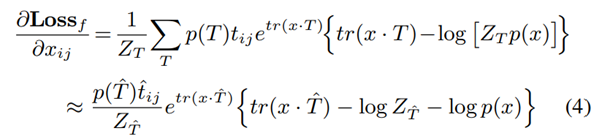
$Z_T=\sum_{x\in X} e^{tr(x*T)}$ 임을 기억하자. 또한, trace에 대한 항들은 위의 식 (2)와 (1)을 참고하자.

이 때, $\hat{T}$는 feature map $x$에 대한 target 템플릿이다.

예를 들면, 주어진 이미지 $I$가 filter $f$의 target category에 속한다면, $\hat{T}=T_{\hat{\mu}}$이다

위에서, $\hat{\mu}=argmax_{\mu=[i,j]}x_{ij}$이다. 즉, feature map 내 가장 활성화된 위치이다.

만약, 이미지 $I$가 다른 categories에 속한다면, $\hat{T}=T^{-}$가 된다.
최초의 학습 에피소드 후에, $\forall T\in \bold{T}\setminus \{\hat{T}\}, e^{tr(x*\hat{T})}\gg e^{tr(x*T)}$ 라는 점을 고려할 때, 위 식 (4)와 같은 근사를 만들 수 있다.

feature map x에서 가장 값이 높은 위치를 중심으로 템플릿 $\hat{T}$를 고르기 때문에 충분히 target template $\hat{T}$에 대해 $tr(x*\hat{T})$를 나머지 template들인 $T$에 대한 $tr(x*T)$보다 크게 만들 수 있다.

$Z_T$가 상당히 많은 양의 feature maps을 사용해 연산되기 때문에, 우리는 $Z_T$를 러프하게 상수($Z_{\hat{T}}$)로 여겨 위 식(4)의 그래디언트를 계산하고자 하였다. 우리는 학습과정동안 점진적으로 $Z_T$의 값을 업데이트한다. 유사하게, 방대한 연산 없이 $p(x)$또한 근사화할 수 있다.

본 연구에서는 학습 과정에서 많은 feature maps를 받을 때 $Z_T$의 값을 근사화하고, 업데이트 하기 위해 feature maps의 부분 집합(혹은 평균)을 사용한다. 유사하게, $p(x)$ 또한 feature maps의 부분집합을 사용해 근사화할 수 있다.

$p(x)\\ =\sum_Tp(T)p(x|T)\\ =\sum_Tp(T){{exp[tr(x*T)]}\over{Z_T}}\\ \approx\sum_Tp(T)mean_x{{exp[tr(x*T)]}\over{Z_T}}$

Determining the target category for each filter: 우리는 각 filter $f$를 target category $\hat{c}$에 할당해야 한다(식 (4)의 그래디언트를 근사화하기 위해). 우리는 간단히 category $\hat{c}$를 갖는 이미지들이 filter $f$를 가장 많이 활성화 할 때, filter $f$를 category $\hat{c}$에 할당한다. 즉, 식으로 나타내면 아래와 같다.

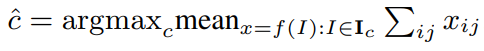
5. Experiments

Three benchmark dataset
Four types of CNNs*
Implementations details

5.1. Experiments

Single-category classification
Multi-category classification*

5.2. Quantitative evaluation of part interpretability

5.2.1 Evaluation metric:part interpretability

• Motion representations for articulated aniamtion에 쓰인 Evaluation metric과 비교할 필요가 있다.

5.2.2 Evaluation metric: location instability

5.2.3 Experimental results and analysis

5.3. Visulaization of filters*

6. Conclusion and discussions*

Note

1. 성능 저하는 얼마나 있는지
2. 후속연구 중 Object detection 연구가 있는지