[개념정리] LRP(Layer-wise Relevance Propagation)

temp·2021년 9월 24일

XAI / Object Detection

목록 보기

11/24

배경

LIME, Filter Visualization와 같은 피처맵 시각화 방식은 모델이 입력 이미지에 어떻게 반응하는 지 각 은닉층을 조사하는 방법이다. 하지만 이는 깊은 은닉 계층일수록 해석력이 떨어지고, 해석자마자 모델을 다양하게 받아들일 소지가 여전히 존재한다.
LRP(Layer-wise Relevance Propagation)은 딥러닝 모델의 결과를 역추적해서 입력 이미지에 히트맵을 출력한다. 히트맵은 블랙박스가 데이터의 어느 곳을 주목하는지 표시할 수 있기 때문에 피처맵 기법보다 블랙박스를 오인할 가능성이 적다. LRP는 이러한 히트맵 방식 XAI 기법 중 가장 대표적인 방식이다.
LRP는 아래와 같이 크게 두 가지 기법으로 혼합되어 있다.

타당성 전파(Relevance Propagation, RP): 특정 결과가 나오게 된 원인을 분해하고, 비중을 분배하는 과정
분해(Decomposition): 타당성 전파를 통해 얻어낸 ‘원인’을 가중치로 환원하고 해부하는 과정

이론

딥러닝 모델은 가중치(weight), 편향(bias), 활성화 함수(activation function) 등으로 이루어진 신경망의 결합이라고 볼 수 있다. 특히 딥러닝 모델은 피처를 연결하고 활성화되는 과정이 비선형적(non-linear)이고 다양한 커널로 매핑되기 때문에 추론하기가 어렵다. 이러한 비선형성을 극복하고 설명성을 부여하기 위해 다양한 기법들이 존재해왔던 것이다.
필터 시각화나 민감도 기법은 딥러닝 모델에서 순 방향으로 진행(feed-forward)하며 데이터 흐름을 관찰하는 기법이다. LRP는 이와 반대로 블랙박스가 분류한 이미지 결과를 역순으로 탐지하며 분해하고, 분해된 요소들이 원본 이미지까지 도달했을 때 원본 이미지에 상대적인 기여도를 표시함으로써 딥러닝 모델을 해석한다. LRP는 딥러닝 모델을 역순으로 탐지하기 위해 분해(Decomposition) 기법을 사용하고, 기여도를 계산할 때는 타당성 전파(Relevance Propagation)을 사용한다. 이 두 가지 기법에 대해서 더욱 자세히 알아보자.

분해(Decomposition)

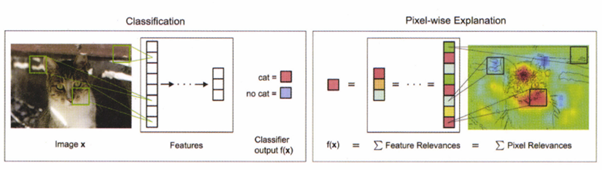
LRP는 히트맵으로 결과를 산출하기 때문에 특정 입력 값의 어떤 부분을 가중해서 이해하고 있는지를 시각화할 수 있다.: Bach, Sebastian, et al. “On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation”

분해는 간단히 말하면 입력된 피처 ‘하나’가 결과 해석에 얼마나 영향을 미치는지 해체하는 방법이다. 예를 들어, 어떤 이미지 $x$ 에서 픽셀 $k$ 가 결과를 도출하는 데 도움이 되는지(+), 해가 되는지(-)를 알아낼 수 있다.
위 그림에서 블랙박스 모델은 이미지를 ‘고양이’로 분류한다. LRP는 이 때 ‘고양이’를 결정하는 데 도움이 되는 영역을 빨간색, 잘못 분류하는 영역을 파란색으로 표시한다.
CNN의 분류 과정(사진의 왼쪽, Classification)에서는 이미지의 픽셀들은 (녹색의 박스로 표시되는) 영역으로 묶인 다음, 피처 하나로 응축돼 은닉층에 전달된다. 이렇게 전달된 은닉층은 또 다른 은닉층으로 전달된다. 마지막으로는 분류 결과(cat or no cat)을 내보낸다.

LRP의 분해 과정(사진의 오른쪽, Pixel-wise Explanation)에서는 $f(x)$ :이미지를 '고양이' 로 예측할 가능성에서부터 딥러닝을 역방향으로 순회하며 각 은닉층의 결과 기여도를 판단한다.

타당성 전파

타당성 전파(Relevance Propagation)는 분해 과정을 마친 은닉층이 결과값 출력에 ‘어떤 기여’를 하는지 타당성을 계산하는 방법이다. 타당성 계산으로 모든 은닉층 내 활성화 함수의 기여도를 계산할 수 있다면, 이미지 $x$ 에서 픽셀 별 기여도를 표시할 수 있다(Pixel Relevances).
해당 과정을 수식으로 먼저 살펴보자.

$f(x)$ : 블랙박스 함수 f가 이미지 x를 입력받아 이미지를 분류할 때의 타당성(relevance)
$V$ :은닉층 벡터
$R_d$ :은닉층 벡터 한 원소의 타당성 점수

라 정의할 때, 이미지 $x$ 에 대한 타당성은 $R_d$ 의 기여도 총합에 근사한다(아래 식).

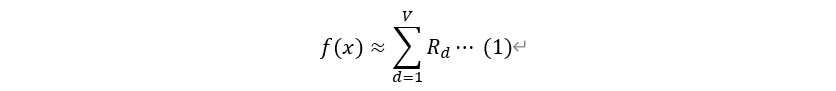
위 식에서 $R_d>0$ 라면 피처 $d$ 가 블랙박스 모델 예측에 긍정적인 영향을 미치는 것이고, $R_d<0$ 일 땐 그와 반대일 것이다.

타당성 전파라는 단어에는 $f(x)$ 로부터 $\sum_{d=1}^{V}R_d$ 를 계산하는 과정과, 특정 은닉층에서 다음 은닉층까지 ‘상대성’을 계산하는 과정을 모두 포함한다.

더 자세히 살펴보면, 어떤 딥러닝 모델 은닉 $l$ 층에 대한 피처 $d$ 의 기여도를 $R_d^{l}$ 라 하자. 즉, 어떤 입력 이미지 $x$ 에 대한 피처(‘픽셀’) $d$ 의 기여도가 $R_d^{1}$ (첫 번째 은닉층 – 입력 이미지)로 표현된다. 하지만 $f(x)$ 와 $R_d^{1}$ 사이에는 수 많은 은닉층이 있기 때문에 가운데에 있는 은닉 층들을 거쳐야 ‘입력 이미지’에 대한 기여도를 알 수 있게 된다(아래 식).

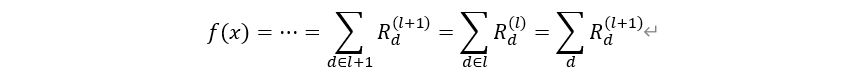
위와 같은 과정을 간단히 3개의 뉴런, 1개의 은닉층을 나타내는 모델로 도식화해보자.

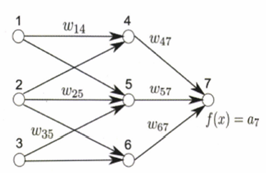
위의 그림이 입력 이미지 $x$ 를 입력 받아 분류를 하기까지의 과정이고,

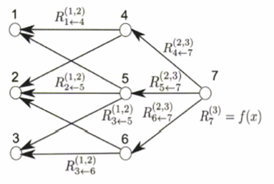
위 그림은 위와 같은 과정을 정확히 반대로 진행하는 과정이다(그림:Bach, Sebastian, et al(2015).

이 때 1번 node에서 4번 node로 이어지는 가중치 $w_{14}$ 와 4번 node에서 1번 node로 이어지는 기여도 $R_{1←4}^{(1,2)}$ )는 방향도 반대이지만, 크기도 반대인데 이는 타당성이 ‘비율’로 정의되기 때문에 값에 제한이 없는 가중치와는 다르다. 또한 가중치는 음의 값도 가질 수 있지만 타당성 계층은 모두 양의 값을 가진다.

본 논문 (Bach, Sebastian, et al. "On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation." ) 에서는 ‘보존 특성(conservation property)’이라는 아이디어를 사용해 (은닉층의) 타당성 계층 간 총합이 일치하게 한다.

가중합

보존 특성을 임의로 나타내면 아래와 같다.

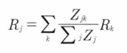
이 때 $j,k$ 는 뉴런으로, 서로 연결되어 있다. $Z_{jk}$ 는 $k$ 뉴런이 보존되도록 $j$ 뉴런이 기여한 비중(가중치 기반, 추후 서술)을 나타낸다.
위와 같이 보존 특성을 가정하면, 은닉층 별 타당성은 아래와 같이 표현할 수 있다.

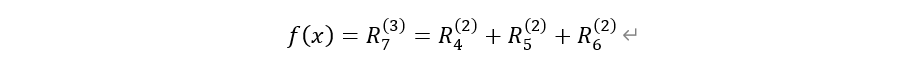
이 때 R은 기여도를 나타낸다. 이를 확장하면

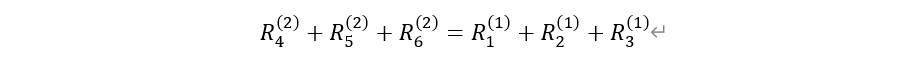
즉, 은닉 계층마다 피처의 타당성(Relevance, R)의 총합이 같다는 것을 알 수 있다.
이 때 각 은닉 피처 하나에 대한 타당성 변수 R을 계산하는 방법은 아래와 같다.

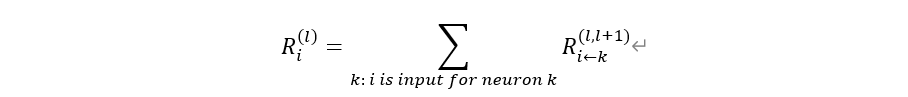
예를 들어, 첫번째 은닉층의 두번째 뉴런은 아래와 같이 계산된다.

또한, 타당성 전파는 방향이 따로 없는데 이는 신경망의 역방향 뿐만 아니라 순방향으로도 구할 수 있다.

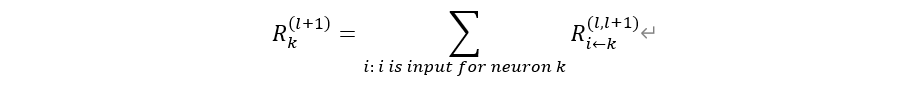
즉, 위 그림의 $R_5^{(2)}$ 의 경우

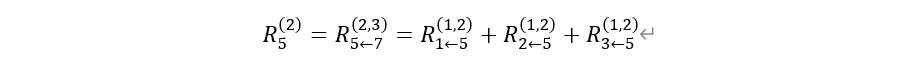
와 같이 구할 수 있다.

이 과정을 통해서 타당성 전파의 간선(edge) 간의 값을 양쪽으로 추론할 수 있다. 궁극적으로 목표하는 것은 $R_{d\in image}^{(1)}$ 이고, 이 상대성은 입력 이미지 다음 레이어의 은닉층 타당성 전파 간선인 $R_{d^{image}\leftarrow d^{hidden}}^{(1,2)}$ 을 계산해 구할 수 있다. 은닉층의 타당성 또한 그 이후의 전파로 알 수 있다.

즉, 정리하면

1. 타당성은 타당성 전파 간선(EDGE)들을 더해서 구할 수 있고
2. 간선은 양방향으로 진행된다.
3. 각 은닉층을 연결하는 간선의 타당성을 계산할 수 있다면, 전체 타당성 상수 R을 계산할 수 있다.

이제, 가장 중요한 타당성 전파 간선( $R_{i\leftarrow k}^{(l,l+1)}$ )을 계산해보도록 하자.

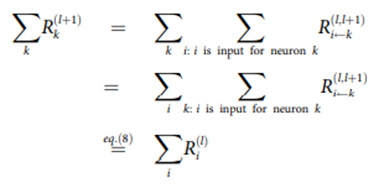
이 때, $R_{i\leftarrow k}^{(l,l+1)}$ 를 정의하기 위한 가장 좋은 방법은 뉴런 $i$ 에서 $k$ 로 갈 때 역할을 하는 $a_i w_{ik}$ 를 이용하는 것이다.
즉,

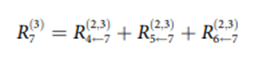
이 식과 유사하게 가중치로 표현하면 아래와 같다.

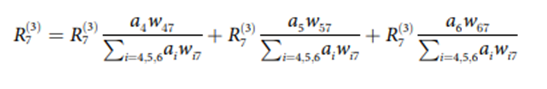
이로부터 직관적으로 아래와 같은 타당성 전파 간선을 표현할 수 있다.

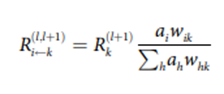
위에서 $i,k$ 는 뉴런이고, 서로 연속적으로 연결되어 있다. 또한 $h$ 는 $k$ 와 연결된 뉴런들로, $i$ 는 $h$ 들 중 한 값을 가질 것이다.

편미분

편미분 ${{\partial f}\over{x_1}}, {{\partial f}\over{x_2}}$ 를 이용해 기여도를 계산 가능하다.

해당 출력 값을 기여도로 분해하기 위해 본 논문은 테일러 급수를 사용했다.
임의의 매끄러운 함수 $f(x)$ 및 실수 $a$ 에 대해 $f(x)$ 의 테일러 시리즈는 다음과 같이 나타낼 수 있다.

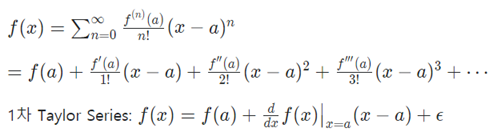
$\epsilon$ : 2차 이상의 항들
${{d}\over{dx}}f(x)|_{x=a}(x-a)$ : relevance score 결정( $x$ 가 변할 때 $f(x)$ 가 얼마나 변하는 지 알 수 있음)
$f(a)=0, \epsilon =0$ 일 때 relevance를 계산할 수 있음.

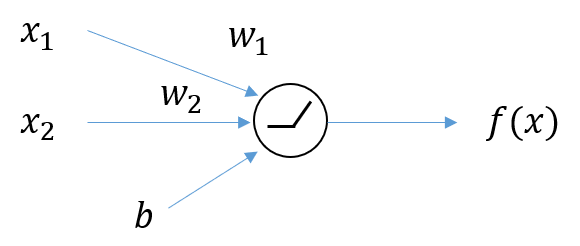
딥러닝에서는 입력이 여러 개이므로 multivariate function에 대한 테일러 시리즈를 이용해야 한다.(여기서 2개)

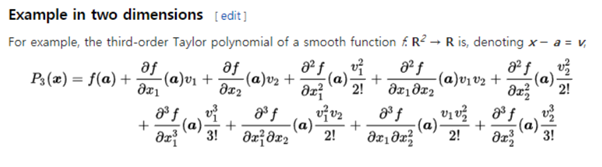
입력이 2차원일 때의 테일러 급수(3차까지).

$f(x)=f(a)+\sum_{p=1}^{d}{{\partial f}\over{\partial x_p}}|_{x=a}(x-a)+\epsilon$

입력이 $d$ 차원일 때 1st order 테일러 시리즈. 이 때, $\sum_{p=1}^{d}{{\partial f}\over{\partial x_p}}|_{x=a}(x-a)+\epsilon$ 은 $x_p$ 가 변했을 때 $f(x)$ 가 얼마나 변하는 지를 나타내주는 항이다. 또한 첫번째 항 $f(a)$ 에 대해 다음이 성립해야 한다.

$f(a)=0$ 의 조건을 만족시켜야 타당성 보존이 이루어짐( $\epsilon=0$ ).

$f(a)=0$ 을 만족 시키는 $a$ 를 찾아 그 근방에서 근사화 한다.

Deep Taylor Decomposition

위에서 아래와 같은 식이 성립함을 알 수 있다.
$f(x)=f(a)+\sum_{p=1}^{d}{{\partial f}\over{\partial x_p}}|_{x=a}(x-a)+\epsilon$

이 때, $f(a)=0, \epsilon=0$ 일 때 relevancies를 계산할 수 있다.

$f(x)=f(a)+\sum_{i=1}^{d}{{\partial f}\over{\partial x_i}}|_{x_i=a_i}(x_i-a_i)+\epsilon$
= $\sum_{i=1}^{d}{{\partial f}\over{\partial x_p}}|_{x=a}(x-a)$
= $\sum_{i=1}^{d}R_i$

즉, 출력을 Relevancy Score만으로 분해하자.

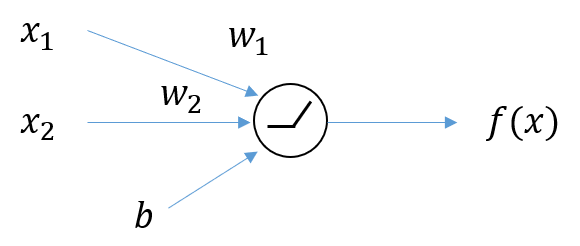
Neural Net에서 $f(x)$ 의 출력값이 나오기 전에 활성화함수로 ReLU를 사용한다고 가정하자. 그러면,
$f(x)=max(0, \sum^{2}_{i=1}w_ix_i+b)$
의 형식으로 나타낼 수 있다.

ReLU함수는 0보다 작은 값의 경우 $f(x)=0$ 을 부여하기 때문에 0보다 큰 경우에 대해서만 계산해야 한다.

이제 $f(x)$ 에 대해 테일러 분해를 하면 아래와 같다.
$f(x)=\sum^{2}_{i=1}w_ix_i+b=f(a)+\sum^{d}_{i=1}{{\partial f}\over{\partial x_i}}|_{x_i=a_i}(x_i-a_i)+\epsilon$

$f(x)=w_1x_1+w_2x_2+b$ 에서 각 원소별로 편미분을 진행해주면
${{\partial f(x)}\over{\partial x_1}}=w_1$ , ${{\partial f(x)}\over{\partial x_2}}=w_2$ 가 나오며, 이 이상의 더 높은 항들에 대해서는 모두 편미분값이 0이 나온다. 따라서, $\epsilon =0$ 이다.
즉,
$f(x)=\sum^{2}_{i=1}w_ix_i+b=f(a)\sum^{2}_{i=1}w_i(x_i-a_i)$
이 때 $a$ 는 테일러 시리즈를 활용해 함수를 근사할 때, 그 시작점 $x=a$ 이다. $f(a)=0$ 의 제약조건을 만족하는 $a$ 를 찾아 대입을 하면 된다.