[개념정리]SHAP(Shapley Additive exPlanations)

A는 이사 갈 집을 구하고 있다. 특정 집의 가치를 판단하는 인공지능을 다운받아서 사용하려고 한다. 이 때, 특정 주택 하나가 주변의 집들보다 집 값이 굉장히 높았다. 하지만, 인공지능은 이 집의 값을 적절하다고 판단한다. 이 때, 이 집의 가격이 합리적이라는 판단을 내린 것에 대해 어떤 근거로 그런 판단을 내렸는지 알 수 있을까? 즉, 범죄율이 낮아서 그런지, 세금 감면 혜택 덕분인지, 그것도 아니면 강가를 끼고 있기 때문인지 알아야만 올바른 분양을 받을 수 있을 것이다.

배경

SHAP는 로이드 섀플리(Lloyd Stowell Shapley)가 만든 이론 위에 피처 간 독립성을 근거로 덧셈(addition)이 가능하게 활용도를 넓힌 기법이다. 즉, 섀플리 값과 피처 간 독립성을 핵심 아이디어로 사용한다.
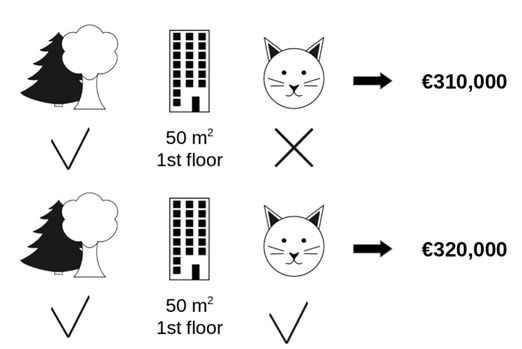
이 때, 섀플리 값은 전체 성과(판단)를 창출하는 데 각 참여자(피쳐)가 얼마나 공헌했는지 수치로 표현할 수 있다. 위의 주택을 예시로 들면, 해당 집에서 강가까지의 거리를 강제로 변경했을 때 집값이 어떻게 변할지 예측한 다음, 변경 전과의 차이를 ‘강가까지의 거리’가 ‘집 값’에 이바지하는 정도라고 추론할 수 있는 것이다.

이는 Feature Importance랑 어떻게 크게 다를까?

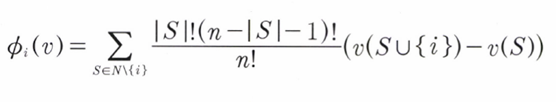
$\phi_i$: $i$ 데이터에 대한 섀플리 값
$n$: 참여자
$S$: 총 그룹에서 $i$번째 인물을 제외한 모든 집합
$v(S)$: $i$번째 인물을 제외하고 나머지 부분 집합이 결과에 공헌한 기여도
$v(S\cup\{i\})$: $i$번째 인물을 포함한(전체)기여도

(고양이의 영향을 알아보기 위해서, 고양이를 제외한 집합의 모든 경우의 수를 살펴 가중 평균을 계산하는 것이 핵심이다)

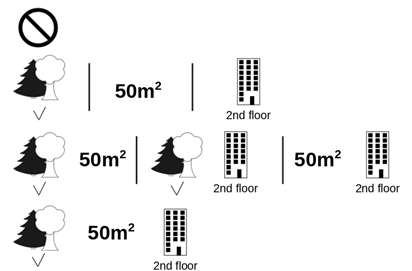
예를 들어, 피처가 4개($x_1,x_2,x_3,x_4$)인 모델이 있다고 해보자. 이 때, 전체 모델에 대해서 {$x_2$} 피처 하나가 기여한 가치 S는 아래와 같이 계산할 수 있다.

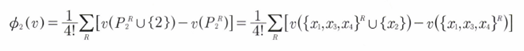
즉, 섀플리 값은 모델이 표현할 수 있는 모든 조합과 피처 $x_2$를 제외한 피처의 조합을 빼서 평균을 낸다. 예를 들어 {$x_2,x_4$} 피처가 기여한 가치 $S$는 $\phi_2(v)$와 $\phi_4(v)$를 더한 값이다.

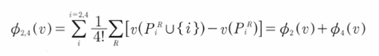
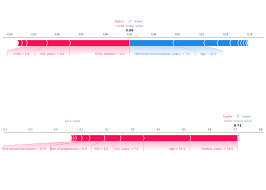
SHAP는 모델의 출력을 각 피처의 기여도로 분해한다. 다음은 SHAP가 처음 등장한 논문에 있는 그림이다.

Lundberg et al(2018), Consistent individualized feature attribution for tree ensembles.

위의 그림에서 SHAP는 모든 가능한 피처 순서쌍에 대해서 샘플링하고 평균 값을 계산한다(E[y]). 오른쪽 화살표들은 원점으로부터 f(x)가 높은 예측 결과를 낼 수 있게 도움을 주는 요소고, 왼쪽 화살표는 예측에 방해되는 요소이다. 섀플리 값은 음수일 수도 있는데, 이 때는 특정 피처가 예측에 부정적인 역할을 미치고 있다고 해석할 수 있다.

---

SHAP를 더 알아보기에 앞서서, 피처 중요도(Feature Importance)나 부분 의존성 플롯(PDP)에 대해 알아보고 넘어가자.

1. 피처 중요도 : 예측에 가장 큰 영향을 주는 변수를 퍼뮤테이션(Permutation)하며 찾는 기법. 피처의 변화가 예측에 주는 영향력을 계산함으로써 피처 영향력을 측정하지만, 퍼뮤테이션의 정도와 에러에 기반한 추정 한계 때문에 알고리즘 실행 시마다 중요도가 다를 수 있다. 또한, 피처 중요도는 ‘피처 간 의존성’을 간과한다(피처 간 상관관계가 존재하는 모델은 사용을 지양해야 한다).

2. 부분 의존성 플롯(PDP): 관심 피처를 조정한 값을 모델에 투입해 예측값을 구하고 평균을 낸다. 부분 의존성 플롯은 3차원까지의 관계만 표시할 수 있는 한계를 가진다. (4차원 이상의 플롯은 할 수 없어 결과가 왜곡될 수 있다)

단, SHAP는 이와 다르게 피처 간 의존성까지 고려해서 모델 영향력을 계산한다(SHAP가 계산한 모든 피처 영향력의 합은 1).
또한 피처의 결측을 시뮬레이션해야 하기 때문에 계산 시간이 오래 걸리고, 샘플 계산량을 줄이면 계산 시간은 빨라지더라도 오차의 분산이 커진다. 또한 SHAP는 학습된 모델에 대해서만 설명할 수 있으므로, 피처의 추가와 삭제가 빠른 모델을 설명하기에는 적합하지 않다.

피처 중요도, 부분 의존성 플롯, SHAP는 모두 model-agnostic(모델에 상관 x) 하지만 모두 다른 방법으로 계측하고, 알고리즘마다 장단점이 명확하다.

예를 들어, 집값을 예측하는 피처들 몇 개가 서로 의존적이라면 피처 중요도는 피처 영향력을 잘못 계산할 수 있다. 비교하고자 하는 피처가 많아지면 특정 피처의 변화에 따른 집값의 영향은 시각화할 수 없고, 피처 영향력이 과대 평가될 위험 또한 있다. SHAP는 집값을 결정하는 기준이 어떻게 배분되는지 균형있게 해석한다. 단, 시간이 오래 걸리고 새로 나온 이상치(혼자만 집 값이 높다던가..)의 등장에 허술한 해석을 내놓을 가능성이 있다. 또한 1. 피처중요도와 2. PDP는 모델의 관점에서, SHAP는 데이터 하나에 대한 설명을 구한다.

---

SHAP 논문 보충

기존의 LIME기법 들과 다르게, SHAP는 결과가 결정적이라는 것 외에도 이상적인 특징이 몇 가지 더 있다

1. Consistency: 항상 결과가 일정
2. Multicollinearity: 서로 영향을 미칠 가능성을 고려
3. Feature Importance: 음의 영향력 또한 고려할 수 있다.

A. Additive Feature Attribution Method Definition

복잡한 딥러닝 모델을 보다 간소화하여 설명력이 좋은 모델을 최적화하는 모든 기법

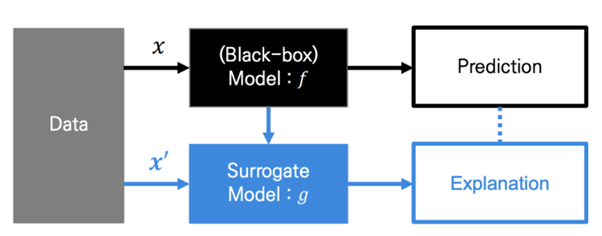
기존의 LIME에서 다루었던 내용과 거의 유사하다.

즉, 복잡한 모델 $f(x)$대신 해석 가능한 모델인 $g(x')$로 해석하는 것이 목표. $x$는 복잡한 모델에 특화되어 있는(입력으로 받는) 복잡한 데이터이다. 이의 해석을 위해 $x'$라는 간단화된 변수를 사용하고자 하며, Simplified input $x'$는 $x=h_x(x )$라는 mapping function에 의해 정의된다.
$z'\approx x'$라는 가정을 통해, $z'\in \{0,1\}^{M}$으로 표현되며($1$:모델에 포함된 특성, $0$: 모델에 배제된 특성)
$g(z')\approx f(h_x(z'))$가 되도록 설명가능한 모델 $g(x)$를 학습한다.

(이하 논문 내 내용, 생략)

결국, Feature Attribution에 가장 중요한 요소는 아래와 같은데,

1. Local Accuracy
   
2. Missingness
   
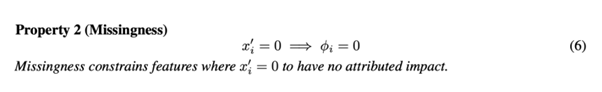
3. Consistency
   

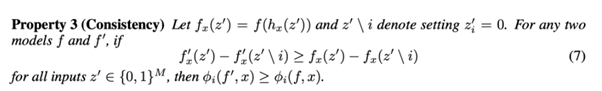
위의 조건들을 만족시키는 SHAP의 식은 아래와 같다.

즉, 여기서의 SHAP는 Shapley Value를 사용하여 Additive Method를 만족시키는 설명 모델이라고 볼 수 있다.

SHAP

SHAP : Shapley Value의 조건부 기대값

$f_x(z')=f(h_x(z'))=E[f(z)|z_S]$

오른쪽 화살표(파란색)은 원점으로부터 $f(x)$가 높은 예측 결과를 낼 수 있게 도움을 주는 특성이며, 왼쪽 화살표(빨간색)은 $f(x)$ 예측에 방해가 되는 요소이다.

SHAP는 Shapley value (데이터 한 개에 대한 설명, $Local$)을 기반으로, 데이터 셋의 ‘전체적인 영역’에 대한 해석이 가능하다($Global$)
모델 $f$의 특징에 따라, 계산법을 달리하여 빠르게 처리한다.

1. Kernel SHAP : Linear LIME + Shapley Value

2. Tree SHAP : Tree Based Model

3. Deep SHAP : Deeplearning based model

   여기서는 단순히 KernelSHAP에 대해서만 살펴보자

   

1. $x_i,Feature value$ 에서 조합을 생성한다. 단, $z_i={0,1}^{M}으로 사용하는 Random feature coalitions를 사용
2. $z_i'=1$인 경우 actual feature value에 mapping, $z_i'=0$인 경우 random sample value로 mapping
3. $z_i'$를 본래의 feature space로 mapping 시킨 다음($h_x (z_i')=z$), $f(z)$에 적용함으로써 예측 값을 얻을 수 있다(본래의 복잡한 모델과 같이). 즉, Local Surrogate model에 대한 설명 변수는 $0$과 $1$로 이루어진 값이 되며, 반응 변수는 이에 대한 예측 값이 된다.
4. 각 Feature 조합마다 SHAP Kernel $π_x(z')$를 적용하여 Weight를 준 다음, 위에서$L(f,g,π_x')$식을 최소화 함으로써 linear model $g(z')=\phi_0+\sum_{i=1}^{M}\phi_iz_i'$를 적합시키고(설명하기 쉬운 모델이므로)
5. 위의 식에서 $\phi_i$=Shapley Value : $i$번째 특성을 대변하는 가중치를 반환한다.

SHAP 실습

SHAP 실습

Ref.

SHAP - in velog.io/@tobigs_xai
XAI, 설명 가능한 인공지능, 인공지능을 해부하다 (안재현. 2020)
Seminar - 고려대학교 DMQA 연구실 (korea.ac.kr)
A Unified Approach to Interpreting Model Predictions (nips.cc)