Paper: https://arxiv.org/pdf/2003.14080.pdf
Code: https://github.com/Panda-Peter/image-captioning.
0. Abstract
최근에는 visual recognition과 vqa task에서 Bilinear Pooling을 많이 활용하고 있습니다(BiP).
BiP는 multi-modal input에 대해 order interaction을 모델링하는 방법입니다.
그럼에도 불구하고, 그런 BiP가 image captioning을 위한 attention model에도 효과적인지 다루는 연구는 거의 없었습니다.
본 논문에서 저자들은 BiP만을 활용하여 visual information을 선택적으로 captilize하거나, Multi-modal 추론을 행하는 X-Linear Attention Block을 제안합니다.
높은 order, (혹은 무한대의 order), 의 feature interaction는 X-Linear Attention Block을 여러 개 쌓음으로써 완성됩니다(혹은 Exponential Linear Unit을 활용하거나).
ELU는 파라미터가 필요 없습니다.
이런 X-Linear attention blocks을 활용한 image encoder, sentence decode를 활용해서 X-Linear Attention Networks을 구축할 수 있었고, intra- & inter- modal 간 정보 흐름을 잘 엮을 수 있었습니다.
CIDEr metric으로 측정했을 때 132% 가량의 성능 향상이 있었다고 합니다.
1. Introduction
이미지 캡셔닝 방법론들에 대거 채택됐던 Encoder-Decoder 구조 중 초기 모델은 (일부 모델을 제외하고) Vision과 Language을 독립적으로 여겨 두 모달 간에 상호작용을 좀처럼 하지 않았습니다.
초기 단계에 두 모달(Text, Image) 간에 Early Fusion을 하지 않음(Attention이라든지..).
이와 다르게, Attention 관련 아키텍처들은 decoder(즉, 문장 생성)의 각 hidden state를 조건(즉, query)으로 받아, encoder(즉, 이미지 이해)에서 공간 정보들에 특정 가중치를 부여함(즉, key-value)으로써, decoding 과정에 가이드라인을 부여합니다.
아래 그림을 봅시다.
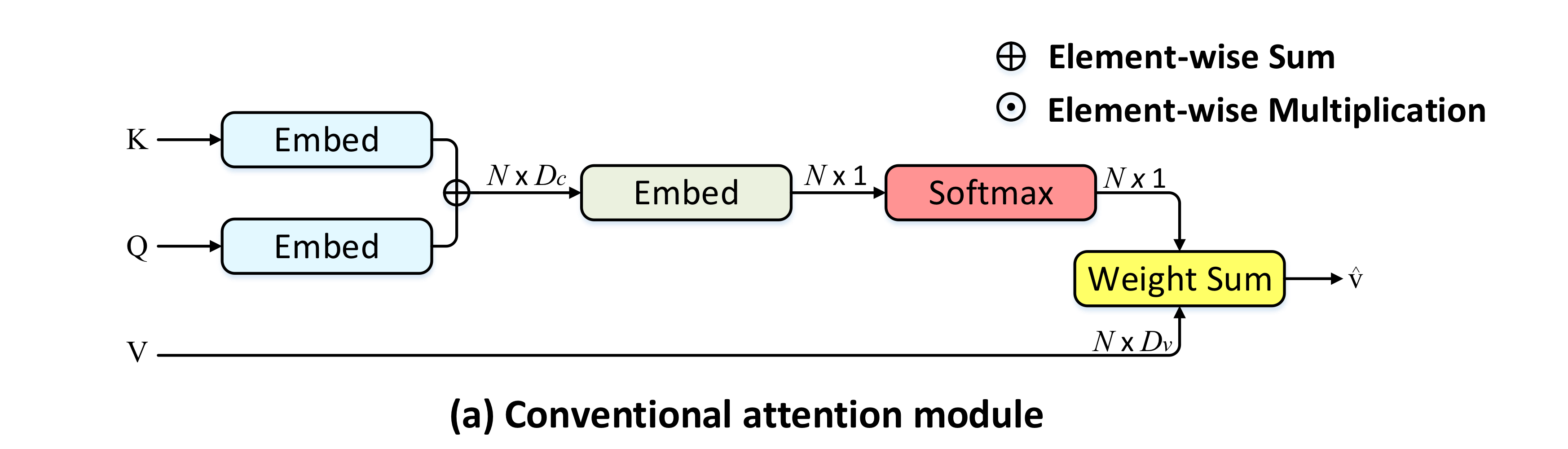
위 그림은 전통적인 attention 방법을 보여줍니다.
decoder에서 query를 받고, encoder에서 key를 받아 유사도를 구한 다음, 마찬가지로 encoder에서 value를 받아, 구해놓은 유사도를 이용해 가중합을 구하게 됩니다.
하지만, 위의 전통적인 어텐션 방법은 단지 order의 feature interaction만을 행하게 되고, 효율이 떨어진다고 합니다.
즉, 이미지 캡셔닝에 필요한 복잡한 multi-modal reasoning 능력을 크게 제한하게 됩니다.
반면, 저자들이 제안한 X-Linear attention block을 봅시다.
이론적인 내용은 후술하기로 하고, 결론적으로 위의 외적(~BiP)를 이용해서, 저자들은 order의 interaction을 수행하고, 이로부터 image features와 hidden states 간 joint representation을 추론할 수 있게 됩니다.
이런 Attention Block을 Encoder 내에서 self-attention(intra-modal)처럼 적용하고, 후에 Encoder-Decoder 간에 co-attention(inter-modal)처럼 적용함으로써 두 모달(이미지, 텍스트) 간에 높은 수준의 상호작용을 수행할 수 있게 됩니다.
2. Related Work
2.1. Image Captioning
- pass
2.2. Bi-linear Pooling
BilinearPooling(BiP)는 두 feature vector 간에 외적을 수행하는 연산입니다.
원소끼리만 곱하게 되는 linear pooling과는 다르게, 가능한 모든 원소 pair 간 상호작용이 일어나기 때문에 일종의 order interaction이라고 볼 수 있습니다.
최초에는 fine-grained visual recognition task에서 장점을 보였으며, 후에는 연구 *"Compact bilinear pooling. In CVPR, 2016."에서 pooling의 성능은 유지하면서 고 차원의 bilinear pooling feature를 (비교적 저차원인) 수천 차원으로 압축하는 방법을 제안하게 됩니다.
이를 VQA와 같은 Multi-Modal task에 적용하기도 했구요.
다만, 위에서 제안한 Compact bilinear pooling은 너무 복잡한 연산을 필요로 하기 때문에, Linear mapping과 Hadamard Product를 이용하는 flexible low-rank bilinear pooling구조가 제안되기도 했습니다.
J in-Hwa Kim, Kyoung-Woon On, Woosang Lim, Jeonghee
Kim, Jung-Woo Ha, and Byoung-Tak Zhang. Hadamard
product for low-rank bilinear pooling. In ICLR, 2017.
3. X-Linear Attention Networks(X-LAN)
봄 단락에서 저자들은 spatial bilinear attention, 그리고 channel-wise bilinear attention을 이용해 order feature interaction을 포착하는 X-Linaer attention block을 제안합니다.
또한 이를 인코더-디코더 네트워크에 통합한 구조도 제안했습니다.
3.1. Conventional Attention Module
전통적인 어텐션 구조 먼저 봅시다.
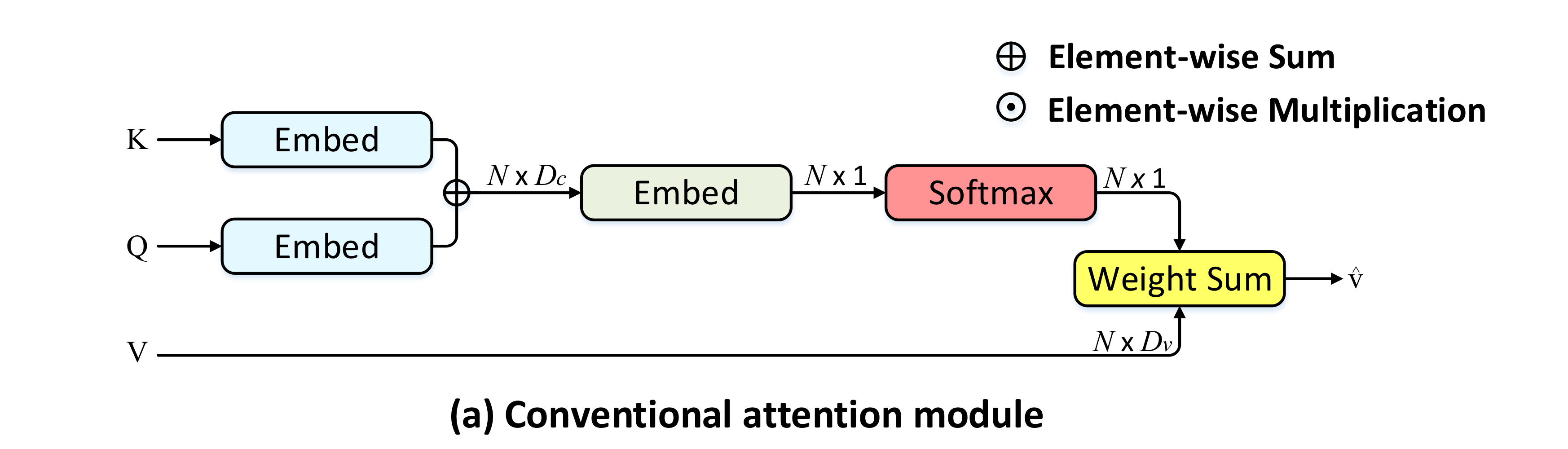
Captioning에서 전통적인 어텐션 구조는 문장 생성에 쓰일 salient image regions을 선택적으로 attend하게끔 학습됩니다.
일반적으로, decoder 내 time step 에서, Query 가 주어졌을 때, Key 에 대한 attention distribution 를 얻게 됩니다.
: Decoder의 Hidden state(Query)
: Encoder의 Image Features(Key, 개)
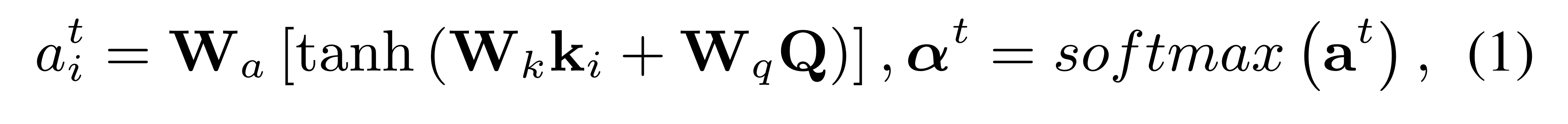
: 임베딩 행렬
즉, 개의 Key(Local Image Feature)에 대한 개의 attention weight 를 얻게 됩니다.
특히, key와 queyr 간에 element-wise sum을 이용해서.
(additive attention)(dot-product 아님)
위와 같이 Attention Weight 구한 후 이를 가중치로, image feature 를 값으로 여겨 attended image feature 를 구하게 됩니다.
즉, Local Image Feature를 따라서 가중합을 하기 때문에 이를 spatial attention weight로 표현하게 됩니다.
(일반적으로 Key와 Value는 같은 벡터입니다).
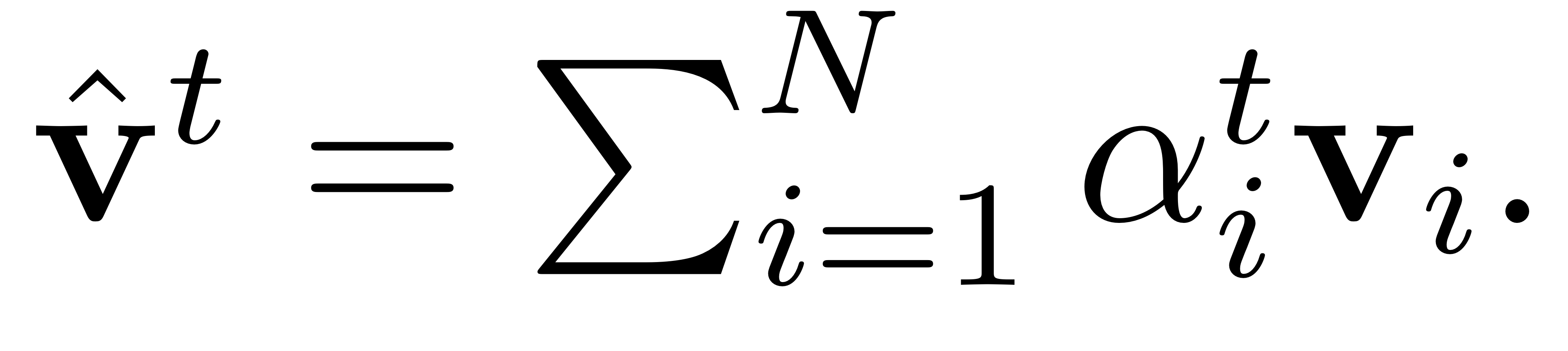
3.2. X-Linear ATtention Block
위의 전통적인 어텐션 방법은 원소 간 제대로 된 상호작용을 이끌어내지 못하기 때문에, 이를 개선하기 위해 bilinear pooling을 이용하게 되었고, 패턴 인식, VQA task에서도 좋은 결과를 보였습니다.
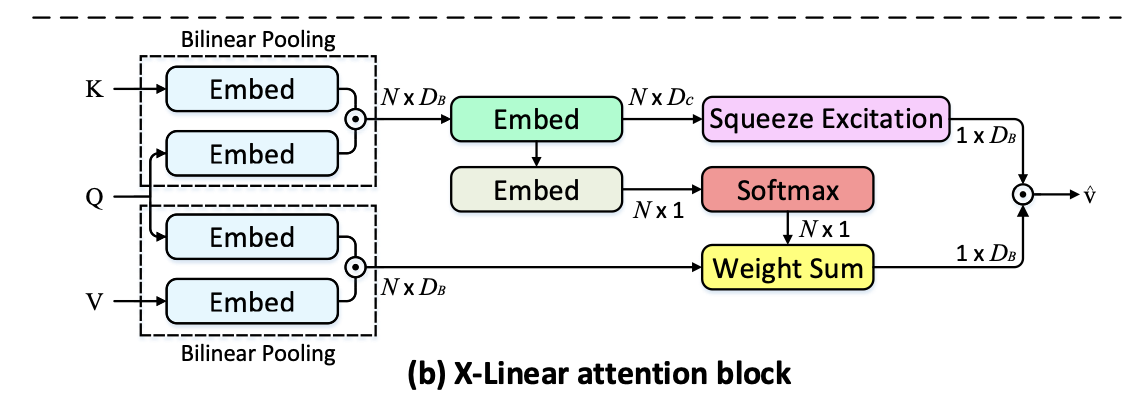
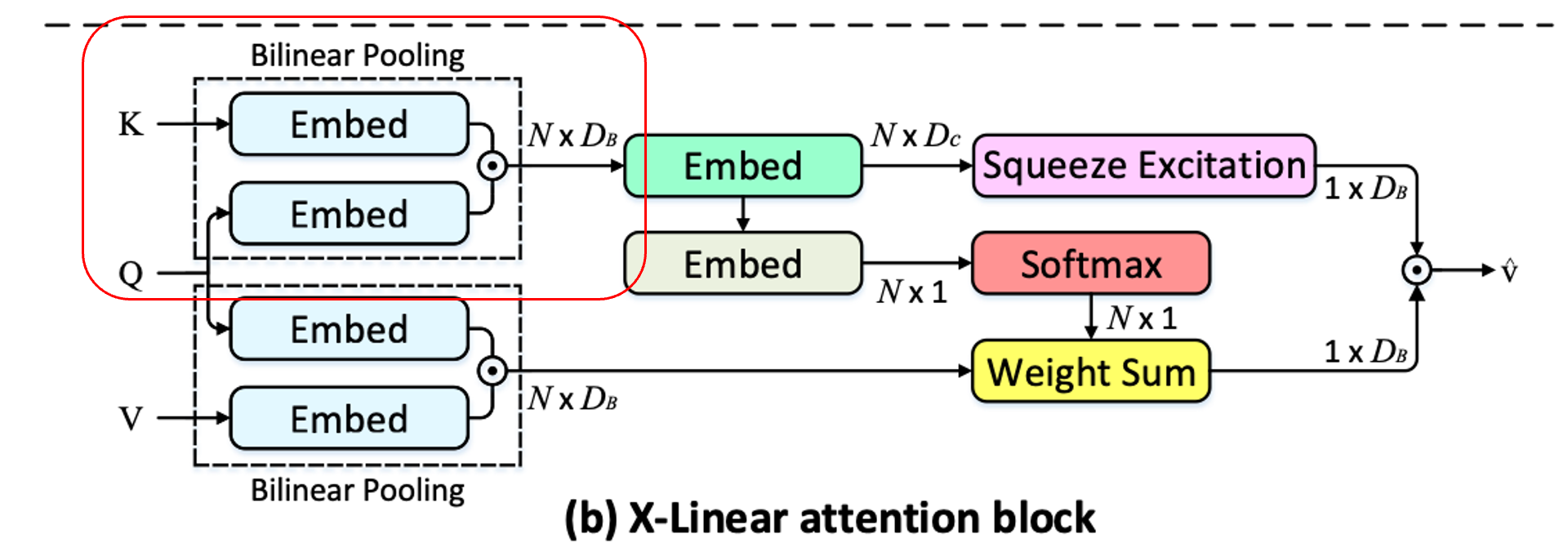
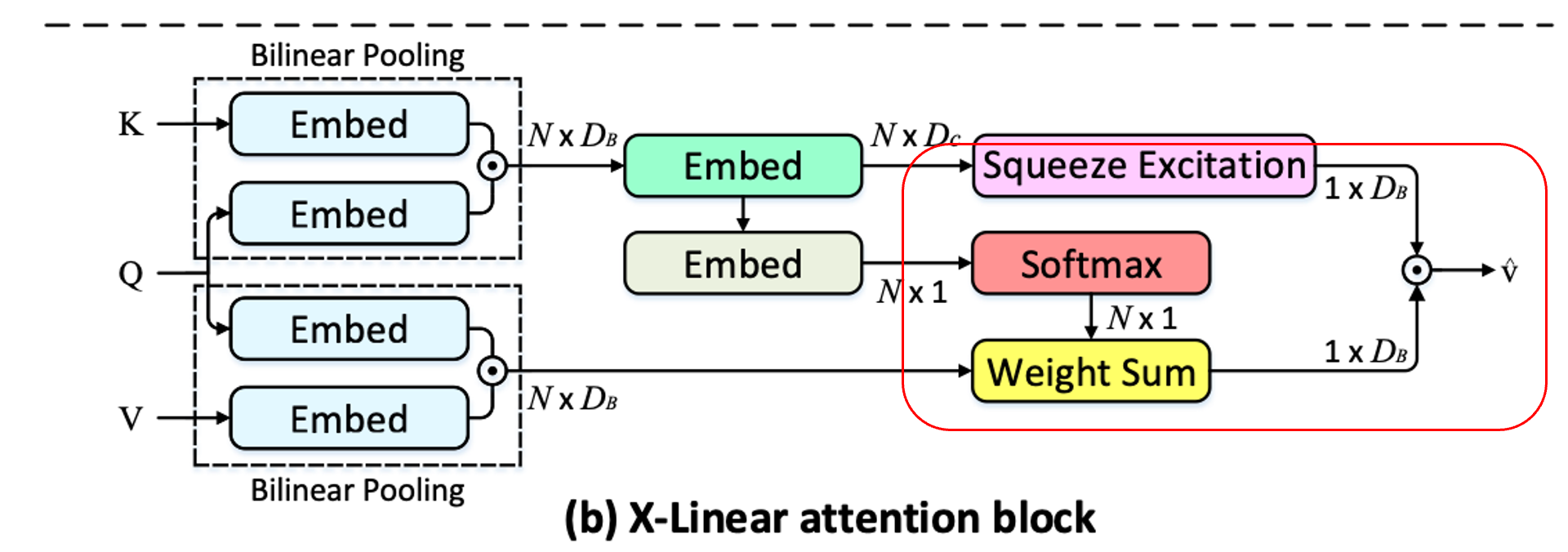
이런 BiP만을 이용해 attention module을 대체하기 위한 방법으로 저자들은 X-Linear attention block을 제안했으며, 그림은 아래와 같습니다.
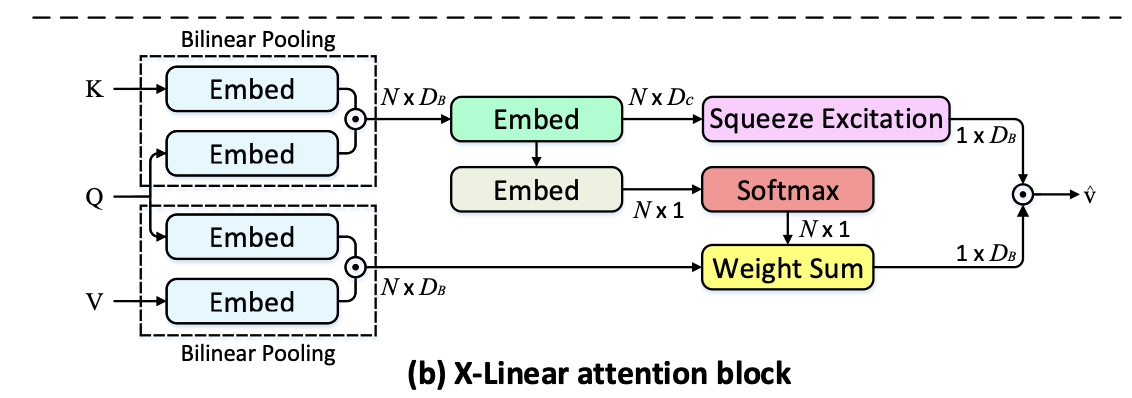
이 결과로 나오게 되는 최종적인 attended vector 는 intra-, inter-modal feature 간에 고차원적인 상호작용을 기반으로 하기 때문에 더욱 많은 정보를 담고있다고 볼 수 있습니다.
Notation
- query , key 간에 얻은 joint bilinear query-key representation(의 원소).
특히, 식 전개에 있어서 공간(spatial)에 의존하는 기호, 채널(channel)에 의존하는 기호 와, key에 의존하는 , value에 의존하는 등을 구분해 살펴보면 비교적 이해하기 쉽습니다.
- Query 와 각 key 에 대해 low-rank blinear pooling을 수행해 joint bilinear query-key representation 을 얻습니다.
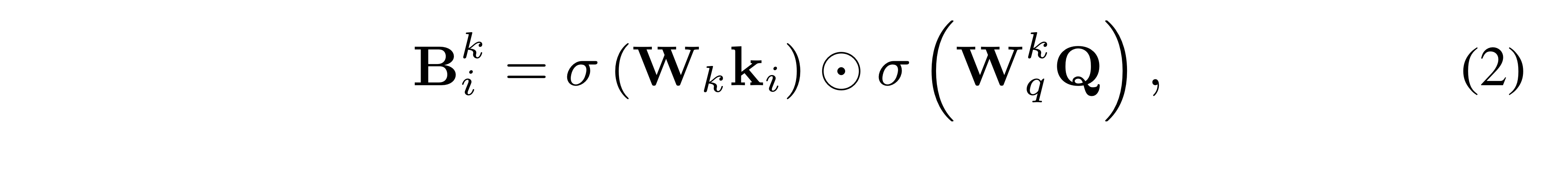
는 각각 , , 즉 Key의 번째 원소 와 Query 를 차원으로 맞춰주는 임베딩 매트릭스입니다.
(나머지 기호는 ReLU, Element-wise multiplication..)
위의 low-rank blinear pooling으로 얻은 결과인 는 query와 key 사이에 order의 feature interaction 정보를 지니고 있습니다.
Query의 임베딩 행렬이 key에 의존하는 로 표현하는 이유는 단순히 뒤에 나올, value에 의존하는 와 구분해주기 위함입니다.
그 후, 모든 query-key representation 를 고려함에 따라, 두 종류의 attention distribution을 얻을 수 있게 됩니다.
- spatial information
- channel-wise information
spatial information
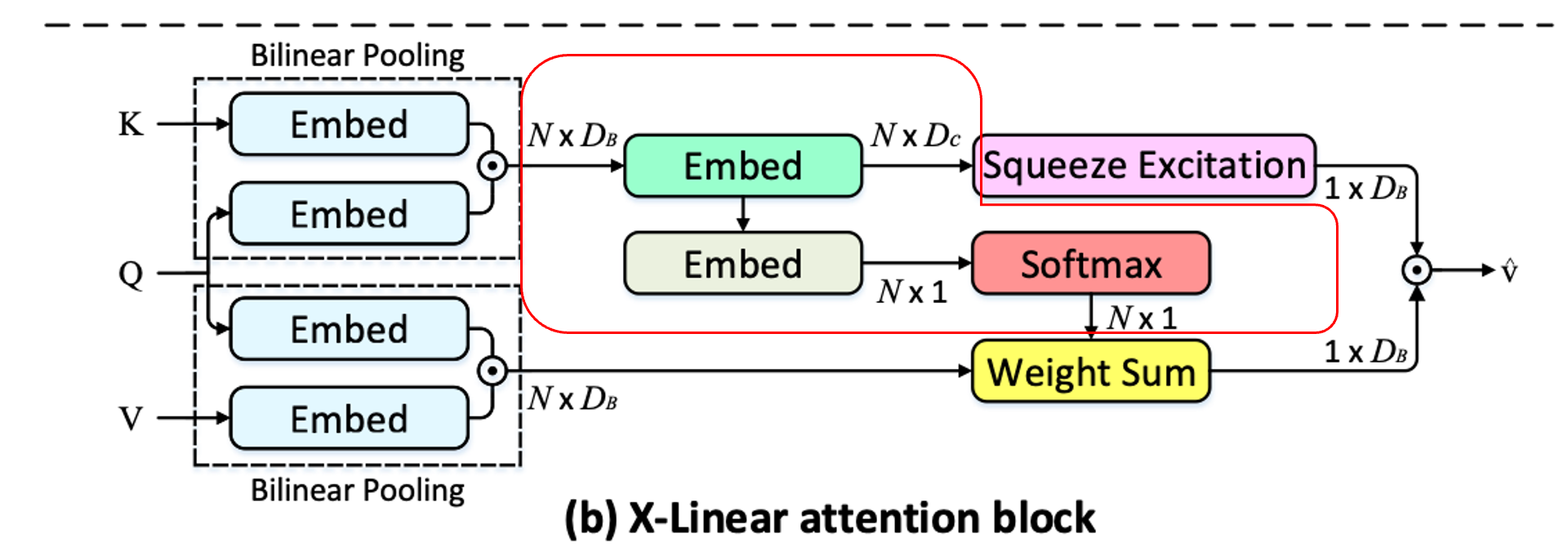
아래와 같이 두 개의 임베딩 를 이용해서 각각의 query-key representation에 맞는 attention weight를 얻게 됩니다.
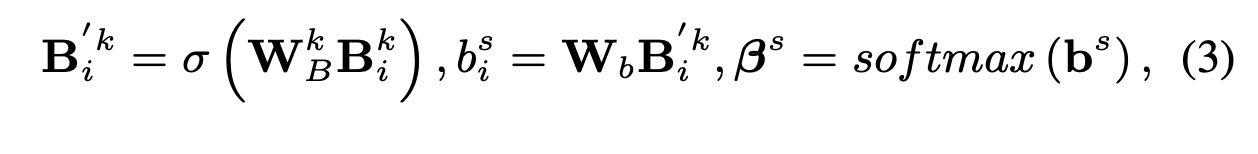
, ,
: transformed bilinear query-key representation
spatial information(spatial attention distribution)을 다루기 때문에 최종적으로는 얻게 되는 차원 는 "normalized spatial attention distribution for each key/value pair"가 되게 됩니다.
사실 굳이 linear matrix를 1개만 사용하는 것 대신에 + (비선형) + 처럼 2개를 이용해 spatial attention weight 를 얻어야될 필요가 있나 싶지만, 앞 쪽 두 개의 식을 통해 얻은 임베딩 벡터는 바로 밑에 서술할 Squeeze Excitation을 위해서도 쓰이기 때문에 겸사겸사 쓰였다고 이해하면 될 거 같습니다.
(비선형 층을 하나 더 쌓는 것도 나쁘진 않은 선택이어서 일 수도 있고..)
channel-wise information
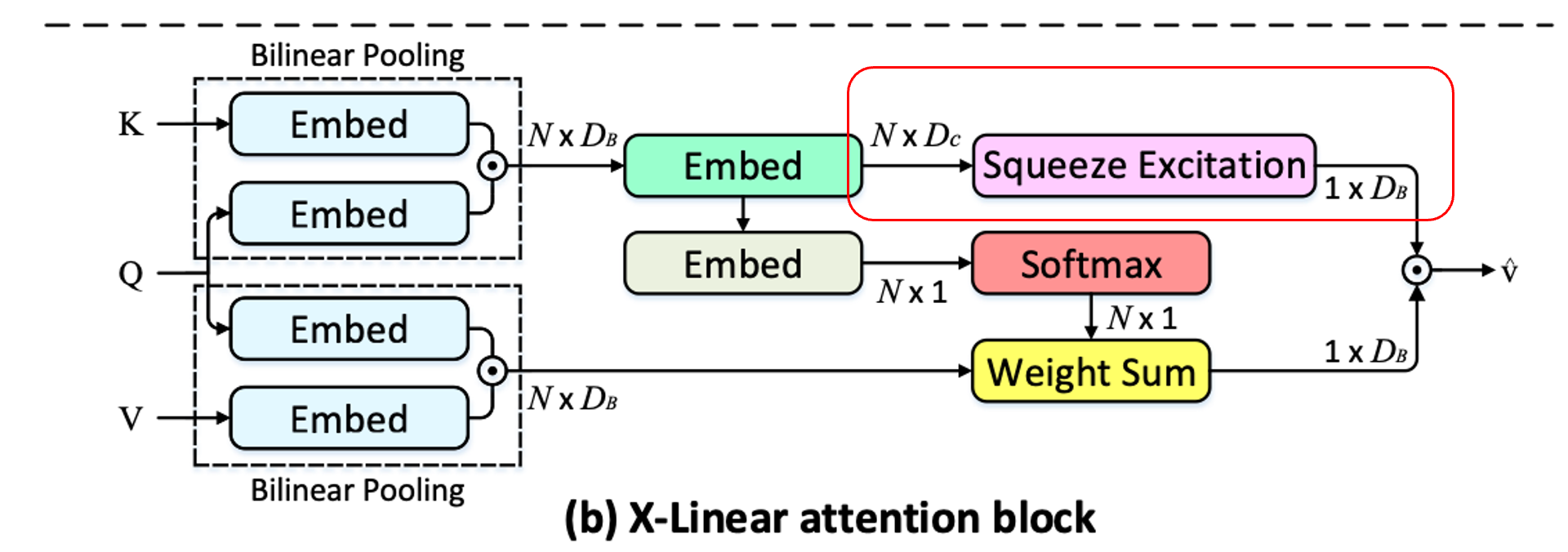
그 외에도, 위 식에서 얻은 transformed bilinear query-key representations 에 대해 squeeze-excitation operation을 수행해, channel-wise attention measurement를 얻게 됩니다.
구체적으로 말하면, (1) squeeze operation은 average pooling을 이용해 모든 transformed bilinear query-key representation을 (시퀀스를 따라) average pooling해줌으로써 global channel descriptor 를 얻게 됩니다.
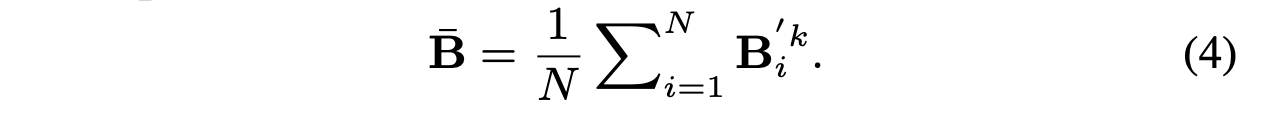
즉, 공간정보에 구애받지 않으며, 개의, 차원의 Key와 차원의 Query에 대한 bi-linear pooling 정보를 차원에 담고 있는 벡터
그후, (2) excitation operation은 위에서 얻은 global channel descriptor 에 대해 self-gating 매커니즘을 적용해줌으로써 channel-wise attention distribution 를 얻게 됩니다.
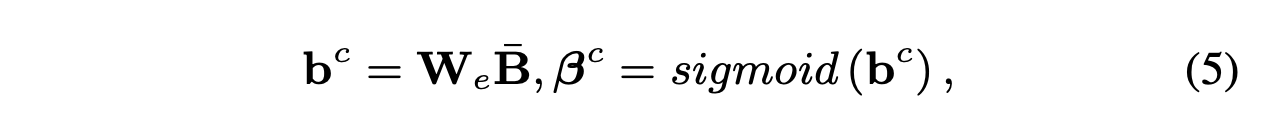
는 위의 spatial information 단계에서 를 구할 때 차원으로 줄어든 벡터를 다시 차원으로 늘려줄 수 있게끔 차원을 갖습니다.
그 후 시그모이드에 통과시켜줌으로써 사이의 값을 갖는 차원의 벡터가 되며, 이로 인해 (하단부 Fusion 단계에서 얻을) value에 대해 attention weight를 부여할 수 있는 벡터 를 얻을 수 있게 됩니다.
Fusion
마지막으로, 위에서 얻은 spatial & channel-wise bilinear attention들과, 새롭게 얻을 query와 value 간 enhanced bilinear values(식6의 두번째 줄)를 통합함으로써(식6의 첫번째줄) 최종적인 attended value feature 를 얻게 됩니다.
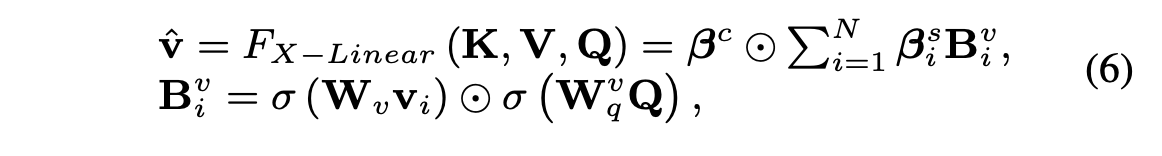
,
즉, 에서는 spatial-attention이 적용되며(합이 1인 attention distribution), 에서는 channel-wise attention이 적용됩니다(합이 1은 아닌, attention(gated) distribution.
Default : ,
Extension with higher order interactions
이를 쌓아서 더 높은 order를 갖는 interaction을 행할 수 있게 됩니다.
(생략)
우선 알고 싶었던 부분은 X-Linear Attention block 이었기 때문에 이하 내용들은 생략.