- 전체보기(273)
- algorithm(70)
- leetcode(50)
- AI(22)
- C++(9)
- LLM(8)
- python(6)
- Java(6)
- NLP(4)
- IntelliJ(4)
- Markdown(4)
- Computer Vision(3)
- github(3)
- PyTorch(3)
- cpp(2)
- CV(2)
- BERT(2)
- json(2)
- ML(2)
- DL(2)
- langChain(2)
- NP-hard(2)
- Signed Distance Fields(2)
- docker(2)
- transformer(2)
- Octree(1)
- Vision Transformer(1)
- iterator(1)
- maven(1)
- Linear Algebra(1)
- security(1)
- lambda(1)
- algirhtm(1)
- Sliding Window(1)
- Tail Recursion(1)
- vector(1)
- DETR(1)
- beamer(1)
- binary tree(1)
- Time Series(1)
- B+TREE(1)
- Game of Life(1)
- gradle(1)
- class(1)
- anaconda(1)
- huggingface(1)
- Foundation model(1)
- QUADTREE(1)
- Automata(1)
- Sustainable AI(1)
- regex(1)
- Off-by-one error(1)
- RundPod(1)
- graphics(1)
- VS Code(1)
- latex(1)
- notion(1)
- Continual Learning(1)
- bitwise(1)
- leetecode(1)
- leecode(1)
- RL(1)
- data(1)
- 코드테스트(1)
- Regular Expresssion(1)
- adaptive learning(1)
- Quatization(1)
- multi-task learning(1)
- reinforcement learning(1)
- computer engineering(1)
- Multi-Label(1)
- Multi classification(1)
- B-tree(1)
- SDK(1)
- bigdata(1)
- dynamic programming(1)
- data structure(1)
- Coding(1)
- 3D(1)
- vscode(1)
- git(1)
- Imbanaced Data(1)
- GPT(1)
- Computer Sicence(1)
- math(1)
- 선형대수(1)
- API(1)
- visual studio(1)
- dataset(1)
- ViT(1)
- rag(1)
[AI] 실험 Cache
같은 계산을 중간 결과를 저장해 두고, 같은 계산을 반복하지 않는다.머신러닝 실험에서는 다음 항목에서 사용될 수 있고, 이런것들이 매번 반복되면 매우 비효율적이다.데이터 로딩임베딩 계산cross-validation 결과hyperparameter 평가 결과다음의 문제 상
[AI] Stratified
Stratified(계층화)는 데이터 클래스 비율은 그대로 유지하면서 데이터를 나누는 방법이다.보통, train / validation / test 분할이나 cross-validation에서 사용한다.전체 데이터 100개이면서, 클래스 분포가 아래와 같다면,Class
[AI] Hyperparameter Tuning : 실험
Hyperparameter 모델의 성능은 하이퍼파라미터(hyperparameters) 선택에 크게 좌우된다. 아래는 머신러닝·딥러닝에서 가장 널리 사용되는 대표적인 튜닝 방법들이다. Grid Search (격자 탐색) 개념 미리 정의한 하이퍼파라미터 후보 값들의
[AI] Hyperparameter
머신러닝 모델을 학습 할 때, 여러 값들을 설정한다.이 설정값들은 파라미터와 하이퍼파라미터 두 종류로 나눌 수 있다.하이퍼파라미터(hyperparameter) : 사람이 미리 정해주는 값파라미터(parameter) : 학습을 통해 자동으로 배우는 값모델이 데이터로부터
[AI] Ablation Study
전체 파이프라인을 고정하고, 제안하는 요소를 하나씩 제거하거나 단순화하여 성능 변화를 확인한 번에 한 가지만 바꾸기 (나머지 고정)Full 모델이 항상 포함돼야 한다성능뿐 아니라 비용(시간/메모리)도 같이 분석하여 설득력 증가각 요소가 “필수인지” 보여주는 정석적인 방
[AI] 논문 비교 실험
보통 논문 비교하는 부분 작성할 때, 어떻게 가져다가 쓸까? 내가 구현한 코드의 특정부분만 교체하는걸까??비교 실험헤서 reviewer가 보는건 이 성능 차이가 정말 제안하는 방법덕분인가? 인지이다. 그래서 다른 부분들은 최대한 고정하고 비교하고 싶은 요소만 최소한으로
[AI] Pytorch Derivative, Partial derivative and Gradient
$$f'(x) = \\lim\_{h \\to 0} \\frac{f(x+h) - f(x)}{h}$$함수 $f(x) = x^2$에 대해:$$\\frac{df}{dx} = 2x$$$x=3$일 때:$$\\frac{df}{dx}\\bigg|\_{x=3} = 2 \\cdot 3
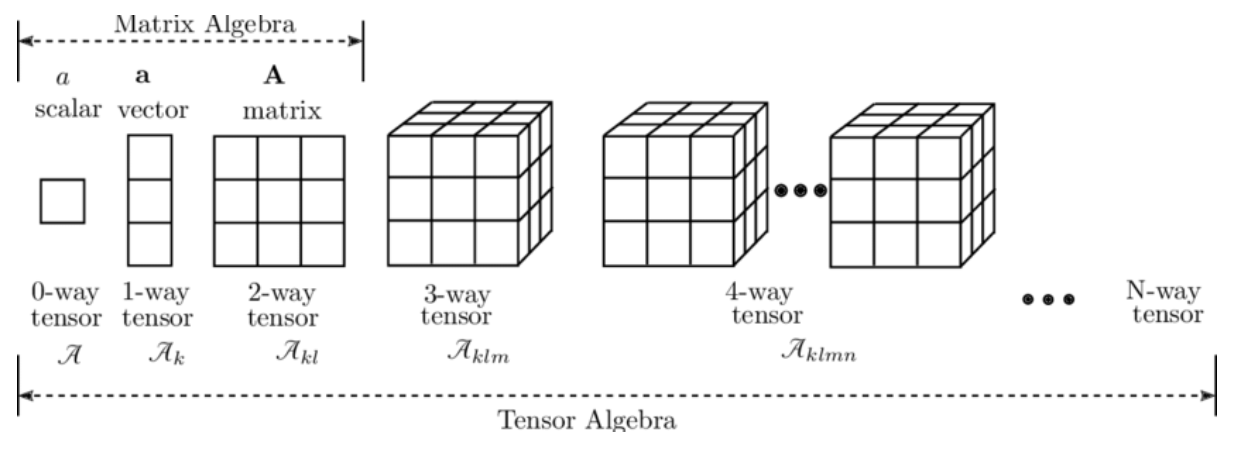
[AI] Pytorch with Scala, Vector, Matrix
torch PyTorch의 텐서(tensor) 연산을 위한 핵심 모듈 차원별 구조 스칼라 (0차원 텐서) 단일 숫자 값 Vector (1차원 텐서) 숫자들의 1차원 배열 Matrix (2차원 텐서) 숫자들의 2차원 배열 Tensor (3차원 이상) 더 높은 차원
[AI] Experiment Setting
가장 중요한 부분고정해야 하는 것:weight initdata shuffleclient samplingaugmentation매번 새로 생성 ❌split 결과를 파일로 저장train.txt / test.txt 식으로 고정num_workers > 0 이면 꼭 필요함❌예시O
[Remote] Cursor & VS Code 의 SSH Remote 설정
linux 서버 구축하고 사용하고 있었는데, GUI로는 너무 느려서 VS Code와 Cursor로 ssh remote 연결해서 사용하기로했다기본적으로 사용 방법이 같아서, 동일하게 실행해서 editor만 본인이 원하는 대로 설정하면 된다!openssh-server 설치
[ML] Bi-Encoder and Cross-Encoder
Encoder는 어떤 정보를 압축 하거나, 변형하여 특정 형태로 만들어 내는 것을 말함ML에서는 다양한 Encoder가 있고, Bi-Encoder와 Cross-Encoder 가 있음질문과 문서를 각각 따로 인코딩질문 → 0.2, 0.8, 0.1, ... 벡터1문서A
[NLP] Tokenizer
BPE, WordPiece, Unigram(=SentencePiece Unigram) 세 가지 토크나이저를 같은 코퍼스, 같은 문장으로 비교BPE vs WordPiece vs Unigram 비교자주 등장하는 쌍을 계속 합쳐 나감접두사 \`여러 후보 중 가장 확률 높은
[NLP] max_length vs. token?
Text(input) : "인공지능은 정말 재미있어요!"max_length: 15글자tokens: 약 8-12개 (모델마다 상이)
[AI] K-fold 교차 검증(K-fold cross-validation)
K-fold 교차 검증은 모델의 일반화 성능을 신뢰성 있게 측정하는 중요한 표준 도구머신러닝에서 데이터셋을 K개의 하위 집합(폴드)으로 나누어 반복적으로 학습과 평가를 수행하는 대표적인 검증 기법이다. 전체 데이터를 K개로 나눈 뒤, 각 폴드가 한 번씩 검증 세트로 사
[AI] Macro vs. Micro metrics
정의: 모든 토큰을 하나로 합쳐서 계산토큰 예시: 계산 방식: 전체 TP, FP, FN을 합산 후 계산특징: 빈도가 높은 클래스(예: O)의 영향이 큼전체적인 모델 성능을 반영데이터 불균형에 민감용도: 전체적인 모델 성능 평가공식:정의: 각 클래스별로 계산한 후 평균토
[NLP] NER 측정 방법(Token-level or Entity level)
Token-level F1: 각 토큰(단어)별로 라벨이 맞는지 확인Entity-level F1: 전체 엔티티 단위로 완전히 맞는지 확인문장: "김철수는 서울에서 삼성전자에 다닌다"정답 라벨:모델 예측:전체 토큰: 8개맞은 토큰: 6개 (김, 서울, 삼성, 전자, 나머지
[NER] BIO Tagging
BIO Tagging은 개체명 인식(NER)이나 시퀀스 라벨링에서 개체의 시작과 내부를 구분해 문장의 구조를 기계가 이해할 수 있도록 도와주는 방법자연어 처리(NLP)에서 토큰 단위로 개체(entity)의 범위를 표시하는 대표적인 방식이름 그대로 B–I–O 세 가지 태
[AI] Loss function
모델이 예측한 값과 실제 정답 사이의 차이를 수치고 계산하는 함수값이 작을수록 모델이 예측을 잘 했다는 의미이며, 이 값을 최소화하도록 학습하는 것을 최적화(=optimization)라고 함 회귀: MSE, MAE, Huber, Log-Cosh분류: Cross Ent
[NLP] NER(Named Entity Recognition, 개체명 인식)
- NER은 문장에서 사람, 장소, 조직, 시간, 숫자 등 \*\*의미 있는 단위(개체, Entity)\*\*를 찾아내고 분류하는 작업- "이 문장 속에서 중요한 이름이나 값은 뭐지?"를 기계가 알아보게 하는 것문장: - \*\*"스티브 잡스는 1976년에 애플을 공동
[AI] Bayes' Rule
어떤 사건의 사전 확률(사건이 일어나기 전 우리가 아는 확률)을, 새로운 증거가 관찰된 후에 사후 확률로 갱신하는 방법$$P(A \\mid B) = \\frac{P(B \\mid A) \\cdot P(A)}{P(B)}$$$P(A)$: 사건 $A$의 사전 확률 (증거를
