기본 레이어 이해하기 시리즈

1. Linear Layer 이해하기
2. Convolution Layer 이해하기
3. Pooling Layer 이해하기
4. Deconvolution Layer 이해하기

Embedding

Embedding : 어떤 위상(位相) 공간에서 다른 위상 공간으로의 동상 사상(同相寫像).

쉽게 말해서 매핑(mapping)한다는 얘기다. 즉, 임베딩 레이어는 데이터를 1대1 대응이 가능한 다른 형식으로 바꾸는 일을 한다. 주로 자연어처리에서 사용하지만, 꼭 NLP가 아니더라도 의미적 유사성을 구분하기 위한 수단으로 사용되는 경우가 많다.

그럼 도대체 뭘 어떻게 바꾸는지 알아보자.

희소 표현 Sparse Representation

Sparse Representation, 흔히 희소 표현이라고 부르는 방식은 벡터의 특정 차원에 의미나 단어를 직접 매핑하는 방법이다. 일견 정확도가 높은 방법 같아 보이지만 상당히 비효율적이다. 당장 동음이의어나 다의어를 어떻게 처리할 것인지 생각해보면 문제가 뭔지 바로 알 수 있다.

변환하려는 언어가 표음문자를 사용하는지 아니면 표의문자를 사용하는지에 따라 성능도 바뀔 테고, 무엇보다 특정 차원에 1대1 매핑을 하면 나머지 차원은 대부분 0의 값을 갖는 희소 행렬이 되므로 자원을 효율적으로 쓸 수 없게 된다.

그래서 분산 표현 이라는 방법을 사용한다.

분산 표현 Distributed Representation

희소 표현은 표현하려는 단어 N개만큼의 차원을 갖기 때문에 임베딩 벡터의 차원 수가 변동하지만 분산 표현은 임베딩 차원 크기를 고정해서 사용한다. 분산 표현은 희소 표현처럼 특정 차원이 특정한 의미를 갖는다는 가정을 하지 않는다.

대신 분산 표현이라는 이름에서 알 수 있듯이 표현하려는 단어가 여러 개의 차원들이 나타내는 속성들의 합으로 구성돼 있다고 가정한다. (일반적으로 임베딩 차원 크기는 512 또는 256 정도를 사용한다.)

사실 분산 표현의 아이디어는 상당히 직관적이고 경험적이다. 예를 들어 '사랑'이라는 단어는 어떤 속성들로 표현될 수 있을까? 연인, 가족, 아가페, 성욕, 순수, 열정 등 여러 가지 속성으로 나타날 수 있을 것이다. 그리고 우리는 맥락에 따라 단어를 구성하는 속성이 바뀐다는 것을 알고 있다. 연인간의 사랑과 가족간의 사랑이 다른 것처럼.

분포 가설

분산 표현은 이처럼 단어가 가지는 속성이 맥락에 따라 바뀐다는 아이디어에서 출발한다. 이걸 분포 가설이라고 한다. 정확히는 동일한 맥락에서 여러 번 출현하는 단어는 비슷한 의미를 가진다는 가설이다.

쉽게 말해서 '사랑'을 표현하고 싶을 때, 연인, 가족, 순수, 열정 등의 속성이 어느 차원에 있는지는 모르지만 사랑이라는 단어가 쓰인 맥락을 살펴보면 어떤 의미로 쓰였는지 (사랑이라는 단어가 어떤 속성들로 구성돼 있는지) 추론할 수 있다는 의미이다. 인간이 맥락을 읽는 방법과 상당히 유사하다.

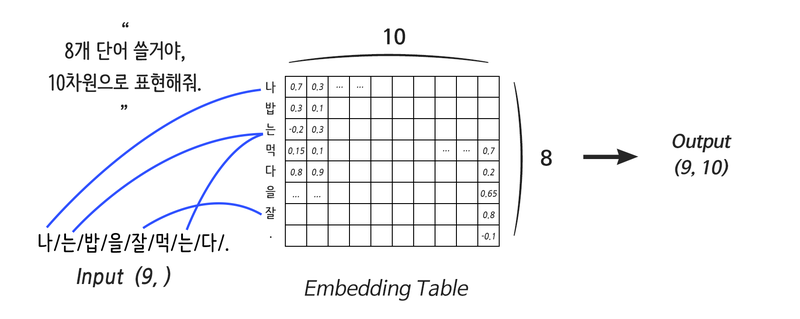
분산 표현은 N개의 단어를 K개의 차원을 가진 벡터로 표현한다. 여기서 K가 바로 Embedding size이다. 벡터로 나타냈기 때문에 코사인 유사도를 활용해 각 단어끼리의 유사도를 비교할 수 있고, 결과적으로 적합한 alignment를 찾아낼 수 있다.

원 핫 인코딩

그럼 (N, K) 모양의 행렬 벡터에 어떤 값을 넣어야 할까? 가장 먼저 생각나는 방법은 원 핫 인코딩이다. 특정 단어가 있냐 없냐를 0, 1로 표현하면 임의의 시퀀스를 하나의 벡터 표현으로 변환할 수 있다.

import tensorflow as tf
import numpy as np

vocab = {
    "i": 0,
    "need": 1,
    "some": 2,
    "more": 3,
    "coffee": 4,
    "cake": 5,
    "cat": 6,
    "dog": 7
}

sentence = "i i i i need some more coffee coffee coffee"
# 위 sentence
_input = [vocab[w] for w in sentence.split()]  # [0, 0, 0, 0, 1, 2, 3, 4, 4, 4]

vocab_size = len(vocab)

one_hot = tf.one_hot(_input, vocab_size)
print(one_hot.np())

위 코드의 출력 결과는 아래와 같다.

[[1. 0. 0. 0. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0.]
 [0. 0. 0. 0. 1. 0. 0. 0.]
 [0. 0. 0. 0. 1. 0. 0. 0.]
 [0. 0. 0. 0. 1. 0. 0. 0.]]

그런데 잘 생각해보면 원 핫 인코딩은 앞에서 언급한 희소 표현과 다를 바 없다. n번째 차원에 n번째 단어를 매핑하는 것과 똑같기 때문이다.

선형 변환으로 데이터를 집약하자

희소 행렬의 문제는 의미 없는 값(0)이 많다는 데서 기인한다. 그러니 그 값을 없애버리면 해결할 수 있을 지도 모른다. 그리고 우리는 데이터를 집약시키는 방법을 이미 알고 있다. 바로 선형 변환이다.

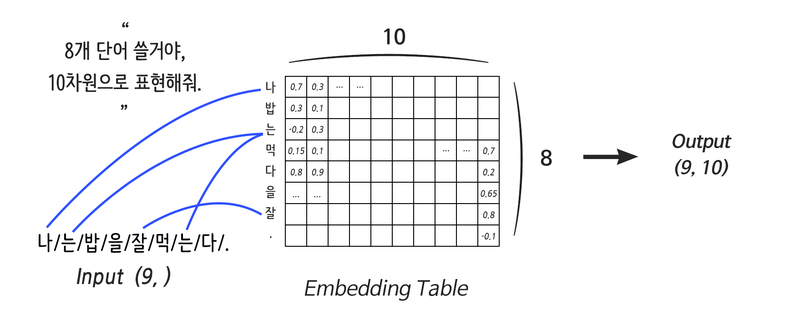
사실 위에서 살펴본 그림에 이미 힌트가 숨어 있었다. 잘 보면 나라는 벡터는 0 또는 1이 아니라 실수값을 가지고 있다. 이런 값은 어떻게 얻을 수 있을까?

# 2차원 분산 표현
distribution_size = 2   

linear = tf.keras.layers.Dense(units=distribution_size, use_bias=False)
one_hot_linear = linear(one_hot)

print("Linear Weight")
print(linear.weights[0].numpy())

print("\nOne-Hot Linear Result")
print(one_hot_linear.numpy())

위에서 원 핫 인코딩한 데이터를 선형변환 레이어에 집어넣어보자.
결과는 다음과 같다.

Linear Weight
[[ 0.36055934 -0.77369654]
 [-0.6315373   0.7412032 ]
 [-0.08681113  0.23452878]
 [-0.13938296  0.39862263]
 [-0.6865345  -0.43795004]
 [-0.5737966  -0.3680002 ]
 [ 0.2757082   0.09362817]
 [-0.24853444 -0.02777416]]

One-Hot Linear Result
[[ 0.36055934 -0.77369654]
 [ 0.36055934 -0.77369654]
 [ 0.36055934 -0.77369654]
 [ 0.36055934 -0.77369654]
 [-0.6315373   0.7412032 ]
 [-0.08681113  0.23452878]
 [-0.13938296  0.39862263]
 [-0.6865345  -0.43795004]
 [-0.6865345  -0.43795004]
 [-0.6865345  -0.43795004]]

0과 1로 이루어진 희소 행렬이 실수 값을 가진 벡터로 변환되었다. 또한 출력된 결과값을 보면 특정한 값이 반복적으로 나타나고 있는데 이는 위에서 지정한 단어장의 인덱스 배열과 동일한 패턴을 보인다. 즉, 희소 행렬에서 [0, 0, 0, 0, 1, 2, 3, 4, 4, 4]에 해당하는 행을 읽어오는 것과 같다.

텐서플로우에서는 다음과 같이 구현할 수 있다.

# 단어 인덱스를 지정
some_words = tf.constant([[3, 57, 35]])
print("Embedding을 진행할 문장:", some_words.shape)

# input_dim = 표현할 시퀀스의 단어 수
# output_dim = 출력할 임베딩 벡터의 차원 수
embedding_layer = tf.keras.layers.Embedding(input_dim=64, output_dim=100)

print("Embedding된 문장:", embedding_layer(some_words).shape)
print("Embedding Layer의 Weight 형태:", embedding_layer.weights[0].shape)

출력 결과는 다음과 같다.

Embedding을 진행할 문장: (1, 3)
Embedding된 문장: (1, 3, 100)
Embedding Layer의 Weight 형태: (64, 100)

임베딩은 미분이 불가능하다

말 그대로 임베딩은 단순한 1대1 매핑 작업이기 때문에 미분이 불가능하다. 미분이 불가능하다는 말은 '일반적으로는' 학습이 불가능하다는 뜻이므로, 임의의 레이어를 통해 출력된 결과를 임베딩 레이어에 연결할 수 없다.

따라서 임베딩 레이어는 input 데이터에 직접 연결되어야 한다.

그래도 학습은 가능하다

학습이 불가능하다는 것은 레이어 단위의 네트워크 내에서 그렇다는 거고, 임베딩 방법론적인 측면에서의 학습은 충분히 가능하다. 당장 본 글에서는 원 핫 인코딩을 사용했지만 ELMo나 Word2Vec 같은 임베딩 방법론적인 측면에서의 학습방법은 아주 많다.

또한 일반적인 딥러닝 네트워크에서도 임베딩 레이어의 출력값을 가지고 가중치를 업데이트할 수 있다.