
PS를 위한 Berlekamp-Massey Algorithm과 그 Python 구현
Berlekamp-Massey Algorithm (BMA) 유한체 $$\mathbb F_q$$ 위에서 작동한다. 동차 선형 점화 수열 $$s_n$$이 주어지면 해당 수열을 생성하는 $k$차 동차 선형 점화식을 반환하는 알고리즘이다. 시간 복잡도는 $$\mathcal O (N^2)$$이다. 주어진 수열을 순회하며 연산한다. > 본 글에서 다루는 알...
[나만 보는 정리노트][르베그 적분 시리즈] 08. 리만-르베그 보조정리
리만 르베그 보조정리는 다음과 같다. >만일 함수 $$f$$가 구간 $$(-\infin , \infin)$$에서 르베그 적분 가능하면 $$\displaystyle\lim{\omega\rarr \infin}\int^\infin{-\infin}{f(t)e^{-i\omeg
[나만 보는 정리노트] 확률 측도
확률공간 $$(\\Omega, \\mathcal{F}, P)$$는 공간 전체의 측도 $$P(\\Omega)=1$$인 측도공간을 말한다.확률론에서는 측도론에서와 다른 여러 용어들을 사용하는데,확률공간의 점들의 집합 $$\\Omega$$는 표본공간이라고 한다.확률공간의 가
[나만 보는 정리노트][르베그 적분 시리즈] 07. 수렴 정리
집합 $$X$$ 위에서 함수열 $${fn}$$이 함수 $$f$$에 균등수렴한다는 것은 수식으로 다음과 같이 나타낼 수 있다.$$\\forall \\epsilon >0,\\,\\exist N\\in\\N\\quad s.t.\\, n\\geq N \\Rarr \\displ

[나만 보는 정리노트][르베그 적분 시리즈] 06. 르베그 적분의 우월성
이상 적분이 아닌 일반적인 경우에 르베그 적분은 리만 적분의 상위호환이다.즉 유계함수 $$f$$가 리만 적분 가능하면 르베그 적분도 가능하다.리만 적분은 유계함수 $$f$$가 $$a. e.$$ 연속일 때 가능한 반면, 르베그 적분은 그렇지 않아도 가능하다.리만 적분 가
[나만 보는 정리노트][르베그 적분 시리즈] 05. 르베그 적분 정의
저번 시간에 대충 르베그 적분이 무엇인지는 알고 넘어갔다.이번 시간에는 지시 함수와 단순 함수를 이용하여 르베그 적분을 정의하는 과정에 대하여 알아보자.지시 함수 $$1_A(x)$$는 $$1_A(x)=\\begin{cases} 1\\quad x\\in A\\ 0 \\q
[나만 보는 정리노트][르베그 적분 시리즈] 04. 르베그 적분의 개념적 이해
르베그는 1926년 5월 코펜하겐에서 강의 도중 다음과 같이 말했다 :
[나만 보는 정리노트][르베그 적분 시리즈] 00. 측도
측도가 무엇인지 알기 위해 우선 $$\\sigma$$-대수에 대해 알아야 한다.집합 $$\\Omega$$의 부분집합들을 원소로 하는 집합 $$B$$가 아래 조건을 만족할 때 $$B$$를 $$\\sigma$$-대수라고 정의한다.$$\\varnothing \\in B$$$
[나만 보는 정리노트][르베그 적분 시리즈] 03. 르베그 측도
르베그 측도에서는 전체 집합의 길이를 가산개로 분할된 부분 집합들의 길이의 합으로 정의한다.물론, 당연하게도 구간 $$a, b$$의 길이는 $$b-a$$로 정의한다.르베그 측도 역시 르베그 외측도 $$\\lambda^:\\mathcal{P}(\\R)\\rarr \\le
[나만 보는 정리노트][르베그 적분 시리즈] 02. 리만 적분
집합 $$P={x0, x_1, x_2, \\cdots,x_n}$$이 $$a=x_0<x_1<x_2<\\cdots<x_n=b$$를 만족할 때 $$P$$를 구간 $$a, b$$의 분할이라고 한다. 분할 $$P$$는 구간 $$ a, b$$를 $$\[x_0
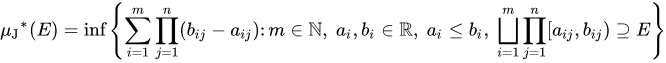
[나만 보는 정리노트][르베그 적분 시리즈] 01. 조르당 측도
조르당 측도는 리만 적분을 정의하기 위해 필요한 측도이다.특정 영역의 넓이를 측정하고 싶다고 할 때, 영역을 포함하는 단위 사각형들의 넓이의 합의 하한이 조르당 외측도이고, 영역에 포함되는 단위 사각형들의 넓이의 합의 상한이 조르당 내측도이다. 하한은 $$\\inf
[PS 일지] 2024-01-07
DP 문제 해결✔ 13976 | Platinum 5 | 타일 채우기 2ㄴ 타일 채우기에서 구했던 점화식을 분할 정복 거듭제곱으로 활용하기만 하면 되는 문제.골드 랜덤 디펜스 ✔ 10830 | Gold 4 | 행렬 제곱 ㄴ 분할 정복을 이용한 행렬 제곱의 기초 문제. ✔
