- 전체보기(70)
- 딥러닝(27)
- 인공지능(26)
- 파이썬(24)
- 넘파이(21)
- 머신러닝(18)
- 판다스(12)
- 배열(12)
- 리스트(11)
- pandas(11)
- 인공신경망(9)
- 객체(7)
- 글쓰기(7)
- 데이터(6)
- 생각(6)
- 수학(6)
- 쓰기(6)
- python(5)
- 기하(5)
- 인생(5)
- 작문(5)
- dataframe(5)
- 미적분(5)
- 경사하강법(5)
- 편미분(5)
- 행렬(5)
- AI(4)
- 클래스(4)
- 데이터프레임(4)
- 함수(4)
- 독서(3)
- 빅데이터(3)
- ML(3)
- 신경망학습(3)
- 손실함수(2)
- 선형회귀(2)
- 퍼셉트론(2)
- 인덱스(1)
- 역사(1)
- 비지도학습(1)
- 모듈(1)
- 파라미터(1)
- axis(1)
- 방향미분(1)
- 그룹화(1)
- 공부(1)
- 사이킷런(1)
- 경제(1)
- xlxs(1)
- 행동변화(1)
- 학습(1)
- 지도학습(1)
- 선형대수(1)
- 강화학습(1)
- sqld책(1)
- gradient(1)
- 디지털(1)
- 시리즈(1)
- 2차원 배열(1)
- 미분(1)
- sqld독학(1)
- 관성끊기(1)
- SQLD(1)
- series(1)
- csv(1)
- 컬럼(1)
- SQLD수험서(1)
- 계획(1)

2026 동계 모각코 - 6회차 (결과)
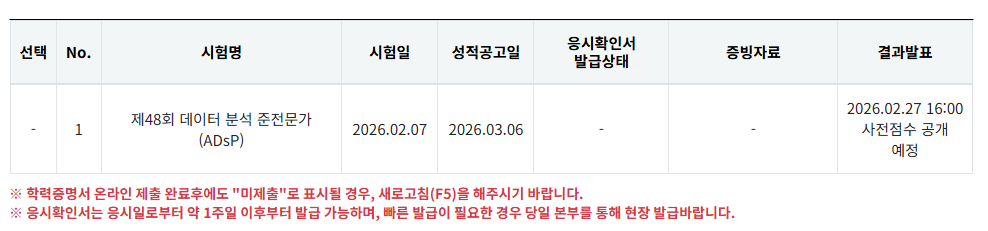
부제 : 2026 동계 모각코를 마무리하며ADsP 자격증 취득모각코 활동 지원비로 교재를 구매할 수 있다고 하여, 자격증 취득을 위한 이론서를 구매했다. 학습을 위한 지원금이 제공되어 좋았다.시험은 지난주 토요일, 2/7일날 응시했다. 채점은 2월 말까지 마무리 된다고
2026 동계 모각코 - 6회차 (계획)
모각코의 마지막 회차 계획은 우선 아래 활동들에 대한 매듭을 짓겠다. 또 6주동안의 모각코 활동을 되돌아 보며 그동안 내가 공부했던 것들에 대해 정리해볼 것이다. ADsP 자격증 취득 (2/7 시험을 응시했다) CS224 Machine Learning with Gra

[도서리뷰] 2026 이기적 SQLD 이론 + 기출문제 구매 후기
최근 영진닷컴 이기적 교재로 ADsP를 공부하며, SQLD 자격증도 취득해볼까 생각을 했고 마찬가지로 영진닷컴 교재로 선택했다. 여러 이유가 있겠지만, ADsP 교재를 구매했던 기준과 같이 적절한 분량과 충분한 연습문제를 풀 수 있다는 점이 마음에 들었다.학습하기에 너

[서평] 관성끊기 (빌 오한론)
빌 오한론, 『관성 끊기 - 반복된 문제를 부수는 최소한의 행동 설계법』우리는 살아가면서 수많은 문제를 마주친다. 물론 그리 중요하지 않거나 쉽게 해결되는 문제도 있지만, 일부 문제는 지속적으로 삶에 등장하여 우리를 괴롭게 만들기도 한다.그런 문제는 보통, 우리의 행동
2026 동계 모각코 - 4회차 (계획)
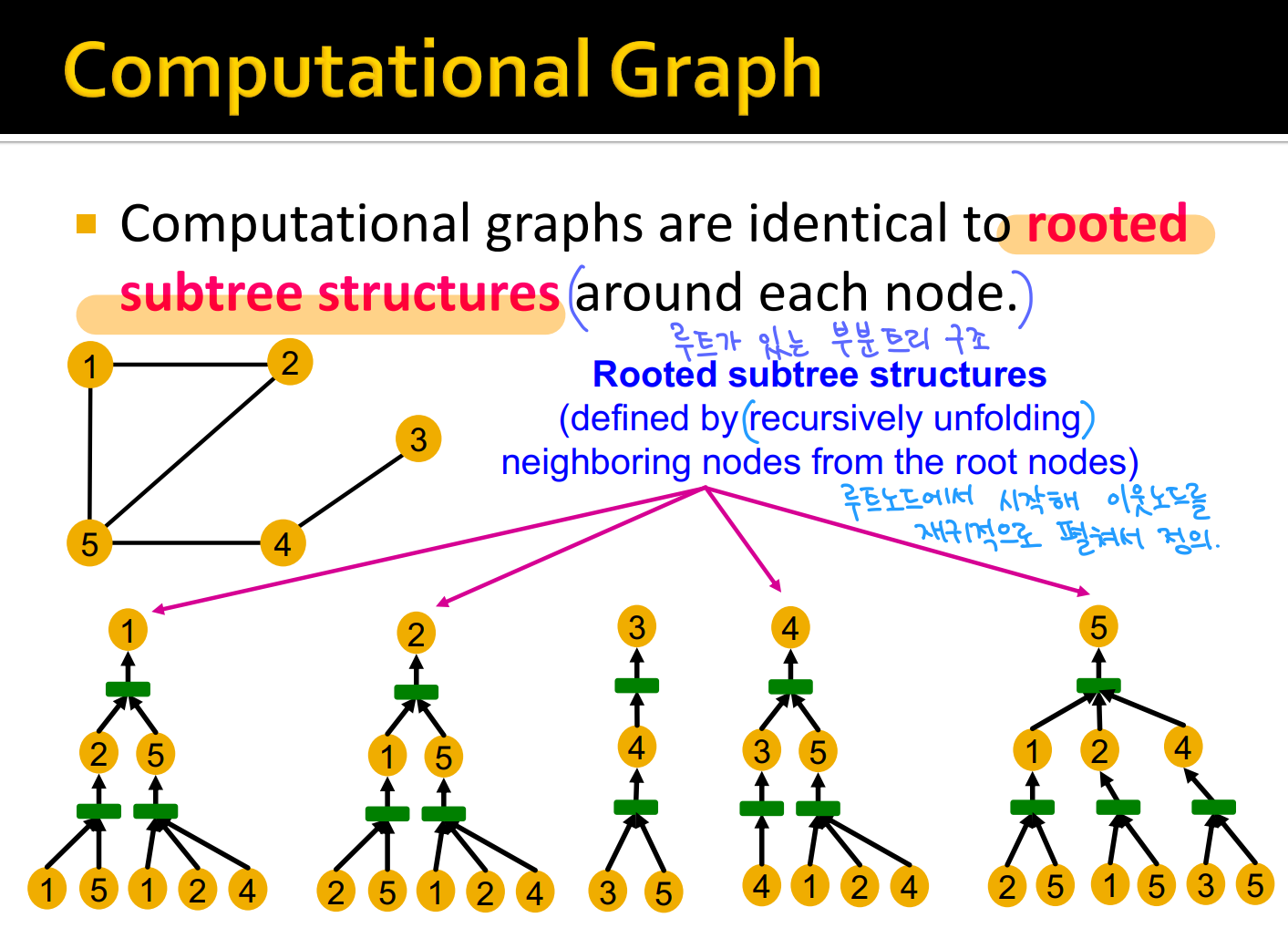
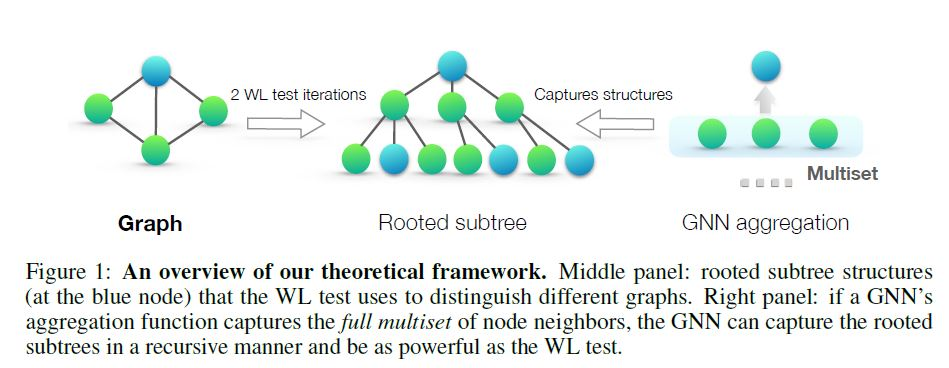
Stanford CS224W 강의 수강 GNN을 위한 증강 기법, 학습 기법 등에 대해서 공부해볼 계획이다. 세부 학습 소주제는 다음과 같이 계획하였다. GNN Augumentation and Training Prediction with GNNs Virtual n

2026 동계 모각코 - 3회차 (결과)
아래 주제들에 대한 학습을 진행하였습니다. 
2026 동계 모각코 - 3회차 (계획)
Stanford CS224W 강의 수강 Graph Neural Networks 및 그래프 기반 표현 학습에 대한 심화 학습을 진행할 계획이다. 학습을 진행할 세부 topic은 아래와 같다. Graph Neural Networks 기본 개념 및 수식적 이해 Geom

2026 동계 모각코 - 2회차 (결과)
Random Walk 전략과 더불어, node2vec 까지 확장하여 인코더로서의 gnn 이전의 접근법에 대해 살펴보았습니다.

2026 동계 모각코 - 2회차 (계획)
학습을 진행할 세부 topic은 아래와 같다. - random walk approaches for node embeddings - embedding entire graphs - Negative Sampling - Node2Vec - Deep Graph Encoders
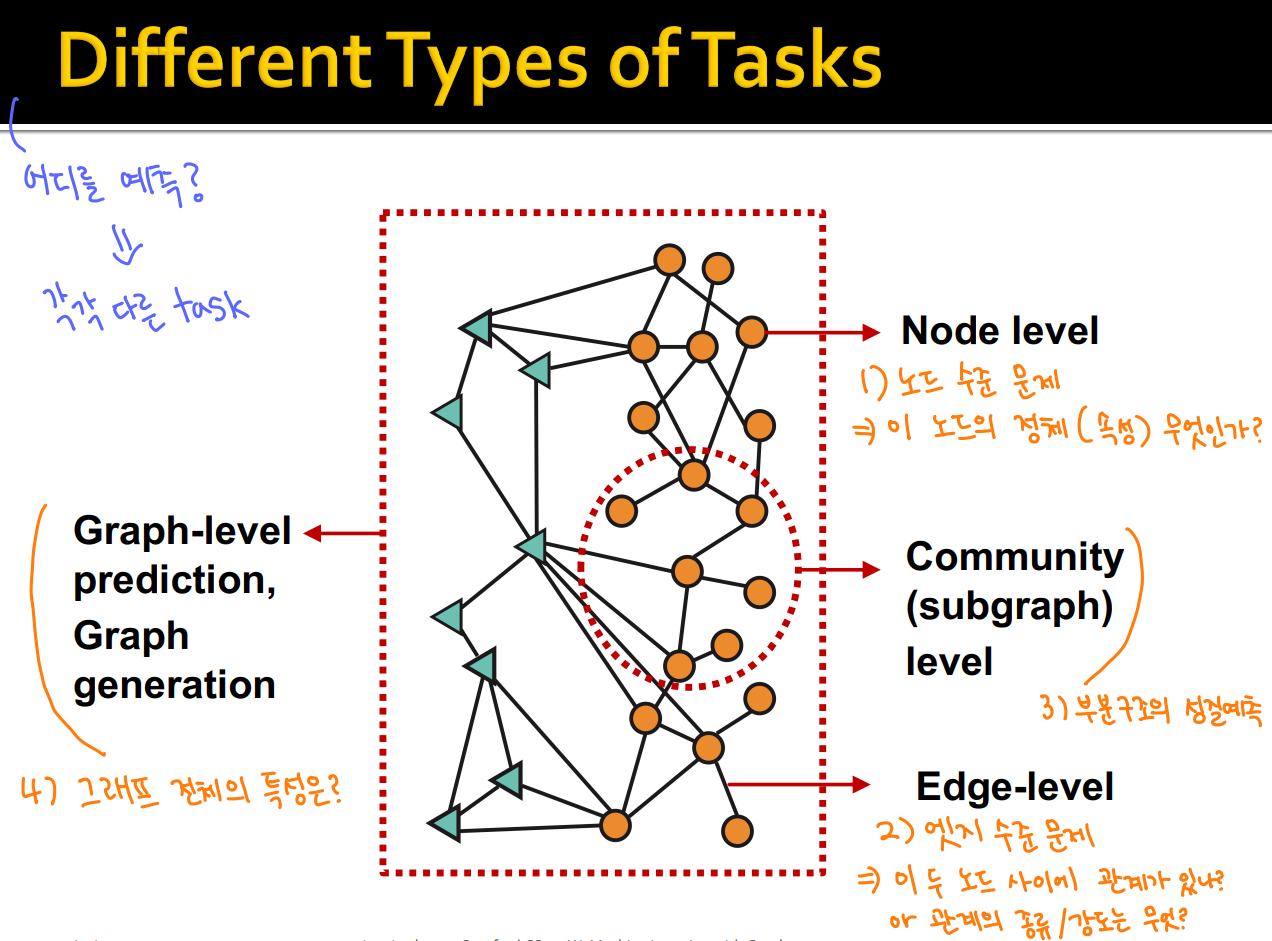
2026 동계 모각코 - 1회차 (결과)
25/12/30 12:00~15:00그래프 기계학습 강의 (Stanford CS224)의 Introduction 부분, Node Embedding 부분에 대한 학습을 진행하였습니다.데이터 분석과 관련하여, ADsP 교재를 통해 데이터 사이언스의 미래와 데이터 사이언티스

2026 동계 모각코 - 1회차 (계획)
1\. Stanford CS224W 강의 수강IntroductionNode Embeddings2\. 데이터 분석 활용
2026 동계 모각코 - 전체 목표
2025~2026 동계 모각코 목표는 다음과 같다.Stanford CS224 강의 수강하고, 그래프 신경망에 개념을 학습할 예정이다.Pytorch, 특히 Pytorch Geometric을 활용한 그래프 기반 신경망 구축 실습을 진행할 계획이다.

[머신러닝(ML)]다중선형회귀(Multiple Linear Regression)-원 핫 인코딩, 다중 공선성, 회귀 모델 평가지수(MAE, MSE, RMSE, R square), 사이킷런(Sklearn) 실습
다중 선형 회귀는 하나의 모델 안에 독립 변수가 여러개일 수 있습니다. 여러 독립변수를 함께 고려한 종속 변수를 예측하기 때문에 단순 선형회귀보다는 더 좋은 성능을 기대할 수 있습니다.

[머신러닝(ML)]단순선형회귀(Simple Linear Regression)-최소 제곱법(OLS), 확률적 경사하강법(SGD), RSS, 사이킷런(Sklearn) 실습
단순 선형 회귀 알고리즘을 학습합니다. 사이킷런(Sklearn) 라이브러리를 사용하여 실습을 진행하고, 최소 제곱법을 손실 함수로 차용하여 해결하는 방법 하나와 확률적 경사하강법(SGD)을 적용시켜 모델을 학습하는 방법 두가지를 살펴봅시다.

[머신러닝(ML)]머신러닝 개요-머신러닝 정의, 종류(지도, 비지도), ML Techniques, 회귀, 분류, 군집화, 연관 규칙
Mitchell의 정의에 의하면 머신러닝은, 작업 T를 수행하기 위한 경험 E로부터 획득한 데이터를 기반으로 모델을 자동으로 구성하여 성능 P를 향상시킬 수 있는 컴퓨터 프로그램이다.

[판다스(Pandas)]그룹화-groupby(), get_group(), 그룹화 후 연산
동일한 값을 가진 것들끼리 뭉쳐서 계산을 쉽게 할 수 있습니다. 그룹화 문법을 공부해봅시다.

[판다스(Pandas)]데이터 수정-컬럼 추가/삭제/수정, Row(행) 추가/삭제/수정, 컬럼 순서 변경, 컬럼 이름변경
데이터프레임의 컬럼과 row(행)을 수정, 삭제, 추가하는 방법을 알아봅시다.