상계와 하계의 여러 가지 성질
상계(supremum)와 하계(infimum)의 여러 가지 성질을 알아보고, 단조 성질(monotone property)을 증명해보자.
다변수 함수의 연쇄 법칙
(Theorem) $f(x,y)$가 미분 가능하고 $x=x(t)$, $y=y(t)$가 $t$에 대하여 미분 가능하면 합성 함수 $f=f(x(t),y(t))$는 $t$에 대하여 미분 가능하며$$\\frac{df}{dt}=\\frac{\\partial f}{\\partia
다변수에서의 미분 가능성
다변수에서는 정의역이 직선이 아니므로 "미분 가능함"을 정의하는데 더 많은 것들이 필요하다. 2차원에서 정의된 함수 $z=f(x,y)$의 모양이 3차원 공간에 펼쳐지게 된다면 편미분을 정의할 때 $xz$와 $yz$ 평면으로 절단해서 절단면에서의 곡선에 대하여 그 기울기
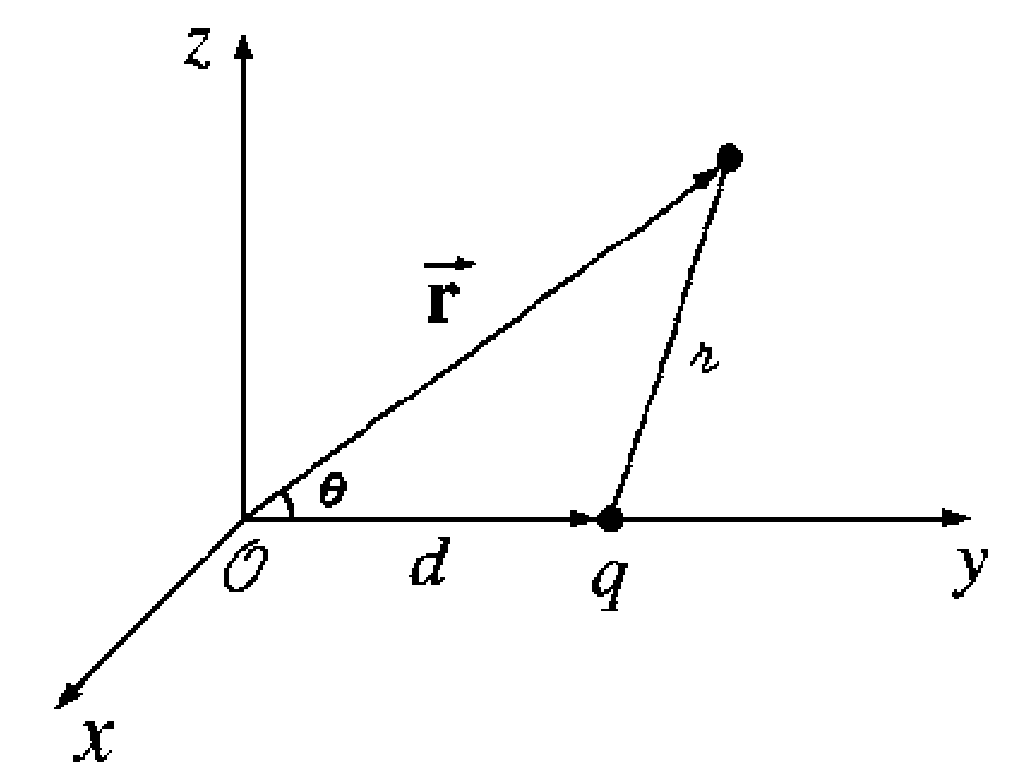
다중극 전개와 원점 의존성
다중극 전개는 좌표계의 원점에 의존한다. 즉, 좌표계의 원점이 바뀌면 다중극 전개 자체가 달라지게 된다. 이를테면, 전하 $q$가 원점에 있을 때, 전기 퍼텐셜은 $$ V(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\frac{q}{r} $$
편미분의 정의와 연속
2차원 평면 좌표계, 즉 $\\mathbb{R}^2$에서의 편미분(partial derivative)에 대하여 알아보기 전에, 우선 $\\mathbb{R}^2$에서 함수의 수렴 및 연속이 어떻게 정의되는지 알아보자.
상극한과 하극한의 대소 관계
앞에서 임의의 수열에 대하여 그것의 상극한과 하극한에 수렴하는 부분 수열이 언제나 존재한다고 했다. 상극한, 하극한 및 수렴하는 수열 사이에는 그 밖의 여러 가지 관계가 성립한다.
상극한과 하극한
수열의 상극한(limit supremum)과 하극한(limit infimum)은 확장된 실수(extended real numer)에서 정의되는 수열에 대하여 그 "경계"의 극한이다.
삼각 부등식
(Theorem) (삼각 부등식) 임의의 복소수 $z_1$, $z_2$에 대하여 다음이 성립한다: $|z_1+z_2| \le |z_1|+|z_2|$.
수열의 비교 정리
수렴하는 두 수열이 $N$번째 항 이상에서 대소 관계를 유지한다면 그 극한들끼리도 대소 관계를 유지한다. (Theorem) (수열의 비교 정리) 수렴하는 두 수열 $\{an\}$과 $\{bn\}$을 생각하자. 만약 어떤 자연수 $N$에 대하여
최소 상계(sup) 및 최소 상계 성질 (Least upper bound property)
(Definition) 실수의 부분 집합 $R$에 대하여 $R$의 임의의 원소 $r$이 언제나 $r\le M$인 실수 $M$이 존재하면 $M$은 $R$의 "상계(upper bound)"이다. 만약 $A$가 $R$의 상계이고 $A$보다 더 작은 상계가 존재하지 않는다면
수열에서 수렴과 발산의 정의
(Definition) 수열 $\{a_n\}$이 임의의 $\varepsilon >0$에 대하여 대응되는 자연수 $N$이 있어서 $ n>N \Rightarrow |a_n - L| < \varepsilon$ 을 만족하면 $\{a_n\}$이 $L$에 "수렴한다"라고 한다.
실수 체계
실수 체계(real number system)의 정의는 크게 세 가지 단계로 이루어질 수 있는데, 대수적 성질, 순서(ordering) 공리, 그리고 완비성(completeness)이다.
비교 판정법 (Comparison tests)
(Theorem) (비교 판정법; The comparison test) 무한 급수 $\sum a_n$, $\sum c_n$, $\sum d_n$이 각각 음이 아닌 항들의 합으로만 구성되어있다고 가정하자. 그리고 어떤 자연수 $N$에 대하여 $n\ge N$일 때
무한 급수
무한 급수 $$\\sum\_{n=1}^\\infty a_n = a_1+a_2+a_3+\\cdots $$가 $L$에 "수렴한다"는 것은 임의의 $\\varepsilon > 0$에 대하여 다음을 만족하는 자연수 $N$이 존재한다는 뜻이다: 임의의 자연수 $n > N$에 대
연쇄 법칙 (Chain rule)
(Theorem) 만약 $f(u)$가 $u$에 대하여 미분 가능하고, $u=g(x)$이며 $g(x)$는 $x$에 대하여 미분 가능하다면 합성 함수 $(f\circ g)(x)=f(g(x))$는 $x$에 대하여 미분 가능하고, 이때 $$ (f\circ g)'(x)=f'(
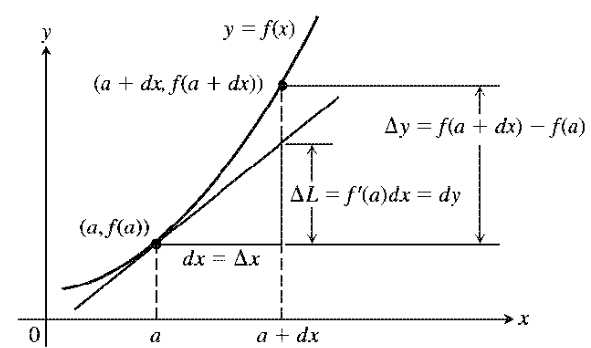
선형 근사와 미분소
직선의 방정식은 $y = ax + b$이다. 또는 보다 일반적인 표현으로 임의의 직선은 $ax+bx+c=0$로 쓸 수 있다.이를 미분을 사용하여 표현해보자면, 모든 "미분 가능한" 곡선 $y = f(x)$은 임의의 $x=x_0$에서의 접선, 즉 기울기 $f'(x_0)$
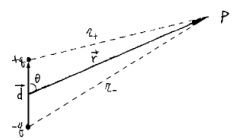
전기 쌍극자
쌍극자(dipole)는 두 개의 반대 부호의 전하가 약간 떨어진 상태로 같이 있는 분포를 말한다. 이를테면 $d$ 만큼 떨어진 $+q$와 $-q$ 전하가 있다고 하자.그러면 점 $P$에서의 전기 퍼텐셜은 다음과 같다:$V(\\vec{r}) = \\frac{1}{4\\p

