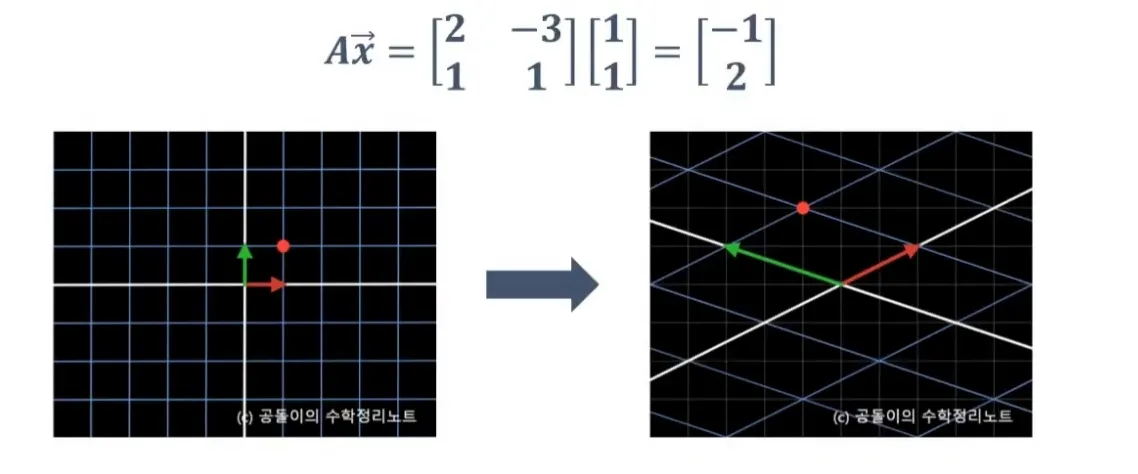
Linear Transformation & Matrices
변환(Transformation): 입력으로 벡터를 받아 다른 벡터를 출력하는 함수(function).$$T(\\vec{v}) = \\vec{w}$$의 형태로, 벡터 v를 벡터 w로 이동시키는(Transform) 함수다.벡터를 “화살표”가 아닌 “화살표의 끝점(poi
등차수열(arithmetic sequence), 등비수열(geometric sequence)
$$a_n = a_1 +(n-1)d\\S_n= a_1+a_2+...+(a_1+(n-1)d)$$역순끼리 더하면$$S_n= a_1+(a_2+d)+...+(a_1+(n-1)d)\\S_n= (a_1+(n-1)d)+(a_1+(n-2)d) +... +a_1\\2S_n = (2a_
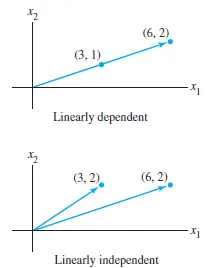
선형결합(Linear Combinations), 스팬(Span), and 기저 벡터(Basis Vector)
단위벡터(unit vector): 크기가 1인 벡터$\\hat{i} = (1,0)$ → 2차원 공간 기준$\\hat{j} = (0,1)$2차원 벡터 (3,−2)는 두 개의 스칼라(3, -2)로 표현됨.3은 x축 방향 단위벡터 $\\hat{i}$를 3배로 늘린 것2는 y
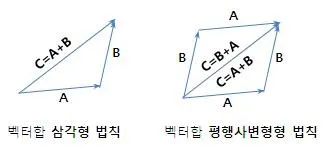
1. 벡터
선형대수(linear algebra)의 가장 기본이 되는 개념은 벡터(vector)다.벡터에 대해 이해하는 관점은 여러 가지가 있으며, 크게 세 가지 시각으로 나눌 수 있다.벡터는 공간 속의 화살표(arrow in space)로 생각한다.벡터를 정의하는 두 가지 요소는
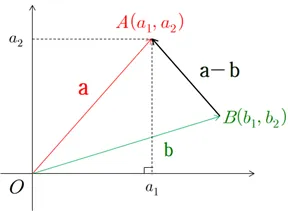
벡터의 내적 (inner product)
두 벡터 a = (a1, a2, a3)과 b = (b1, b2, b3)의 내적은 다음과 같이 정의된다.$$a \\cdot b = a_1b_1+a_2b_2+a_3b_3$$위 그림에서 a-b는 두 벡터의 끝점을 연결하며 이는 삼각형의 변이 된다. a, b, c 세 변을 가
적분을 이용한 구의 부피 구하기
구의 방정식은$$x^2 +y^2 +z^2 = r^2$$특정 높이에서 자른 단면에서 구의 방정식은 $$y^2 + z^2 = r^2 - x^2 ~(단, x는 상수)$$이며 반지름이 $\\sqrt{r^2-x^2}$인 원의 방정식이 된다. 자른 단면의 반지름 $p = \\sq
부분 적분법
곱의 미분을 다시 적분하여 얻어진 결과두 함수 u(x), v(x)를 미분하면 곱의 미분에 의해 다음과 같다.$$\\\\frac{d}{dx}u(x)v(x)=u'(x)v(x) + u(x)v'(x)$$다시 x에 대해 적분하면$$\\int\\frac{d}{dx}uvdx = \
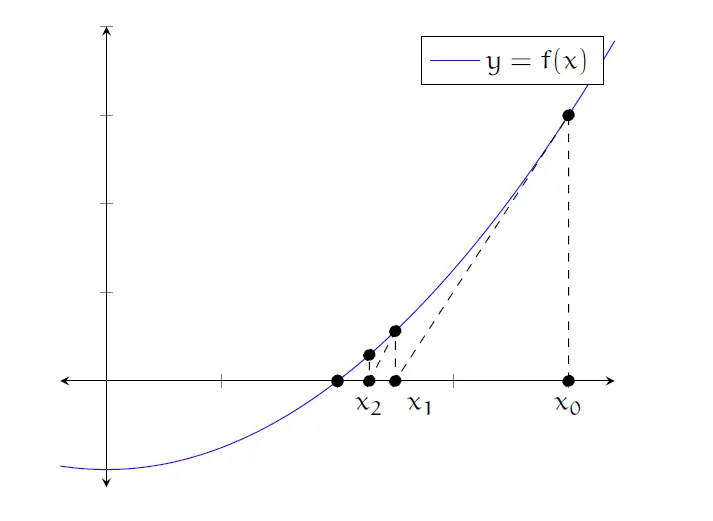
뉴턴 방법 (Newton's Method)
뉴턴 방법은 방정식의 해를 수치적으로 근사해서 구하는 것이다. 즉, 그래프가 x축과 만나는 점을 구하는 것이다.출발점 x0에 대해서 다음과 같이 정의할 수 있다. $$(x_0, f(x_0))의~접선\\y = f(x_0) + f'(x_0)(x-x_0)$$접선이 x축을 지
연쇄법칙
$$z = f \\circ g(x) = f(g(x)) = f(x)g(x)\\ z' =f'(x)g'(x) = \\frac{dz}{dx}$$$$\\ u = g(x)일~때,\\f'(u) = \\frac{f변화량}{u변화량} = \\frac{fu}{du}$$$$\\ g'(x)
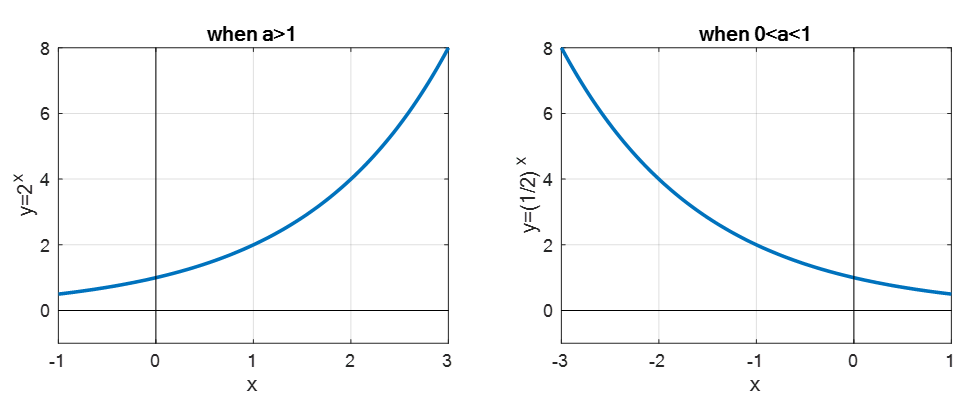
지수함수
a가 양의 상수일 때 정의역이 실수인 함수$$$y = a^x$$$지수함수 a 값은 무리수인 오일러 수가 많이 사용되며 지수적 성장을 표현한다.$$$e = 2.17828...\\y=e^x=exp(x)$$$지수함수는 a값에 따라 모양이 면한다 0<a<1이면 x가
삼각함수
삼각비 삼각비는 직각삼각형에서 각 변의 비율을 나타낸 것이다. $$ sin \theta = \frac{높이}{빗변} $$ $$ cos \theta = \frac{밑변}{높이} $$ $$ tan \theta = \frac{높이}{밑변} $$ 단위원으로 확장하기 9

K-Means Clustering
비지도 학습(Unsupervised Learning) 기법레이블(정답)이 없는 데이터를 비슷한 것끼리 그룹으로 묶는 알고리즘목표는 각 데이터 x_i와 그것이 속한 클러스터의 중심 c_j 사이의 거리(보토 유클리드 거리)의 제곱합을 최소화하는 것동작 원리1\. K개의
Principal Component Analysis(PCA)
차원 축소 (dimensionality reduction)과 변수 추출(feature extraction) 기법데이터의 분산을 최대한 보존하면서 서로 직교하는 새 축을 찾아 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법변수를 축소함으로써 과적
Ensemble
머신러닝에서 여러 개의 모델을 결합하여 하나의 최종 예측을 만드는 기법을 말한다.앙상블을 사용하는 이유단일 모델은 데이터의 일부 패턴만 잘 잡을 수 있다.여러 모델의 예측을 종합해 Overfitting을 줄이고 새로운 데이터에 대한 예측을 더 안정적으로 할 수 있다.모

Cross Validation & Hyper Parameter
과적합모델이 학습 데이터에만 과도하게 최적화된 현상. 일반화된 데이터에서 모델의 예측 성능이 떨어짐Holdout데이터를 학습용, 테스트용 두 가지로 나누는 것여전히 과적합의 가능성이 있음K-fold Cross Validation전체 데이터셋을 랜덤하게 섞은 후 K개의
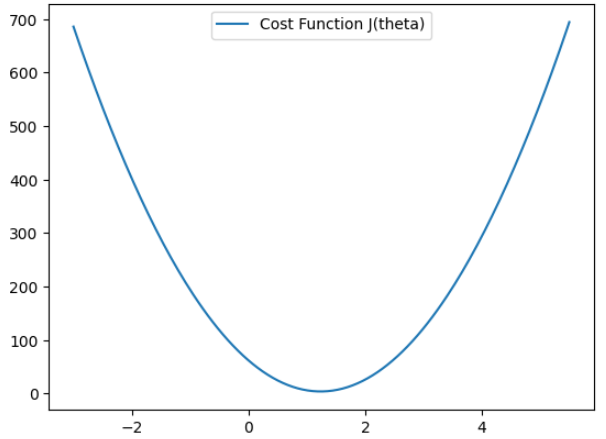
Logistic Regression
로지스틱 회귀는 독립 변수들을 사용해 사건이 발생할 확률을 예측하는, 분류용 통계·머신러닝 모델이다.비용함수모델이 얼마나 잘 예측하고 있는지를 수치로 표현하는 기준데이터 전체를 보고, 예측값과 실제값의 차이를 하나의 숫자로 요약한 것가설함수 (Hypothesis)를 아

파이프라인
Jupyter Notebook을 사용하면 데이터 전처리, 하이퍼 파리미터 튜닝 등 여러 반복을 진행하다보면 혼란을 야기할 수 있다.Sklearn에는 Pipeline을 이용해 여러 단계 (전처리 -> 학습 -> 예측)을 하나의 객체로 묶을 수 있다. 코드와 노트의 일관성
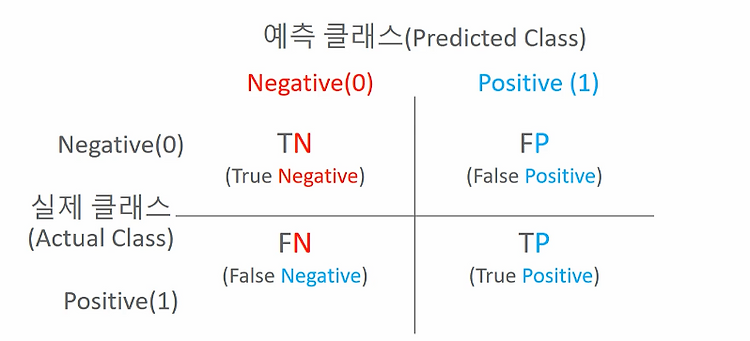
모델 평가
분류 모델의 평가분류 모델은 다음과 같은 항목을 이용해 평가한다.정확도 (Accuracy)오차행렬 (Confusion Matrix)정밀도 (Precision)재현율 (Recall)F1 ScoreROC AUC위의 오차행렬 (Confusion Matrix)을 이용해 정확도
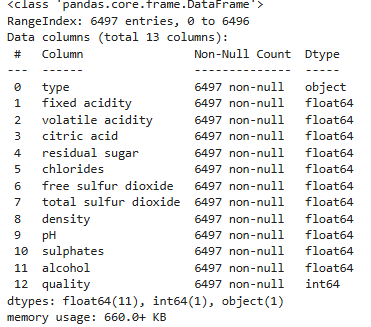
와인 분류하기
이번 코드의 경우 시간 간격을 두고 작업하여 변수명, 코드작성방법이 일정하지 않을 수 있다. 너그러이 바라봐주시길 바라며 추후 기회가 된다면 업데이트하도록 하겠다.데이터셋은 와인의 성분과 quality 점수를 제공한다. 이를 이용해 와인 type을 예측하는 모델과 qu

