이 글은 랭체인으로 LLM 기반의 AI 서비스 개발하기 도서를 읽고 개인 정리한 글입니다. 모르는 부분을 중심으로 TIL을 작성했습니다.파인튜닝과 전이학습은 모두 기존에 학습된 모델을 활용하여 새로운 작업을 수행하기 위한 방법이지만 접근 방식과 적용 범위에 차이가 있다

Gram-Schmidt는 서로 직각도 아니고 길이도 제멋대로인 벡터들을 서로 직각인(= 직교) 기준 벡터들로 바꾸는 방법이다.직교 벡터가 훨씬 계산이 쉽고, 정사영도 정확히 되고 수학적으로 안전한 방식이기 때문이다.v1 방향으로 비쳐긴 그림자를 빼면 진짜 새로운 방향

정사영(Orthogonal Projection)은 벡터를 다른 벡터 방향으로 그림자처럼 내려보낸 것을 말한다. 예를 들어, 우리가 벡터 u와 v 두 개를 갖고 있다고 하자. 그런데 u를 v 방향으로 그림자처럼 내리고 싶다고 하면, 여기서 그 그림자 벡터가 바로 정사영

내적은 두 벡터가 얼마나 같은 방향을 향하고 있는지를 숫자로 말한 것이다. 우리는 내적을 공부할 때 서로 얼마나 같은 방향인지를 잘 살펴보고, 성분끼리 곱해서 더해야 한다.내적(Inner Product)과 도트 곱(Dot Product) 그리고 스칼라 곱(Scalar

1. 대각화

고유값을 구했을 때 어떤 고유값이 한 번만 나올 수도 있고 여러 번 반복될 수도 있다. 여기서 대수적 중복도(Algebraic Multiplicity)는 그 고유값이 몇 번 나왔는지를 말한다.특성 방정식을 계산할 때 Sarrus 법칙이나 여인수 전개를 사용하는 것도 좋

보통은 행렬 A가 벡터 x를 바꾸면, 벡터의 방향과 길이도 바뀐다. 그런데 특정한 벡터들은 방향이 안 바뀌고 길이만 λ배 바뀐다. 이렇게 방향이 안 바뀌는 벡터를 고유 벡터(Eigenvector)라고 하며, 이때 곱해진 숫자 λ를 고유값이라 한다.고유값을 고유치라고도

1. 선형 방정식과 선형 변환 선형 방정식은 우리가 흔히 보는 식인 이다. 여기서 A는 행렬, x는 입력 벡터, y는 출력 벡터이다. 이걸 함수로 보면 입력 x를 넣으면 결과 y가 나오는 것이라 볼 수 있다. 그래서 이걸 변환(Transformation) 또는 사상

우리는 평면에서 (3, 2)라는 점을 보통 x축 1칸, y축 1칸 기준으로 본다. 나만의 새로운 축을 만들어서 그 축을 기준으로 벡터를 표현하면 좌표가 달라지는 것은 당연하다. 여기서 그 기준이 되는 축이 바로 기저(Basis)이다.기저 B가 표준 기저(가장 기본적으로

이상 현상(Abnomaly) : 데이터를 입력, 수정, 삭제하는 과정에서 의도치 않게 일관성이 깨지는 현상이상 현상에는 삽입 이상, 갱신 이상, 삭제 이상이 존재한다.삽입 이상은 테이블에 데이터를 삽입할 때 의도하지 않은 정보까지 삽입해야 하는 현상을 말한다.갱신 이상

모델링(Modeling) : 현실 세계를 대상으로 일종의 모델을 만드는 것모델(Model) : 현실 세계의 사물 혹은 개념을 구성요소로 나누고, 이를 일정하게 도식화한 것모델링에서 중요한 것은 도식화하는 방법과 약속된 표기법을 따라야 한다는 것이다.모델링을 하는 이유

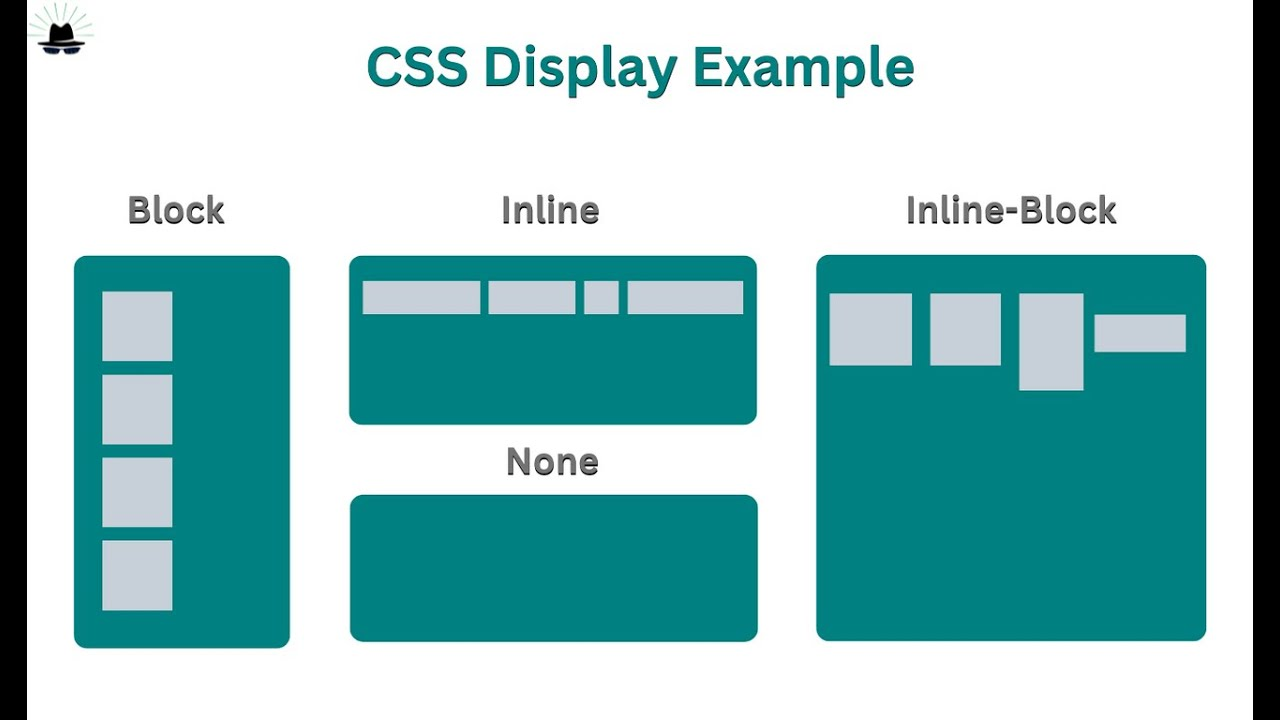
CSS는 Cascading Style Sheets로, HTML로 만든 웹 페이지에 디자인(스타일)을 입히는 것이다. HTML로 뼈대를 만든다면, CSS는 그 위에 옷을 입히는 것이다.Cascade는 '폭포처럼 쏟아지는 물'이라는 의미가 있다. 결국 계속 이어진 두 가지

1. HTML HTML은 (Hyper Text Markup Language로, 웬사이트 표시를 위해 개발된 마크업 언어이다. 문서의 내용을 태그로 사용하여 구성한다. Hyper Text는 하이퍼링크를 통해 한 문서에서 다른 문서로 즉시 접근할 수 있도록 하는 것이다

기저(Basis) : 해당 공간의 기준점이 되는 부분이다.하나의 벡터공간에 기저가 될 수 있는 집합은 여러 개가 있을 수 있다. 그러나 그 벡터공간의 기저를 이루는 집합들의 각 원소의 개수는 모두 같다.차원은 기저의 개수와 동일하다.표준 기저(Standard Basis

벡터공간은(Vector Space)은 영벡터를 포함해야 하며, 덧셈과 스칼라 곱을 자유롭게 할 수 있어야 한다.벡터공간 V에서 V 자신과 {0}은 V의 부분공간들 중 하나이다. 이러한 부분공간을 V의 자명한 부분공간(Trivial Subspace)라고 하며, 특히 {0

벡터의 내적은 스칼라 값 1개가 나오지만, 벡터의 외적은 방향과 크기를 가진 또 다른 새로운 벡터를 만들어 낸다.외적은 교환 법칙이 성립하지 않는다. u × v가 0이라면 u, v가 같은 방향이거나 평행한 경우이다. 외적 벡터가 존재하지 않는다.외적과 내적에 대해서 다

동차선형방정식 Ax = b는 Det(A)이 0이 아닐 때, 자명한 해를 갖는다.여인수들로 구성된 행렬을 여인수 행렬(Cofactor Matrix)라고 하며, 이 여인수 행렬의 전치행렬을 수반행렬(Adjoint Matrix of A)라고 한다. 기호로는 adj(A)로 나

각 행에서 원소를 하나씩 고르되, 열이 서로 겹치지 않게 고른다.기본 곱에 부호를 붙이면 행렬식(Determinent)가 된다.전도 : 어떤 큰 자연수가 작은 자연수보다 먼저 나타나 있을 때 전도되었다고 말한다.전도수 : 하나의 순열에서 나타나는 전도의 총 개수를 전도

벡터의 내적은 벡터 두 개를 곱해서 하나의 숫자(스칼라)를 만들어내는 연산이다. 직각(수직) 판별 및 정사영 등에 사용된다. 내적은 실수값임을 잊지 말아야 한다.직교(Orthogonal)는 벡터들이 서로 수직이라는 것을 의미하며, 결국 내적이 0이 된다.두 벡터가 이루

선형결합(일차결합)은 벡터들을 어떤 스칼라(수)로 곱하고 더한 것을 말한다. 같은 차원이 여러 벡터들을 실수배하여 더한 식이다.벡터(선형)방정식 : 선형방정식의 계수를 열벡터로 표현하고, 벡터 b를 선형결합으로 나타내는 것을 말한다.선형방정식의 해를 구한다는 것은 열벡